Automatic recognition of sleep spindles in EEG via radial basis support vector machine based on a modified feature selection algorithm

Abstract

This paper presents an application of a radial basis support vector machine (RB-SVM) to the recognition of the sleep spindles (SSs) in electroencephalographic (EEG) signal. The proposed system comprises of two stages. In the first stage, for feature extraction, a set of raw amplitude values, a set of discrete cosine transform (DCT) coefficients, a set of discrete wavelet transform (DWT) approximation coefficients and a set of adaptive autoregressive (AAR) parameters are calculated and extracted from signals separately as four different sets of feature vectors. Thus, four different feature vectors for the same data are comparatively examined. In the second stage, these features are then selected by a modified adaptive feature selection method based on sensitivity analysis, which mainly supports input dimension reduction via selecting the most significant feature elements. Then, the feature vectors are classified by a support vector machine (SVM) classifier, which is relatively new and powerful technique for solving supervised binary classification problems due to it’s generalization ability. Visual evaluation, by two electroencephalographers (EEGers), of 19 channel EEG records of six subjects showed that the best performance is obtained with an RB-SVM providing an average sensitivity of 97.7%, an average specificity of 97.4% and an average accuracy of 97.5%.

1 Introduction

Sleep spindles (SSs) are transient sleep electroencephalographic (EEG) waveforms. Along with K-complexes, they are the hallmarks of stage-2 sleep. The incidence of SSs is the highest in the course of the sleep episode [1]. Furthermore, spindles can be used to analyse sleep microstructure [2, 3]. SS activity has been reported to reside between 10-Hz and 16-Hz oscillations and lasting from 0.5 s to 3 s [4–6]. There is now reliable evidence that spindle activity is a consequence of the membrane hyperpolarisation of thalamocortical and cortical neurons. During sleep, periodic bursts of action potentials converge back to neurons of the reticular thalamic nucleus, which facilitates and synchronises the rhythmic oscillations. These bursts are then transferred to the cortex where they induce excitatory postsynaptic potentials and, thereby, generate SSs [7, 8].

Sleep staging is one of the most important procedures for diagnosis in psychiatry and neurology. The sleep staging of EEG data, however, is liable to be subjective since it depends on the medical expert’s skill and requires much labour. Visual spindle detection of all-night EEG recordings is time consuming and tedious because there are a lot of spindles in one all-night recording. An automatic diagnosis system must, therefore, be developed to reduce medical experts’ labour and realise an objective—the quantitative diagnosis of sleep EEG data.

Many automated methods for spindle detection have been proposed in the literature [9–14]. The earliest is based on hardware [15, 16]. Moreover, some methods are based on a kind of template matching. This makes it difficult to cope with the large variation of EEG data, such as fluctuations of the frequency pattern and the differences between individuals. The method of detecting the SSs in EEG data must, therefore, be robust to a variation of patterns.

We also observed that feature extraction methods in such applications can be divided into three subgroups, such as raw data vectors extraction, transformation methods and characteristic parameter estimation methods. Therefore, we comparatively examined four different feature sets based on these kinds of extraction methods.

In the approach proposed here, first, four different feature sets are extracted from the same EEG data. Then, by using an adaptive feature selection technique, which is explained in detail in Sect. 2, the significant features are selected. Thus, the dimension of the feature vector is reduced to be much smaller than the original dimension but without loss of information. After that, successive sweeps are fed to the support vector machine (SVM) classifier, which maps the feature vector onto a single binary output {−1, 1 } [17, 18]. Thus, the proposed SVM-based method employs a classification procedure that would display good classification performance whilst being efficient in terms of memory and time requirements due to dimensionality reduction.

In Sect. 2, the SVM classifier and adaptive feature selection method based on SVMs are formulated. In Sect. 3, the data acquisition and application of our novel system to real data are proposed. The results and discussion are reported in Sect. 4.

2 Support vector machines and feature selection method

This section describes in detail the methods used in the proposed automated recognition system. The theory of SVM is formulated in Sect. 2.1. Section 2.2 introduces the formulation of an adaptive feature selection method based on SVMs in detail. A block diagram of recognition system is shown in Fig. 1.

Fig. 1

Block diagram of the recognition system

2.1 Support vector machines

Using SVMs is a relatively new and powerful technique for solving supervised classification problems and is very useful due to its generalisation ability. In essence, such an approach maximises the margin between the training data and the decision boundary, which can be cast as a quadratic optimisation problem. The subsets of patterns that are closest to the decision boundary are called support vectors. The architecture of the SVM is shown in Fig. 2.

Fig. 2

Architecture of the SVM. Here, K(.) is a kernel function, M is the number of support vectors and P is the input dimension

For a linearly separable binary classification problem, the construction of a hyperplane w^Tx+b=0 so that the margin between the hyperplane and the nearest point is maximised, can be posed as the following quadratic optimisation problem [19]:

$$\mathop {\min }\limits_{\mathbf{w}} \frac{1}{2}({\mathbf{w}}^{\text{T}} {\mathbf{w}})$$

(1)

subject to:

$$ d^i (({\mathbf{w}}^{\text{T}} {\mathbf{x}}^i ) + b) \geq 1\;{\text{with}}\;i = 1, \ldots ,N $$

(2)

where dⁱ∈{−1, 1 } stands for the ith desired output, xⁱ∈R^P stands for the ith input sample of the training data set {xⁱ, dⁱ} ^N_i=1 . Equation 1 forces a rescaling on (w, b) so that the point closest to the hyperplane has a distance of $\frac{1}{{\left\| w \right\|}}$ [19]. Maximising the margin corresponds to minimising the Euclidean norm of the weight vector. Often, in practice, a separating hyperplane does not exist. Hence, the constraint shown in Eq. 2 is relaxed by introducing slack variables ξ _i ≥0, i=1,..., N. The optimisation problem now becomes as follows (for a user-defined positive finite constant C):

$$\mathop {\min }\limits_{{\mathbf{w}},\xi } \frac{1} {2}({\mathbf{w}}^{\text{T}} {\mathbf{w}}) + C\sum\limits_{i = 1}^N {\xi _i } $$

(3)

subject to:

$$ d^{i} (({\mathbf{w}}^{{\text{T}}} {\mathbf{x}}^{i} ) + b) \geqslant 1 - \xi _{i} $$

(4)

$$ \xi _i \geq 0\;{\text{with}}\;i = 1, \ldots ,N $$

(5)

The constant C controls the tradeoff between the complexity of the machine and the number of non-separable points; it may, therefore, be viewed as a form of “regularisation” parameter.

By introducing Lagrange multipliers α _i and, using the Karush-Kuhn-Tucker theorem of optimisation theory, we can pose the equivalent dual optimisation problem [20]:

$$\mathop {\max }\limits_{\alpha _i } \sum\limits_{i = 1}^N {\alpha _i - \frac{1} {2}\sum\limits_{r,i = 1}^N {\alpha _r \alpha _i d^r d^i (({\mathbf{x}}^r )^{\text{T}} {\mathbf{x}}^i )} } $$

(6)

subject to:

$$ 0 \leq \alpha _i \leq C\;{\text{with}}\;i = 1, \ldots ,N $$

(7)

$$ \sum\limits_{i = 1}^N {\alpha _i d^i = 0} $$

(8)

The solution is given by:

$$ {\mathbf{w}} = \sum\limits_{i = 1}^N {d^i \alpha _i {\mathbf{x}}^i } $$

(9)

The non-zero α _i s correspond to the so-called support vectors xⁱ that help to define the boundary between the two classes. All other training examples with corresponding zero α _i values are now rendered irrelevant and automatically satisfy the constraint in Eq. 4 with ξ _i =0. The hyperplane decision function can be written for the vector x as follows:

$$f({\mathbf{x}}) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^N {d^i \alpha _i ({\mathbf{x}}^{\text{T}} {\mathbf{x}}^i ) + b} } \right)$$

(10)

To allow for more general decision surfaces, the inner product 〈x, xⁱ〉=x^Txⁱ can simply be replaced by a suitable kernel function K(·, ·). Hence, the objective function to be maximised can now be written as:

$$ \sum\limits_{i = 1}^N {\alpha _s - \frac{1} {2}\sum\limits_{r,i = 1}^N {\alpha _r \alpha _i d^r d^i K({\mathbf{x}}^r ,{\mathbf{x}}^i )} } $$

(11)

with the constraint equations Eqs. 7 and 8 remaining unchanged. The decision function for the vector x then becomes:

$$ f({\mathbf{x}}) = \operatorname{sgn} \left( {\sum\limits_{i = 1}^N {d^i \alpha _i K({\mathbf{x}},{\mathbf{x}}^i ) + b} } \right) $$

(12)

The α _i s are determined from Eqs. 11, 7 and 8. The bias parameter b is determined from Eq. 10 by using two arbitrary support vectors from known but opposite classes.

By replacing the inner products with kernel functions, the input data are mapped to a higher dimensional space. It is, then, in this higher dimensional space that a separating hyperplane is constructed to maximise the margin. In the lower dimensional data space, this hyperplane becomes a non-linear separating function.

In the implementations, we construct a radial basis support vector machine (RB-SVM) by using a radial basis function as the kernel function in the SVM as follows:

$$ K({\mathbf{x}},{\mathbf{x}}^s ) = \exp \left( { - \frac{{\left\| {{\mathbf{x}} - {\mathbf{x}}^s } \right\|^2 }} {{2\sigma ^2 }}} \right) $$

(13)

where σ ²=1.

Thus, the decision function becomes:

$$ f({\mathbf{x}}) = \operatorname{sgn} \left( {\sum\limits_{s = 1}^S {d^s \alpha _s \exp \left( { - \frac{{\left\| {{\mathbf{x}} - {\mathbf{x}}^s } \right\|^2 }} {{2\sigma ^2 }}} \right) + b} } \right) $$

(14)

2.2 Perturbation-based statement of the feature selection method

In classification problems, feature extraction is one of the most important stages. Because the dimension of the input vector directly affects the performance of the SVM classifier, the reduction of the input dimension not only reduces the computing time, but it also increases the performance of the system. In this study, we proposed a qualitative method, which is stated by using perturbation method and adapted as a saliency metric to the SVM, for selecting the best features. Similar analysis which has motivated us for SVMs is done for multilayer perceptron networks [21].

The mappings in the SVM are R^P→R with continuous and differentiable output $y({\mathbf{x}}) = {\sum\limits_{i = 1}^N {d^{i} \alpha _{i} K({\mathbf{x}},{\mathbf{x}}^{i} ) + b} },$ where x∈R^P. Let us consider an SVM classifier which is assumed to perform a non-linear, differentiable mapping Γ:R^P→R, y=Γ(x), where y (1×1) and x (P×1) are the output and input vectors, respectively. In further discussion, we assumed that some certain inputs carry no or little relationship to the output. Therefore, they can be discarded. The main aim here is to reduce the original dimension of the input vector, x. Thus, a smaller SVM network can be modelled without a loss of accuracy.

Let y:R^P→R with a function y. Suppose xⁱ∈Ω, where Ω is an open set, for contributing to the differentiability of y at xⁱ. Since y is differentiable at xⁱ, we can expand y(xⁱ+Δx) into the Taylor series for linearisation as follows:

$$ y({\mathbf{x}}^i + \Delta {\mathbf{x}}) = y({\mathbf{x}}^i ) + \nabla ^{\text{T}} y({\mathbf{x}}^i )\Delta {\mathbf{x}} + h(\Delta {\mathbf{x}}) $$

(15)

where $\nabla y({\mathbf{x}}^i ) = \left[ {\begin{array}{*{20}c} {\frac{{\partial y}}{{\partial x_1 }}} \\ {\frac{{\partial y}} {{\partial x_2 }}} \\ \vdots \\ {\frac{{\partial y}}{{\partial x_P }}} \\ \end{array} } \right]$ is the gradient vector, h(Δx) represents the high-order terms and:

$$ \mathop {\lim }\limits_{\Delta {\mathbf{x}} \to 0} \frac{{h(\Delta {\mathbf{x}})}} {{\left| {\Delta {\mathbf{x}}} \right|}} = 0 $$

(16)

Let us assume now that the SVM network with input x is perturbed by Δx→0. After the perturbation procedure, the first term of Eq. 15 is fixed and the third term h(Δx) is vanished in accordance with Eq. 16. Consequently, the only remaining component in Eq. 13 is ∇^Ty(xⁱ)Δx. Here, the multiplier Δx is also vanished by assuming that to be a normalisation factor. Thus, the vector ∇^Ty(xⁱ) provides the first-order directional information about the non-zero displacement, y(xⁱ+Δx)−y(xⁱ).

Now the aim is to evaluate the displacements in the result of the perturbation procedure over the entire training set, T={x¹, x²,..., x^N}.

Let us measure the output changes between y(xⁱ) and y(xⁱ+Δx) caused by perturbation for training vectors xⁱ∈T. Here, the measured displacements are for small and identical Δx for j=1, 2,..., N. After projecting these changes to the input space R^P, we ask whether all P dimensions of input vectors contribute to the output changes or not. If the input changes that are causing output perturbations for variable x^j does not contribute to the output changes y(x^j+Δx), it means that the output is constant in x^j.

Consequently, if the output is insensitive to the jth variable of input vector x∈R^P, the jth variable of the gradient vector can be discarded. The insensitivity to the jth variable should hold for the entire training set T. Thus, the jth element can be zeroed for ∇^Ty(xⁱ), n=1, 2,..., N. On the other hand, in real-world problems, qualitative methods other than zeroing are necessary to rank the significance of each individual element of input vector over the training set. Such a method is formulated and an algorithm is presented in the following section.

2.3 Saliency analysis

Belue and Bauer [22] firstly proposed the saliency analysis in a derivative-based sense and they have also expressed the analysis in detail for the multilayer perceptron networks [23]. In derivative-based saliency analysis, the saliency metric is calculated by evaluating the sensitivity of a trained network’s output to the inputs. The trained network for our method implies that the Lagrange multipliers used in the measuring of the saliency metric in the SVM are fixed values. The purpose of measuring the saliency metric, in other words, the calculation of sensitivity coefficients, is to rank the significance of feature inputs over the entire training set. It can also be easily noticed that the elements of the gradient vector defined in Eq. 15 can be considered as sensitivity coefficients. Therefore, we interchangeably use saliency analysis and sensitivity analysis in the implementation parts of the paper.

The sensitivity of the output to the inputs in the SVM is derived by solving the following partial derivative:

$$ \frac{{\partial y({\mathbf{x}}_{i} )}} {{\partial x_{{ik}} }} = \frac{{\partial {\left( {{\sum\limits_{s = 1}^{N_{{\text{s}}} } {\alpha _{s} d^{s} K({\mathbf{x}}_{i} ,{\mathbf{x}}_{s} ) + b} }} \right)}}} {{\partial x_{{ik}} }} = {\sum\limits_{s = 1}^{N_{{\text{s}}} } {\alpha _{s} d^{s} \frac{{\partial K({\mathbf{x}}_{i} ,{\mathbf{x}}_{s} )}} {{\partial x_{{ik}} }}} } $$

(17)

where N_s is the number of support vectors corresponding to non-zero Lagrange multipliers and k=1, 2,..., P.

Let us expand Eq. 17 for the Gaussian kernel function given in Eq. 18:

$$ K({\mathbf{x}}_{i} ,{\mathbf{x}}_{s} ) = {\text{e}}^{{\frac{{ - {\sum\limits_{l = 1}^P {(x_{{il}} - x_{{sl}} )^{2} } }}} {{\sigma ^{2} }}}} $$

(18)

Then take the derivative:

$$ \frac{{\partial K({\mathbf{x}}_{i} ,{\mathbf{x}}_{s} )}} {{\partial x_{{ik}} }} = - \frac{2} {{\sigma ^{2} }}(x_{{ik}} - x_{{sk}} ){\text{e}}^{{\frac{{ - {\sum\limits_{l = 1}^P {(x_{{il}} - x_{{sl}} )^{2} } }}} {{\sigma ^{2} }}}} $$

(19)

and:

$$ \frac{{\partial y({\mathbf{x}}_{i} )}} {{\partial x_{{ik}} }} = - \frac{2} {{\sigma ^{2} }}{\sum\limits_{s = 1}^{S_{N} } {\alpha _{s} d^{s} (x_{{ik}} - x_{{sk}} ){\text{e}}^{{\frac{{ - {\sum\limits_{l = 1}^P {(x_{{il}} - x_{{sl}} )^{2} } }}} {{\sigma ^{2} }}}} } } $$

(20)

The sensitivity can be calculated for any type of kernel function in accordance with Eq. 17, and the value depends upon the input feature x _ik and the support vectors x _s , as well as the converged Lagrange multipliers α _s . Then, the saliency metric of each feature is calculated for each k (k=1, 2,..., P) as follows:

$$ S_{{k,{\text{sal}}}} = \frac{{{\sum\limits_{i = 1}^N {{\left| {\frac{{\partial y({\mathbf{x}}_{i} )}} {{\partial x_{{ik}} }}} \right|}} }}} {N} $$

(21)

This measure allows a better estimation of the sensitivity over the entire input space [21]. Another useful measure of sensitivity used for the evaluation of input saliency was introduced in [22]. All these techniques can be used to obtain the relative significance of each input feature to the output.

The calculated saliency values are used to rank the relative significance of input features. On the other hand, the saliency metric does not give the number of feature elements which are to be discarded. So, a recursive algorithm is proposed here not only to discard redundant features, but also to find optimal solution as follows:

• Step 1 Initially, set k=p, where p is the length of the feature vector (x∈R^P)

• Step 2 If k>m, then:

  • Train and test the SVM using the feature set k

  • Calculate the saliency metric S _i , i=1, 2,...,  k by using Eqs. 17 and 21 for each feature candidate

  • Rank the saliency values S _i in a descending order as S₁>S₂>...>S _k

  • Delete m features with the smallest saliency values S_k+1−m,..., S _k (m could be 1 for a small k and could be more than 1 for a large k)

  • Train and test the SVM by using the remaining features corresponding to S₁,..., S_k−m values

  • Set k=k−m

• Step 3 Go to Step 2

After the iterative implementation is finished, the feature elements that produces the best performance in the SVM is obtained.

3 Application to real electroencephalographic data

3.1 Data acquisition and its properties

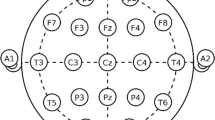
The EEG data used in this study were acquired from 18 subjects. Twelve of them are epileptic patients and six of them are normal. Eight epileptic patients’ and four normal subjects’ records are used in training, while the remaining six records are used in testing. The data were obtained from a clinical EEG monitoring system, which stores continuous EEG data on its hard disk. EEG data were acquired with Ag/AgCl disk electrodes placed using the 10–20 international electrode placement system. The recordings were obtained from 19 channels with a 256-Hz sampling frequency and were band-pass filtered between 1 Hz and 50 Hz. The data were then stored on both a hard disk and an optical disk.

First, all EEG records have been previously seen independently by two electroencephalographers (EEGers) and were labelled for SS candidates throughout the 19 channels. Then, the SS candidates for which there was no agreement between the two EEGers are treated as background EEG records. The total EEG length is about 144 h (average 8 h) and the ages of the subjects varied from 6 to 66 years (average 28 years).

Among the 18 EEG records, 12 of them are chosen for the training procedure. Each EEG record has an average length of 8 h. The subjects have an average age of 29 years in the training set. 2,148 SSs are determined by the EEGers for training procedure. The remaining six EEG records are used to test the performance of the trained system. Each test record has an average length of 8 h. 264 SSs are determined for the testing procedure. The subjects have an average age of 30 years in the testing procedure.

3.2 Normalisation process

Feature extraction processes are affected by the peak-to-peak amplitudes and the offset of the signals. In this study, prior to the feature extraction process, each EEG signal is normalised as follows:

• The peak-to-peak magnitudes of the EEG signal are normalised to 1 μV. Thus, it is assumed that the classification decision does not depend on the maximum amplitude of the EEG records.

• The mean value of the signal is fixed to zero by subtracting the mean of the signal from the original signal. Thus, the offset is removed from the signal.

The dependence of the feature extraction method to the peak-to-peak magnitude and offset of the signal is decreased by the normalisation procedure.

3.3 Feature extraction and selection

As described earlier, the duration of SSs lasts between 0.5 s to 3 s. This time interval is important and is our reference for the determination of the window size for pattern extraction. The patterns for the training and testing procedures are generated as follows. First, the EEG data is sampled at a rate of 256 Hz with a ~3-s (768-point) window. Then, the signal is scanned by the determined window by shifting throughout the signal. At all steps of the shifting procedures, each window’s 768 data points with their indices are stored as raw EEG patterns. By these processes, a training set is constructed with raw EEG patterns. As mentioned in Sect. 3.1, the extracted patterns are evaluated by two EEGers. From the results of the evaluation process, 2,148 SS patterns are chosen for training and 264 SS patterns are reserved for testing. The remaining patterns are evaluated as non-SS patterns. After the normalisation of these patterns, four different feature vectors from the same records are constructed and their performances are comparatively examined: (a) raw amplitude values, (b) discrete cosine transform (DCT) coefficients, (c) discrete wavelet transform (DWT) approximation coefficients and (d) adaptive autoregressive (AAR) coefficients.

First, the number of samples is reduced from 768 to 192 data points by using a down-sampling method with a 1:4 ratio. Then, the best features are selected by a modified adaptive feature selection method, which is described in detail with an algorithm in Sect. 2, for each feature set separately. At the beginning of the feature selection procedure, the SVM is trained using the feature set with the down-sampled 192 data points in accordance with the proposed recursive algorithm. After testing and calculating the performance of the system, saliency values are calculated by using Eqs. 20 and 21. After the saliency values are ranked in a descending order, m elements corresponding to the smallest saliency values are deleted. Here, m is a user-defined number in accordance with the length of the feature vector. Then, the SVM is retrained with the remaining features after deleting the redundant feature elements. This iterative implementation is repeated until the length of the feature vector is less than m (≤m). At each loop in the algorithm, the classification performance of the system is tested by using the testing data and is stored for determining the best features. So, the optimal input size is also determined, which is, indeed, the number of determined best feature elements giving the highest performance. If the dimension of the feature vector is large, the number of deleted elements corresponding to the smallest saliency values can be increased. Due to the nature of algorithm, the SVM is also trained and tested while the feature selection is implemented. All of these implementations are done for the four feature sets separately as follows:

The feature extraction of the first feature set involves the amplitude values of the data of length 192 data points. In this procedure, the number of samples is reduced to 32 as follows:

$$ y_{j} = \frac{1} {{24}}{\sum\limits_{i = 1}^{24} {x(i + 24(j - 1))} },\quad j = 1,2, \ldots ,32 $$

(22)

where x=[x(1), x(2),..., x(768)] is the original EEG signal of 768 samples, and y _j is the jth element of the new feature vector formed by taking the average of every 24 samples of the original EEG signal. The computing time is also decreased by reducing the number of samples for first feature set. From 32 average amplitude values, the best classification performance is obtained for a subset of 24 amplitude values. There is no significant increase in the performance of the system for more than 24 amplitude values (Fig. 3). The ordering of the elements for each feature vector in terms of significance level in a descending order is as follows:

k 1

k 2

k 3

k 4

k 5

k 6

k 7

k 8

k 9

k 10

k 11

k 12

k 13

k 14

k 15

k 16

k 17

k 18

k 19

k 20

k 21

k 22

k 23

k 24

c 3

c 1

c 4

c 28

c 15

c 22

c 6

c 7

c 21

c 24

c 9

c 17

c 18

c 29

c 31

c 32

c 2

c 8

c 5

c 20

c 16

c 19

c 23

c 24

k=[k₁, k₂,..., k₂₄] is the 24-dimensional new feature vector. c=[c₁, c₂,..., c₃₂] is a vector representing the averaged amplitude values of the signal.

Fig. 3

Block diagram of the adaptive linear estimator

The second feature set involves the DCT coefficients of the EEG data. From 192 DCT coefficients, the best classification performance is obtained for a subset of 16 DCT coefficients. The ordering of the elements (in a descending order) for each feature vector in terms of significance level is as follows for the DCT coefficients:

k 1

k 2

k 3

k 4

k 5

k 6

k 7

k 8

k 9

k 10

k 11

k 12

k 13

k 14

k 15

k 16

c 65

c 53

c 5

c 69

c 51

c 35

c 70

c 42

c 45

c 55

c 58

c 9

c 94

c 26

c 2

c 84

k=[k₁, k₂,..., k₁₆] is the 16-dimensional new feature vector. c=[c₁, c₂,..., c₁₉₂] is a vector that represents DCT coefficients of the down-sampled data (192 data points size).

The feature extraction of the third feature set involves the DWT approximation coefficients of the down-sampled EEG data. The feature vectors are formed using the Daubechies-2 wavelet [24]. For each feature vector, the wavelet approximation coefficients at the second, third and fourth levels (50+26+14=90) are calculated. Among the 90 DWT approximation coefficients, a subset of 18 coefficients gives the best performance of the system. Saliency analysis in this feature set showed the fourth-level DWT approximation coefficients to be more significant than the others:

k 1

k 2

k 3

k 4

k 5

k 6

k 7

k 8

k 9

k 10

k 11

k 12

k 13

k 14

k 15

k 16

k 17

k 18

a 14

a 54

a 84

a 124

a 144

a 44

a 34

a 64

a 74

a 114

a 104

a 24

a 94

a 134

a 53

a 213

a 123

a 242

$$ k = [k_1 ,k_2 ,\, \ldots ,\,k_{18} ]\;{\text{and}}\;a = [a_2^1 ,a_2^2 , \ldots ,a_2^{50} ,a_3^1 ,a_3^2 , \ldots ,a_3^{26} ,a_4^1 ,a_4^2 , \ldots ,a_4^{14} ] $$

where k represents the 18-dimensional new feature vector and a represents the DWT approximation coefficients at the second, third and fourth levels.

The fourth feature set is created by using the AAR estimation method [25]. Conventional autoregressive methods are appropriate if the signal does not change with time, but in real situations, the EEG signal is under the influence of several factors that are impossible to control. Therefore, block autoregressive methods may not track the slow change in the spectrum of non-stationary signal, as is the case of EEG signals. Here, this limitation of autoregressive methods is overcome by estimating the autoregressive parameters adaptively by using the least mean square method [26] for each sample (Fig. 3).

Here, AAR coefficients are calculated for each raw feature vector. The optimal order of AAR model is obtained as 15 by using the Akaike criterion [25]. Thus, the input dimension of each feature vector is reduced to 15. But, we couldn’t see a significant increase in the performance of the system for more than ten determined AAR coefficients. The ordering of the elements for each feature vector is as follows:

k 1	k 2	k 3	k 4	k 5	k 6	k 7	k 8	k 9	k 10
c 1	c 2	c 5	c 9	c 10	c 14	c 11	c 15	c 8	c 4

k=[k₁, k₂,...,  k₁₀] is the 10-dimensional new feature vector in a significance order. c=[c₁, c₂,...,  c₁₅] is a vector that represents the AAR coefficients. Here, the AAR coefficients can be evaluated as finite impulse response filter coefficients.

Consequently, the best features for four different feature sets are searched by using a sensitivity analysis based on the SVM. Thus, not only is the system optimised for having the best performance, but also, the input dimension is reduced. Therefore, the computing time is reduced and the network becomes smaller.

3.4 Implementation of the RB-SVM classifier

First, in order to visualise the problem, we restrict ourselves to the two features that contain some information about the class—namely, the duration and the average amplitude of the SSs. As can be seen from Fig. 4, the separation of a group of SSs from a group of non-SSs is not so trivial. In the RB-SVM classification, support vectors are represented, by circles as shown in Fig. 4. The value of C=100 gives the best result for this example.

Fig. 4

An example of SVM-based classification of the SSs into a two-dimensional case to visualise the classification problem for C=100: the solid line represents the decision boundary, the dashed line represents the maximised margins, the open squares represent SSs, the plus symbols represent non-SSs and the circles represent the support vectors

After the feature extraction, the feature sets are fed to the SVM for recognition of the SSs. SS patterns and non-SS patterns are represented by +1 and −1, respectively, in both the training and the testing procedures.

The first feature set, involving signal amplitudes, explained in Sect. 3.3, is fed to the RB-SVM classifier with C initially set to 100. The SVM is trained and tested until finding the best result in accordance with the algorithm presented in Sect. 2.3. The best result is obtained for a 24-data-points input size (Fig. 5). Thus, the input dimension is reduced to 24 by selecting the best feature elements. Then, the SVM classifier is performed for different C values with the determined 24 feature elements. The best result for Feature Set I is obtained for C=1,000 with 36 support vectors in the test. Testing the SVM in the recognition system shows an average sensitivity of 93.9%, an average specificity of 93.3% and an average accuracy of 93.6%.

Fig. 5

The effect of the input size, determined at each iteration of the adaptive feature selection algorithm, on the recognition accuracy for the first feature set involving averaged amplitude values (m=2)

For the second feature set, involving DCT coefficients, the same training and feature selection implementations are repeated without any changes. With the C value initially set to 100, the algorithm is applied to the set. The best result is obtained for a 16-data-points input size (Fig. 6). Then, the SVM classifier is again performed for different C values with the determined 16 feature elements. The best result for Feature Set II is obtained for C=100. The number of support vectors is 23 in this implementation. From the testing with Feature Set II, the performance of the system gives the best result among the four alternative feature sets with an average sensitivity of 97.7%, an average specificity of 97.4% and an average accuracy of 97.5%.

Fig. 6

The effect of the input size, determined at each iteration of the adaptive feature selection algorithm, on the recognition accuracy for the second feature set involving DCT coefficients (m=4)

For the third feature set, involving DWT approximation coefficients mentioned in Sect. 3.3, the same training and feature selection implementations are repeated. With the C value initially set to 100, the algorithm is again applied to the set. Then, the best result is obtained for a 18-data-points input size (Fig. 7). So, the input size is drastically reduced to 18 by selecting the best feature elements. Then, the SVM classifier is again performed for different C values with the determined 18 features. The best result for Feature Set III is obtained for C=100, which is the same as in the second feature set. The number of support vectors is 26, which also corresponds to the number of hidden neurons in the RB-SVM classifier. After the testing procedure, the performance of the system results in an average sensitivity of 95.1%, an average specificity of 94.4% and an average accuracy of 94.7%.

Fig. 7

The effect of the input size, determined at each iteration of the adaptive feature selection algorithm, on the recognition accuracy for the third feature set involving DWT approximation coefficients (m=4)

Finally, for the last feature set involving AAR coefficients, the same implementations are repeated. The best result is obtained for a ten-data-points input size (Fig. 8). The best result for Feature Set IV is also obtained for C=100. The number of support vectors is 22. At the end of the testing procedure, the performance of the system results in an average sensitivity of 95.4%, an average specificity of 95.4% and an average accuracy of 95.4%.

Fig. 8

The effect of the input size, determined at each iteration of the adaptive feature selection algorithm, on the recognition accuracy for the fourth feature set involving AAR coefficients (m=1)

4 Results and discussion

The system is evaluated by using 19 channel clinical sleep EEG records of 18 subjects; six records are used for testing purposes and the rest are used for training. The proposed system has been developed using MATLAB 6.0. The tests are performed on a Pentium Celeron 400 MHz PC computer. The recognition procedure is performed off-line on data stored on the computer’s hard disk.

The performance of the automated recognition system is determined by measuring the sensitivity, specificity and accuracy [27]. The sensitivity is the ratio of true positives to the total number of SSs determined by the experts. Events are called “true positive” when both our system and the experts detect them as SSs. The specificity is the ratio of “true negative (correct rejection)” to the sum of the number of “true negatives” with “false positives.” The accuracy is the ratio of the total number of true positives and true negatives to the total number of true positives, false positives, true negatives and false negatives.

Table 1 gives the performance of the system in terms of sensitivity, specificity and accuracy for four different feature sets. It can be seen that the performance of the system results in 93.9% average sensitivity, 93.3% average specificity and 93.6% average accuracy for Feature Set I. The best results obtained for the second feature set involving DCT coefficients are 97.7% average sensitivity, 97.4% average specificity, and 97.5% average accuracy. The performance of the system for Feature Set III, involving DWT approximation coefficients, results in an average sensitivity of 95.1%, an average specificity of 94.4% and an average accuracy of 94.7%. And lastly, the performance of the system results in 95.4% average sensitivity, 95.4% average specificity and 95.4% average accuracy for Feature Set IV involving AAR coefficients.

Table 1 The performance of the system for test set in terms of sensitivity, specificity and accuracy

The recognition process is performed in three stages, comprising of normalisation process, feature extraction and an SVM network as the classifier. Each stage is carefully chosen to enhance the performance of the system.

The feature selection method is started with the perturbation method and is adapted to the SVM by using saliency (sensitivity) analysis. This modified feature selection algorithm not only increases the performance of the system, but it also highly decreases the computation time. The proposed feature selection method can also be used for all kinds of classification problems, especially for high input dimensional spontaneous signals.

In the classification task, we used a RB-SVM due to its power in binary classification problems. It can be observed that the SVM has a good generalisation ability. The number of neurons in the hidden layer, which is equal the number of support vectors, is determined automatically. On the other hand, a similar type of neural network, such as backpropagation multilayer perceptrons (MLPs), has some disadvantages in determining the number of neurons in a hidden layer and suffer from local minima problem. For determining the number of hidden layer nodes using backpropagation MLPs, a lot of trials need to be done. Similarly, a radial basis function network (RBFN) also needs to be trained several times to determine the number of centres. The determination of centres is also another disadvantage according to SVMs. Although there exist some supervised techniques for determining the centres of an RBFN, it suffers from a local minima problem. We examined and observed all of these advantages of SVMs and disadvantages of other types of neural networks in our previous study concerning the detection of spikes in EEG data [28].

Maintaining high flexibility of the system is also an important point. Waveforms differ greatly between different subjects, so the system must be flexible in order to retain efficiency under various circumstances. In the present system, we use an adaptive feature selection method directly related to the SVM. The system adjusts its parameters dynamically when the characteristics of the input data change. Thus, it is more robust for data from different subjects and also for different kinds of signals.

A comparison of our system with other systems given in the literature is very difficult due to the wide range of different types of measurement signal and classification techniques. Therefore, we could not give a comparison in terms of performance, but it can be seen that our proposed novel system performed in a very well in terms of sensitivity, specificity and accuracy levels, which were 97.7%, 97.4% and 97.5% respectively. So, the high performance of our system is comparable to the results reported in the literature, and also, the performance of the proposed system can be regarded to be as good as the experts’ opinions.

In conclusion, this study introduces a novel recognition system based on SVMs for the purpose of SSs detection that will contribute to the clinical applications as a modular system. The proposed system accomplishes normalisation, adaptive feature extraction and classification tasks for the recognition of SSs. In the feature extraction task, the best features for four different feature sets are determined by using a modified sensitivity analysis based on SVMs. Thus, not only is the system optimised for having the best performance, but also, the input dimension is reduced, meaning that the computing time is reduced and the network becomes smaller. Consequently, the comparison of our system to the results obtained by experts was favourable in providing the right decision and reducing the detection time.