Optimized growth and reorientation of anisotropic material based on evolution equations

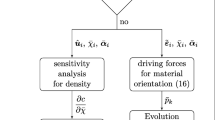
Abstract

Modern high-performance materials have inherent anisotropic elastic properties. The local material orientation can thus be considered to be an additional design variable for the topology optimization of structures containing such materials. In our previous work, we introduced a variational growth approach to topology optimization for isotropic, linear-elastic materials. We solved the optimization problem purely by application of Hamilton’s principle. In this way, we were able to determine an evolution equation for the spatial distribution of density mass, which can be evaluated in an iterative process within a solitary finite element environment. We now add the local material orientation described by a set of three Euler angles as additional design variables into the three-dimensional model. This leads to three additional evolution equations that can be separately evaluated for each (material) point. Thus, no additional field unknown within the finite element approach is needed, and the evolution of the spatial distribution of density mass and the evolution of the Euler angles can be evaluated simultaneously.

Appendices

A Lagrange shift approach

In [32], we introduced the Lagrange shift approach as an easy-to-handle and numerical stable approach to nature-like growth. We define the growth function $\varrho (t)$ in Eq. (17) for the constraint controlled by the Lagrange multiplier by aid of one numerical parameter $0 < \lambda _\mathrm {S} \le 1$ as

$$\begin{aligned} \varrho (t) := \left( 1-\lambda _\mathrm {S}\right) \rho _0(t) = \left. \frac{1-\lambda _\mathrm {S}}{V_\Omega } \displaystyle \int _\Omega {\frac{1}{f\left( \chi (t)\right) }} \, \;\!\mathrm {d}V\right| _{\lambda = 0}\nonumber \\ \end{aligned}$$

(67)

with $\rho _0(t)$ being the unrestrictedly grown structure volume for the time step t. The prefactor $1-\lambda _\mathrm {S}$ scales the behavior from unrestricted growth ($\lambda _\mathrm {S}=0$) to constant structure volume ($\lambda _\mathrm {S}=1$). Since the trivial solution, in which structure volume is generated everywhere within the design space, is undesired, the unrestricted growth is disabled by only allowing values $\lambda _\mathrm {S}>0$.

For the derivation of the Lagrange multiplier given in Eq. (44), we take the time derivative for the constraint in Eq. (17) which is supposed to be controlled by the Lagrange multiplier. This yields

$$\begin{aligned} \dot{g}(\chi ) = - \displaystyle \int _\Omega {\frac{1}{V_\Omega }\frac{f'(\chi )}{f(\chi )^2} \dot{\chi }} \, \;\!\mathrm {d}V - \dot{\varrho }(t) \mathop {=}\limits ^{!}0 \end{aligned}$$

(68)

Inserting the time derivative of Eq. (67)

$$\begin{aligned} \dot{\varrho }(t) = \left. \frac{(1-\lambda _\mathrm {S})}{V_\Omega } \displaystyle \int _\Omega {-\frac{f'(\chi )}{f(\chi )^2} \dot{\chi }} \, \;\!\mathrm {d}V\right| _{\lambda = 0} \end{aligned}$$

(69)

and the evolution equation for $\dot{\chi }$ according to Eq. (42) results in

$$\begin{aligned} \lambda = \lambda _\mathrm {S} \ V_\Omega \ \frac{\displaystyle \displaystyle \int _\Omega {\left( - p_\chi + \frac{\overline{\Delta \chi }_\mathrm {GP}}{V_\mathrm {e}} + \gamma \right) \frac{f'(\chi )}{f(\chi )^2}} \, \;\!\mathrm {d}V}{\displaystyle \displaystyle \int _\Omega {\left( \frac{f'(\chi )}{f(\chi )^2}\right) ^2} \, \;\!\mathrm {d}V} \end{aligned}$$

(70)

For more details see the original publication [32].

If the optimization for a prescribed (constant) structure volume is desired, it is possible to simply set $\lambda _\mathrm {S} = 1$. For numerical reasons, this is inappropriate, because only the growth rate is controlled by $\dot{\varrho }(t) = 0$, which can result in cumulative rounding errors within simulation time. Thus, we define

$$\begin{aligned} \dot{\varrho }^{(i+1)} = \frac{1}{\Delta t} \left( \varrho _\mathrm {target} - \displaystyle \frac{1}{V_\Omega }\displaystyle \int _\Omega {\frac{1}{f(\chi ^{(i)})}} \, \;\!\mathrm {d}V \right) \end{aligned}$$

(71)

for the growth function to grant (constant) relative structure volumes $\varrho _\mathrm {target}$, by defining the growth for the next iteration step $\Delta t \, \dot{\varrho }^{(i+1)}$ as the difference between the target structure volume $\varrho _\mathrm {target}$ and the current structure volume given by $\displaystyle \frac{1}{V_\Omega }\displaystyle \int _\Omega {\frac{1}{f(\chi ^{(i)})}} \, \;\!\mathrm {d}V$.

B Adaptive viscosity

The following relations have already been presented in [32] and are repeated here for convenience. More details are given in the original publication. The dissipation parameter $r_{\chi }$ fulfills the purpose of the viscosity in our rate-dependent approach and thus controls the velocity of the local growth. The maximal local growth rate in nature is a given value. However, we are not interested (at the moment) in modeling natural growth with accurate behavior in time. Instead, we use the viscosity to provide the interval constraint $\chi \in \, [0,1]$ and to replace the Kuhn–Tucker parameter $\gamma$.

For each internal variable $\chi$, a viscosity $\tilde{r}_\chi ^{(i)}$ will be calculated for which the specific $\chi$ would reach the interval border $\chi \in \, \{0,1\}$ at the iteration step (i). Let us introduce some abbreviations

$$\begin{aligned} F^{(i-1)}&:= p_\chi ^{(i-1)} - \frac{\overline{\Delta \chi }_\mathrm {GP}^{(i-1)}}{V_\mathrm {e}} \end{aligned}$$

(72)

$$\begin{aligned} \lambda _\mathrm {n}^{(i-1)}&:= \displaystyle \int _\Omega {-F^{(i-1)}\frac{f'\left( \chi ^{(i-1)}\right) }{f\left( \chi ^{(i-1)}\right) ^2}} \, \;\!\mathrm {d}V \end{aligned}$$

(73)

$$\begin{aligned} \lambda _\mathrm {d}^{(i-1)}&:= \displaystyle \displaystyle \int _\Omega {\left( \frac{f'\left( \chi ^{(i-1)}\right) }{f\left( \chi ^{(i-1)}\right) ^2}\right) ^2} \, \;\!\mathrm {d}V \end{aligned}$$

(74)

$$\begin{aligned} \lambda&= V_\Omega \frac{\lambda _\mathrm {n} - \tilde{r}_\chi ^{(i)} \ V_\Omega \ \dot{\varrho }\left( t^{(i)}\right) }{\lambda _\mathrm {d}} \end{aligned}$$

(75)

The evolution equation for the compliance parameter can then be written as

$$\begin{aligned} \dot{\chi }^{(i)}= & {} \frac{1}{\tilde{r}_\chi ^{(i)}}\left[ \frac{\lambda _\mathrm {n}^{(i-1)} - \tilde{r}_\chi ^{(i)} \ V_\Omega \ \dot{\varrho }\left( t^{(i)}\right) }{\lambda _\mathrm {d}^{(i-1)}}\right. \nonumber \\&\left. \left( \frac{f'\left( \chi ^{(i-1)}\right) }{f\left( \chi ^{(i-1)}\right) ^2}\right) ^2 + F^{(i-1)}\right] \end{aligned}$$

(76)

We define the individual rate of internal variable so that in each case the interval border for the internal variable is reached

$$\begin{aligned} \dot{\chi }^{(i)} = \dot{\tilde{\chi }}^{(i)} = {\left\{ \begin{array}{ll} \frac{1-\chi ^{(i-1)}}{\Delta t} , \quad \dot{\chi }^{(i-1)} > 0 \\ \frac{-\chi ^{(i-1)}}{\Delta t} , \quad \dot{\chi }^{(i-1)} \le 0 \end{array}\right. } \end{aligned}$$

(77)

This leads to

$$\begin{aligned} \tilde{r}_\chi ^{(i)} = \frac{ F^{(i-1)}\ \lambda _\mathrm {d}^{(i-1)} \ f\left( \chi ^{(i-1)}\right) ^2 + \lambda _\mathrm {n}^{(i-1)}\ f'\left( \chi ^{(i-1)}\right) }{\dot{\tilde{\chi }}^{(i)} \ \lambda _\mathrm {d}^{(i-1)} \ f\left( \chi ^{(i-1)}\right) ^2 + V_\Omega \ \dot{\varrho }\left( t^{(i)}\right) \ f'\left( \chi ^{(i-1)}\right) }\nonumber \\ \end{aligned}$$

(78)

Equation (78) needs to be evaluated for each (discretized) internal variable $\chi$. If the global viscosity becomes the maximum of all $\tilde{r}_\chi {(i)}$, the internal variable(s) corresponding to the maximal $\tilde{r}_\chi {(i)}$ will reach the interval border $\chi \in \, \{0,1\}$, whereas all other internal variables are too “slow” to reach any interval border. Due to the explicit assumption in the evolution equations, interval transgression is still possible and numerical instabilities can occur by simply defining the maximal $\tilde{r}_\chi {(i)}$ as the global viscosity for the compliance parameter. Therefore, we introduce the safety factor $r_\mathrm {S} > 1$ that is a plain multiplier to the adaptive viscosity to slow down growth and to prevent interval transgression. The global viscosity $r_{\chi }{(i)}$ for the current iteration step is then

$$\begin{aligned} r_{\chi }^{(i)} = r_\mathrm {S} \ \max \left\{ \tilde{r}_\chi ^{(i)} \right\} \end{aligned}$$

(79)