Magnetic effect on the creeping flow around a slightly deformed semipermeable sphere

Abstract

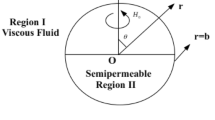
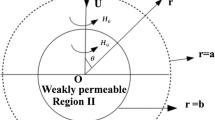
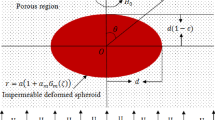
This paper presents steady axisymmetric creeping motion of a conducting, incompressible viscous fluid past a weakly permeable slightly deformed sphere in the presence of transverse magnetic field. The Stokes approximation of momentum equation and Darcy’s law together with Lorentz force are used for the flow outside and within the semi-permeable particle. The governing equations are changed into dimensionless form, and resulting equations are solved using separation of variables method. We have determined the resistance force exerted on the oblate spheroid in the presence of magnetic field as a particular case of an approximate sphere. The impact of Hartmann numbers, permeability and deformation parameter on the coefficient of drag and the streamline pattern is exhibited graphically. Some special cases are deduced from the current study and compared with some previous results. The outcome clarifies that the Hartmann numbers enhance the drag on the oblate spheroid in comparison with prolate spheroid.

Appendix

We get the following equations by using the boundary conditions (Eq. 15)–(Eq. 17) to the 1st order in ${\beta }_{m}$:

$$\left[ {1 + a_{2} + b_{2} K_{{\frac{3}{2}}} \left( \alpha \right) - c_{2} } \right]P_{1} \left( \zeta \right) + \left[ {2 - a_{2} - b_{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right) - 2c_{2} } \right]P_{1} \left( \zeta \right)G_{m} \left( \zeta \right)\beta _{m} + \sum\limits_{{n = 3}}^{\infty } {\left[ {A_{n} + B_{n} K_{{n - \frac{1}{2}}} \left( \alpha \right) - C_{n} } \right]} P_{{n - 1}} (\zeta ) = 0,$$

(39)

$$\left[ {2 - a_{2} - b_{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right)} \right]G_{2} \left( \zeta \right) + \left[ {2 + 2a_{2} + b_{2} (\alpha ^{2} + 2)K_{{\frac{3}{2}}} \left( \alpha \right)} \right]G_{2} \left( \zeta \right)G_{m} \left( \zeta \right)\beta _{m} + \sum\limits_{{n = 3}}^{\infty } {\left[ {\left( {1 - n} \right)A_{n} - B_{n} \left( {\left( {n - 1} \right)K_{{n - \frac{1}{2}}} \left( \alpha \right) + \alpha K_{{n + \frac{1}{2}}} \left( \alpha \right)} \right)} \right]} G_{n} (\zeta ) = 0,$$

(40)

$$\left[{\alpha }^{2}-\frac{{\alpha }^{2}}{2}{a}_{2}-{\beta }^{2}{c}_{2}\right]{P}_{1}\left(\zeta \right)+\left[{\alpha }^{2}+{\alpha }^{2}{a}_{2}-{\beta }^{2}{c}_{2}\right]\beta {}_{m}{G}_{m}\left(\zeta \right){P}_{1}\left(\zeta \right)-\sum_{n=3}^{\infty }\left[\frac{{\alpha }^{2}}{n}{A}_{n}+\frac{{\beta }^{2}}{n-1}{C}_{n}\right]{P}_{n-1}(\zeta )=0.$$

(41)

Equating the leading terms of Eqs. (39) to (41) to zero, we obtain.

$$1 + a_{2} + b_{2} K_{{\frac{3}{2}}} \left( \alpha \right) - c_{2} = 0,$$

(42)

$$2 - a_{2} - b_{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right) = 0,$$

(43)

$${\alpha }^{2}-\frac{{\alpha }^{2}}{2}{a}_{2}-{\beta }^{2}{c}_{2}=0.$$

(44)

Solving Eqs. (42)–(44), we find that

$$\left. {\begin{array}{*{20}c} {a_{2} = \frac{{2\left[ {\alpha ^{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right) - \beta ^{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + 3K_{{\frac{3}{2}}} \left( \alpha \right)} \right)} \right]}}{{\alpha \left( {\alpha ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + 2\beta ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + \alpha K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}},} \\ {b_{2} = \frac{{6\beta ^{2} }}{{\alpha \left( {\alpha ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + 2\beta ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + \alpha K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}},} \\ {c_{2} = \frac{{3\alpha \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}}{{\left( {\alpha ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + 2\beta ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + \alpha K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}}.} \\ \end{array} } \right\}$$

(45)

Substituting these above values into (39)–(41), we obtain

$$\left[ { - \frac{{6\alpha \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}}{{\alpha \left( {\alpha ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + 2\beta ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + \alpha K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}}} \right]\beta _{m} G_{m} \left( \zeta \right)P_{1} \left( \zeta \right) + \sum\limits_{{n = 3}}^{\infty } {\left[ {A_{n} + B_{n} K_{{n - \frac{1}{2}}} \left( \alpha \right) - C_{n} } \right]} P_{{n - 1}} (\zeta ) = 0,$$

(46)

$$\left[ {\frac{{6\alpha ^{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right) + \beta ^{2} K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}}{{\alpha \left( {\alpha ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + 2\beta ^{2} K_{{\frac{1}{2}}} \left( \alpha \right) + \alpha K_{{\frac{3}{2}}} \left( \alpha \right)} \right)}}} \right]\beta _{m} G_{m} \left( \zeta \right)G_{2} \left( \zeta \right) + \sum\limits_{{n = 3}}^{\infty } {\left[ {\left( {1 - n} \right)A_{n} + B_{n} (nK_{{n - \frac{1}{2}}} \left( \alpha \right) - \alpha K_{{n + \frac{1}{2}}} \left( \alpha \right))} \right]} G_{n} (\zeta ) = 0,$$

(47)

$$\left[ {3\alpha ^{2} \left( {\alpha ^{2} - \beta ^{2} } \right)K_{{\frac{1}{2}}} \left( \alpha \right) + 3\alpha \left( {\alpha ^{2} - 3\beta ^{2} } \right)K_{{\frac{3}{2}}} \left( \alpha \right)} \right]\beta _{m} G_{m} \left( \zeta \right)P_{1} \left( \zeta \right) - \sum\limits_{{n = 3}}^{\infty } {\left[ {\frac{{\alpha ^{2} }}{n}A_{n} + \frac{{\beta ^{2} }}{{n - 1}}C_{n} } \right]} P_{{n - 1}} (\zeta ) = 0.$$

(48)

To solve above three equations for remaining arbitrary constants ${A}_{n}, {B}_{n} \mathrm{and} {C}_{n},$ we require the identity.

$${G}_{m}\left(\zeta \right){G}_{2}\left(\zeta \right)=\frac{-\left(m-2\right)(m-3)}{2\left(2m-1\right)(2m-3)}{G}_{m-2}\left(\zeta \right)+\frac{m(m-1)}{\left(2m+1\right)(2m-3)}{G}_{m}\left(\zeta \right)-\frac{(m+1)(m+2)}{2\left(2m-1\right)(2m+1)}{G}_{m+2}\left(\zeta \right),$$

(49)

and

$${G}_{m}\left(\zeta \right){P}_{1}\left(\zeta \right)=\frac{\left(m-2\right)}{\left(2m-1\right)(2m-3)}{P}_{m-3}\left(\zeta \right)+\frac{1}{\left(2m+1\right)(2m-3)}{P}_{m-1}\left(\zeta \right)-\frac{(m+1)}{\left(2m-1\right)(2m+1)}{P}_{m+1}\left(\zeta \right),$$

(50)

valid for $m>2$. Using these above identities in equations (46) to (48) when $n\ne m-2$, $m$, $m+2$, we see that the coefficient identically becomes to zero, that is

$${A}_{n}={B}_{n}={C}_{n}=0.$$

(51)

On the other hand, the system of equations in terms of ${A}_{n}, {B}_{n} \mathrm{and} {C}_{n},$ when $n$ is equal to $m-2$, $m$, and $m+2$, we get the following expressions:

$${\Delta }_{1}{\Phi }_{n}+{A}_{n}+{B}_{n}{K}_{n-\frac{1}{2}}\left(\alpha \right)-{C}_{n}=0,$$

(52)

$${\Delta }_{2}{\lambda }_{n}+{\left(1-n\right)A}_{n}+{B}_{n}\left(n{K}_{n-\frac{1}{2}}\left(\alpha \right){-\alpha K}_{n+\frac{1}{2}}\left(\alpha \right)\right)=0,$$

(53)

$${\Delta }_{3}{\Phi }_{n}-\frac{{\alpha }^{2}}{n}{A}_{n}-\frac{{\beta }^{2}}{n-1}{C}_{n}=0,$$

(54)

where

$$\left. {\begin{array}{*{20}c} {\Delta _{1} = 2 - a_{2} - b_{2} \left( {\alpha K_{{\frac{1}{2}}} \left( \alpha \right) + K_{{\frac{3}{2}}} \left( \alpha \right)} \right) - 2c_{2} ,} \\ {\Delta _{2} = 2 + 2a_{2} + b_{2} \left( {\alpha ^{2} + 2} \right)K_{{\frac{3}{2}}} \left( \alpha \right),} \\ {\Delta _{3} = \alpha ^{2} + \alpha ^{2} a_{2} + \beta ^{2} c_{2} ,} \\ {\Phi _{n} = \frac{{\beta _{n} }}{{\left( {2n + 1} \right)\left( {2n - 3} \right)}},} \\ {\lambda _{n} = \frac{{n\left( {n - 1} \right)\beta _{n} }}{{\left( {2n + 1} \right)\left( {2n - 3} \right)}}.} \\ \end{array} } \right\}$$

Solving Eqs. (52) to (54), we get the expression for ${A}_{n} {B}_{n}$ and ${C}_{n}$, when $n= m-2$, $m$, $m+2$.