Bayesian inference of constitutive parameters from video data of the impact dynamics of a ball

Abstract

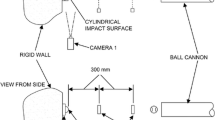
The trajectory of a ball impacting with an angle on a rigid boundary is recorded with a high-speed camera and the dynamics is reconstructed in a computer. Several experiments are carried out in order to obtain statistical distributions of the trajectory. On the other hand, a continuum model of a viscoelastic material ball simulates the experiment. If the values of the constitutive parameters (e.g. elastic and viscous modulus, friction coefficient, etc.) in the numerical model are correct, the simulated dynamics and the experimental data should match. In this study, the Bayesian inference is applied to identify two constitutive parameters (the friction and viscous coefficients) through statistical measures. The methodology shows to provide a useful tool to solve an inverse problem with a stochastic approach which allows to reference the results in a statistic frame starting from indirect and sparse information.

Appendices

Appendix A Weak formulation

In order to solve the equations of motion, they are rewritten in their weak form. Let $\mathbf {W}$ be a test vector field (the admissible functions) of variables referred to the body in its material configuration. Multiplying the equations of motion by $\mathbf {W}$ and integrating over all domain $V_{0}$:

$$\begin{aligned}&\int _{V_{0}}\left( \nabla _{X}\cdot \mathbf {T_{R}}+\rho _{0}\mathbf {b}- \rho _{0}\ddot{\mathbf {x}}\right) \cdot \mathbf {W}\,\,\hbox {d}V_{0}=0 \end{aligned}$$

(15)

$$\begin{aligned}&\int _{\varGamma }\left( \mathbf {t_{R}}\cdot \mathbf {W}\right) \hbox {d}A_{0}\nonumber \\&\quad +\,{{{\int _{V_{0}}{\left[ \rho _{0}\left( \mathbf {b}-\ddot{\mathbf {x}}\right) \cdot \mathbf {W}-\mathbf {T_{R}}\cdot \nabla \mathbf {W}\right] \hbox {d}V_{0}=0}}}} {{}} \end{aligned}$$

(16)

where Eq. 16 is obtained after integrating Eq. 15 by parts (using Green’s formula). The surface integral is divided into two parts, $\varGamma ^{1}$ and $\varGamma ^{2}$. Suppose that the position vector $\mathbf {x}$ is prescribed in a part of the boundary’s surface $\varGamma ^{1}$, where the geometrical boundary conditions are imposed $\varGamma ^{1}=\varGamma _{D}$, and the traction is given at the other part ($\varGamma ^{2}=\varGamma _{F}+\varGamma _{C}$.) With this scheme, the Robin boundary condition corresponds to a natural one. Then:

$$\begin{aligned} \mathbf {x}=\bar{\mathbf{x}}\,\,\,\hbox {on}\,\,\varGamma ^{1}\,\,\,\mathrm {and}\,\,\, {\mathbf{t}_{\mathbf{R}}=\bar{\mathbf{t}}_{\mathbf{R}}}\,\,\,\hbox {on}\,\,\varGamma ^{2}. \end{aligned}$$

(17)

In the case of non-homogeneous essential (geometrical) boundary conditions, the solution $\mathbf {x}(\mathbf {X},t)$ must satisfy Eq. 17 on $\varGamma ^{1}$ but the test function $\mathbf {W}$ must satisfy the homogeneous essential boundary condition. Then, in the variational problem Eq. 16, the admissible test functions $\mathbf {W}$ are defined as

$$\begin{aligned}&\mathbf {W(X)} \in \hbox {Adm}_{1}\nonumber \\&\quad = {{{\left\{ \mathbf {W}\mid \mathbf {W}=0\,\,\hbox {on}\,\,\varGamma ^{1}\,\,\hbox {and}\,\,\int \left( {\nabla W}\right) ^{2}\hbox {d}V_{0}<\infty \right\} }}} \end{aligned}$$

(18)

and the solution $\mathbf {x(X)}$

$$\begin{aligned}&\mathbf {x(X,}t) \in \hbox {Adm}_{2}\nonumber \\&\quad = {{\left\{ \mathbf {x}\mid \mathbf {x}=\bar{\mathbf {x}}\,\,\hbox {on}\,\,\varGamma ^{1}\,\,\hbox {and}\,\,\int \left( \mathbf {T_{R}}\right) ^{2}\hbox {d}V_{0}<\infty \right\} }} \end{aligned}$$

(19)

with this, the natural boundary conditions in Eq. 16 are automatically imposed. Then, the surface integral in Eq. 16 reduces to

$$\begin{aligned} \int _{\varGamma }\left( \mathbf {t_{R}}\cdot \mathbf {W}\right) \hbox {d}A_{0}= \int _{\varGamma ^{2}}\left( \bar{\mathbf {t}_{R}}\cdot \mathbf {W}\right) \hbox {d}A_{0} \end{aligned}$$

(20)

where $\bar{\mathbf {t}_{R}}$ is the value (data) of the traction $\mathbf {t_{R}}$ in the boundary. In the case of a bouncing ball, the traction vectors are null on the external body surface $\varGamma _{F}$ with exception of the contact surface $\varGamma _{C}$. On the other hand, the part $\varGamma _{D}$ is not presented in this scheme because it corresponds to the prescribed motion $\varGamma ^{1}$, not imposed in this problem.

Finally, the variational problem consists in finding the vector $\mathbf {x(X,}t)$, implicit in $\mathbf {T}_{\mathbf {R}}$ via constitutive equation, such that

$$\begin{aligned} {\left\{ \begin{array}{ll} \forall \mathbf {W}\in \hbox {Adm}_{1}\, \text{ find } \,\mathbf {x}\in \hbox {Adm}_{2}, \text{ that } \text{ satisfies }\\ \int _{\varGamma ^{2}}\left( {\bar{\mathbf{t}}_{\mathbf{R}}}\cdot \mathbf {W} \right) dA_{0}=-\int _{V_{0}}\left[ \rho _{0}\left( \mathbf {b}-\ddot{\mathbf {x}}\right) \cdot \mathbf {W}-\mathbf {T_{R}}\cdot \nabla \mathbf {W}\right] \hbox {d}V_{0} \end{array}\right. } \end{aligned}$$

(21)

and the initial conditions,

$$\begin{aligned} \mathbf {x}(\mathbf {X},t_{0})=\mathbf {x_{0}}(\mathbf {X});\,\,\,{\dot{\mathbf {x}}} (\mathbf {X},t_{0})=\mathbf {v}(\mathbf {X}) \end{aligned}$$

(22)

where $\mathbf {v(X)}$ is the known initial velocity field. These initial conditions are taken through the experimental data i.e. the average values of incidence angle ($\theta _{i}$), spin and speed ($v_{i}$), taken from the 55 samples of the impact test.

Appendix B Galerkin method and discretization in finite elements

Let $\left\{ \mathbf {\phi _{j}}\right\} \in Adm_{1}$ be a basis of a subspace of a Hilbert space. In this paper $\mathbf {\phi }_{\mathbf {i}}$ are shape vector functions and each component is a 3-dimensional quadratic polynomial. Let the function $\mathbf {x}(\mathbf {X},t)$ be expanded in a series of the this vectorial functions $\mathbf {\phi _{i}(X)}$

$$\begin{aligned} \mathbf {x}(\mathbf {X},t)\simeq \sum _{i=1}^{n}\mathbf {\phi _{i}(X)}c_{i}(t). \end{aligned}$$

(23)

Here $c_{i}(t)$ are functions only of time.

Replacing Eq. 23 in Eq. 1 and integrating on the whole domain:

$$\begin{aligned} \int \left[ \nabla _{X}\cdot \mathbf {T_{R}\left( x\right) }+\rho _{0} \left( \mathbf {b}-\sum _{i=1}^{n}\mathbf {\phi _{i}(X)}c_{i}(t)\right) \right] {\phi _{\mathbf{j}}(\mathbf{X})}\,\hbox {d}V_{0}=0 \end{aligned}$$

(24)

for j from 1 to n. $\mathbf {T_{R}(x)}$ means that the first Piola stress tensor is calculated from $\mathbf {x}(\mathbf {X},t)$ through constitutive relations Eq. 4 and definition of the second Piola stress. At last, using Eq. 16 we get:

$$\begin{aligned}&\int _{\varGamma _{j}^{2}}\left( \mathbf {t_{R}(x)}\cdot \phi _{j}\right) \hbox {d}A_{0}\nonumber \\&\quad +{{{\int _{V_{j}}}{\left[ \rho _{0}\left( \mathbf {b}-\sum _{i=1}^{n} {\phi _{\mathbf{i}}}\ddot{c}_{i}(t)\right) \cdot {\phi _{\mathbf{j}}}-\mathbf {T_{R}} \cdot \nabla {\phi _{\mathbf{j}}}\right] \hbox {d}V_{j}}}} =0 \end{aligned}$$

(25)

where $V_{j}$ is the volume of the jth element.

This numerical calculation is made in the environment of the FlexPDE version 7 software [21].