A high-precision progressive damage model based on generalized mixed finite element method

Abstract

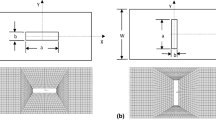
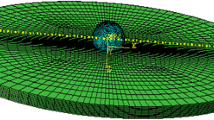
A novel three-dimensional progressive damage model based on generalized mixed finite element method (GMPDM) was established to investigate the strength and failure behavior of notched composite laminate plate. Firstly, the stress distribution of notched isotropic plate under tension is studied, and the results are compared with the analytical solution to verify the high accuracy of the generalized mixed finite element method. Then, the strength and failure modes of three notched composite laminates are studied. The results are compared with the several groups of results to verify the high-precision of the developed GMPDM method, respectively.

Appendix 1

In the process of solving material nonlinearity, the total stress $\sigma ^{n}$ should be expressed in terms of the sum of the previous stresses $\sigma ^{n-1}$ and the incremental stresses $\Delta \sigma$.

$$\begin{aligned} \sigma ^{n}=\sigma ^{n-1}+\Delta \sigma \end{aligned}$$

(16)

Equivalent expression of Eq. (4) without considering the body force is as follows:

$$\begin{aligned} \Pi _G^n = \int _V { - \frac{1}{4}{\sigma ^T}{S^{n - 1}}\sigma + \frac{1}{2}{\sigma ^T}\varepsilon + \frac{1}{4}{\varepsilon ^T}{C^{n - 1}}\varepsilon \hbox {d}V} - \int _S {{{\bar{T}}^T}u\hbox {d}S} \end{aligned}$$

(17)

Substituting Eq. (16) into Eq. (17), we can obtain

$$\begin{aligned} \mathrm{{\Pi }}_G^n= & {} \int _V { - \frac{1}{4}{{\left( {{\sigma ^{n - 1}} + \Delta \sigma } \right) }^T}{S^{n - 1}}\left( {{\sigma ^{n - 1}} + \Delta \sigma } \right) } \nonumber \\&+ \frac{1}{2}{\left( {{\sigma ^{n - 1}} + \Delta \sigma } \right) ^T}\varepsilon + \frac{1}{4}{\varepsilon ^T}{C^{n - 1}}\varepsilon \hbox {d}V\nonumber \\&- \int _S {{{\bar{T}}^T}\Delta u\hbox {d}S} \end{aligned}$$

(18)

The simplified Eq. (18) is as follows:

$$\begin{aligned} \prod \nolimits _{G}^n= & {} \int _V {\Delta {\sigma ^T}{S^{n - 1}}\Delta \sigma + 2{{\left( {\Delta \sigma } \right) }^T}\varepsilon - {\varepsilon ^T}{C^{n - 1}}\varepsilon \hbox {d}V} + 4\int _S {{{\bar{T}}^T}\Delta u\hbox {d}S} \nonumber \\&+ \,\int _V {{{\left( {{\sigma ^{n - 1}}} \right) }^T}{S^{n - 1}}\left( {{\sigma ^{n - 1}}} \right) + {{\left( {{\sigma ^{n - 1}}} \right) }^T}{S^{n - 1}}\Delta \sigma } \,\nonumber \\&+ \,\Delta {\sigma ^T}{S^{n - 1}}{\sigma ^{n - 1}} - 2{\left( {{\sigma ^{n - 1}}} \right) ^T}\varepsilon \hbox {d}V \end{aligned}$$

(19)

We need to discretize the displacement field and stress field to get the displacement and stress of the node. Taking an example for 3D 8-nodes linear element, the discrete form is as follows:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\Delta u=N_q \Delta q}\\ {\Delta \sigma =N_p \Delta P} \\ {\varepsilon =\nabla N_q \Delta q} \\ \end{array} }} \right. \end{aligned}$$

(20)

where $\Delta u$ and $\Delta \sigma$ represent the incremental displacement field and incremental stress field of total elasticity, respectively. $N_p =\left[ {{\begin{array}{ll} {N_q }&{} \\ &{} {N_q } \\ \end{array} }} \right]$, $\hbox {Diag}\left( {N_q } \right) =\left[ {{\begin{array}{lll} {N_e }&{} {N_e }&{} {N_e } \\ \end{array} }} \right]$ and $N_e =\left[ {N_1 ,N_2 \ldots N_8 } \right]$

Substituting Eq. (20) into Eq. (19), we can obtain:

$$\begin{aligned} \prod \nolimits _\mathrm{G}^n= & {} \sum _{i=1}^j {\left[ \int _v {\Delta P^{T}\left( {N_p^T S^{n-1}N_p } \right) ^{i}\Delta P+2\Delta P^{T}\left( {N_p^T \nabla N_q } \right) ^{i}\Delta q}\right. } \nonumber \\&-\Delta q^{T}\left( {\nabla N_q^T C^{n-1}\nabla N_q } \right) ^{i}\Delta q\hbox {d}V \nonumber \\&+\,4\int _s {\left( {{\overline{T}} ^{T}N_q } \right) ^{i}\Delta q\hbox {d}S} \nonumber \\&+\,\int _V {\left( {\left( {\sigma ^{n-1}} \right) ^{T}S^{n-1}\left( {\sigma ^{n-1}} \right) } \right) } ^{i}+\left( {\left( {\sigma ^{n-1}} \right) ^{T}S^{n-1}N_P } \right) ^{i}\Delta P \nonumber \\&+\,\Delta P^{T}\left( {N_p^T S^{n-1}\sigma ^{n-1}} \right) ^{i}-2\left( {\left( {\sigma ^{n-1}} \right) ^{T}\nabla N_q } \right) ^{i}\Delta q\hbox {d}V \end{aligned}$$

(21)

where j indicates the number of total elements.

Consider $\Delta p$ and $\Delta q$ as two independent variables. By $\delta \prod _\mathrm{G} =0$, two Euler–Lagrange equations can be obtained:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\sum \limits _{i=1}^j {\left\{ {\int _V {\left( {N_p^T S^{n-1}N_P } \right) ^{i}\Delta P+\left( {N_p^T \nabla N_q } \right) ^{i}\Delta q\hbox {d}V} +\frac{1}{2}\int _V {\left[ {\left( {\sigma ^{n-1}} \right) ^{T}S^{n-1}N_P +N_P^T S^{n-1}\sigma ^{n-1}} \right] ^{i}\hbox {d}V} } \right\} =0} } \\ {\sum \limits _{i=1}^j {\left\{ {\int _V {\left( {N_P^T \nabla N_q } \right) ^{i}\Delta P-\left[ {\left( {\nabla N_q } \right) ^{T}C^{n-1}\nabla N_q } \right] ^{i}\Delta q\hbox {d}V+2\int _S {\left( {{\overline{T}} ^{T}N_q } \right) ^{i}\hbox {d}S-\int _V {\left[ {\left( {\sigma ^{n-1}} \right) ^{T}\nabla N_q } \right] ^{i}\hbox {d}V} } } } \right\} =0} } \\ \end{array} }} \right. \end{aligned}$$

(22)

In what follows, the superscript “i” will be dropped for clarity.

$$\begin{aligned} K_{11}^{n - 1}= & {} \int _V {N_P^T{S^{n - 1}}{N_p}\hbox {d}V} \nonumber \\ K_{12}^{n - 1}= & {} \int _V {N_P^T\nabla {N_q}\hbox {d}V} \nonumber \\ K_{21}^{n - 1}= & {} \int _V {N_P^T\nabla {N_q}\hbox {d}V} \nonumber \\ K_{22}^{n - 1}= & {} - \int _V {{{\left( {\nabla {N_q}} \right) }^T}{C^{n - 1}}\left( {\nabla {N_q}} \right) \hbox {d}V} \nonumber \\ F_1^n= & {} - \frac{1}{2}\int _V {{{\left( {{\sigma ^{n - 1}}} \right) }^T}{S^{n - 1}}{N_P} + N_P^T{S^{n - 1}}{\sigma ^{n - 1}}\hbox {d}V} \nonumber \\ F_\mathrm{{2}}^n= & {} - 2\int _S {{{\bar{T}}^T}{N_q}\hbox {d}S} + \int _V {{{\left( {{\sigma ^{n - 1}}} \right) }^T}\nabla {N_q}\hbox {d}V} \end{aligned}$$

(23)

The matrix simplified expressions of the two Euler–Lagrange equations are as follows:

$$\begin{aligned} \left[ {{\begin{array}{cc} {K_{\mathrm {11}}^{n-1} }&{}\quad {K_{12}^{n-1} } \\ {K_{21}^{n-1} }&{} \quad {K_{22}^{n-1} } \\ \end{array} }} \right] \left\{ {{\begin{array}{c} {\Delta P} \\ {\Delta q} \\ \end{array} }} \right\} =\left\{ {{\begin{array}{c} {F_1^n }\\ {F_2^n } \\ \end{array} }} \right\} \end{aligned}$$

(24)

The iteration in each increment has to be repeated until the following condition is satisfied:

$$\begin{aligned} \left\{ {{\begin{array}{l} {\frac{\left| {\Delta P^{n-1}} \right| }{\left| {\Delta P^{n}} \right| }\le \hbox {Tolerance 1}}\\ {\frac{\left| {\Delta q^{n-1}} \right| }{\left| {\Delta q^{n}} \right| }\le \hbox {Tolerance 2}} \\ \end{array} }} \right. \end{aligned}$$

(25)

Once stress condition of an element satisfies the proposed failure criteria, material property C is discounted according to the proposed stiffness degradation model shown in Table 1. This degradation in property will affect the distribution of stress in the damaged area. The redistributed stresses in the elasticity after damage can be calculated by performing the Newton–Raphson iteration again with updated material properties. The procedure will be repeated until no additional damage is predicted at the given load level.