Power transmission and suppression characteristics of stiffened Mindlin plate under different boundary constraints

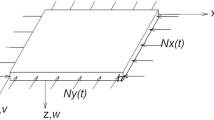
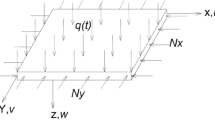
Abstract

The dynamic power transmission characteristics of a finite stiffened Mindlin plate subject to different boundary conditions are analytically studied. The stiffened plate is modeled as a coupled structure comprising a plate and stiffeners. Dynamic responses calculated by the analytical solutions are verified through comparison of the results with those generated using the finite element method. The computed results show that Mindlin plate and Timoshenko beam theory is more suitable for studying dynamic power of the stiffened plate over a broad frequency range than classical plate and beam theory. The stiffness and inertia characteristics of the Mindlin plate can be enhanced using the stiffeners, which can significantly affect the dynamic response, especially in low-frequency range. It can be also noticed that the stop band in the low-frequency range can become wider by increasing the number and dimension (height and width) of the stiffeners, so vibratory power of the stiffened Mindlin plate in the low-frequency range can be greatly reduced.

Appendix A

The elements of the amplitude coefficient matrix in Eq. (28) are as follows:

where,

$$\begin{aligned}&H_{11}^{(i)} =(\kappa GA_i \sigma _1 \gamma _m k_{ym}^2 -\rho _i A_i \omega ^{2}), \quad H_{12}^{(i)} =(\kappa GA_i \sigma _1 \gamma _m k_{ym}^2 -\rho _i A_i \omega ^{2})e^{\lambda _{2m} (x_i -x_{i-1} )}, \\&H_{13}^{(i)} =(\kappa GA_i \sigma _2 \gamma _m k_{ym}^2 -\rho _i A_i \omega ^{2}), \quad H_{14}^{(i)} =(\kappa GA_i \sigma _2 \gamma _m k_{ym}^2 -\rho _i A_i \omega ^{2})e^{\lambda _{4m} (x_i -x_{i-1} )}, \\&H_{15}^{(i)} =-\kappa GA_i \lambda _{5m} k_{ym} \gamma _m , \quad H_{16}^{(i)} =-\kappa GA_i \lambda _{6m} k_{ym} \gamma _m e^{\lambda _{6m} (x_i -x_{i-1} )}, \\&H_{21}^{(i)} =(\sigma _1 -1)\lambda _{1m} (GJ_i k_{ym}^2 \gamma _m +\rho _i J_i \omega ^{2}), \quad H_{22}^{(i)} =(\sigma _1 -1)\lambda _{2m} (GJ_i k_{ym}^2 \gamma _m +\rho _i J_i \omega ^{2})e^{\lambda _{2m} (x_i -x_{i-1} )}, \\&H_{23}^{(i)} =(\sigma _2 -1)\lambda _{3m} (GJ_i k_{ym}^2 \gamma _m +\rho _i J_i \omega ^{2}), \quad H_{24}^{(i)} =(\sigma _2 -1)\lambda _{4m} (GJ_i k_{ym}^2 \gamma _m +\rho _i J_i \omega ^{2})e^{\lambda _{4m} (x_i -x_{i-1} )}, \\&H_{25}^{(i)} =(GJ_i k_{ym}^3 +\rho _i J_i \omega ^{2}k_{ym} \gamma _m ), \quad H_{26}^{(i)} =(GJ_i k_{ym}^3 +\rho _i J_i \omega ^{2}k_{ym} \gamma _m )e^{\lambda _{6m} (x_i -x_{i-1} )}, \\&H_{31}^{(i)} =[(\sigma _1 -1)(EI_i k_{ym}^3 +\rho _i I_i \omega ^{2}k_{ym} )-\kappa GA_i \sigma _1 k_{ym} ], \\&H_{32}^{(i)} =[(\sigma _1 -1)(EI_i k_{ym}^3 +\rho _i I_i \omega ^{2}k_{ym} )-\kappa GA_i \sigma _1 k_{ym} ]e^{\lambda _{2m} (x_i -x_{i-1} )}, \\&H_{33}^{(i)} =[(\sigma _2 -1)(EI_i k_{ym}^3 +\rho _i I_i \omega ^{2}k_{ym} )-\kappa GA_i \sigma _2 k_{ym} ], \\&H_{34}^{(i)} =[(\sigma _2 -1)(EI_i k_{ym}^3 +\rho _i I_i \omega ^{2}k_{ym} )-\kappa GA_i \sigma _2 k_{ym} ]e^{\lambda _{4m} (x_i -x_{i-1} )}, \\&H_{35}^{(i)} =(\kappa GA_i -EI_i k_{ym}^2 \eta _m +\rho _i I_i \omega ^{2})\lambda _{5m} , \quad H_{36}^{(i)} =(\kappa GA_i -EI_i k_{ym}^2 \eta _m +\rho _i I_i \omega ^{2})\lambda _{6m} e^{\lambda _{6m} (x_i -x_{i-1} )}. \end{aligned}$$

The elements ${\varvec{\Pi }} _{01}$ and ${\varvec{\Pi }} _{(N+1)2}$ can be determined by the boundary conditions at the edges $x =0$ and $x=L_{x}$, and they are different for the different boundary conditions.