Toward understanding the self-adaptive dynamics of a harmonically forced beam with a sliding mass

Abstract

A mechanical system consisting of an elastic beam under harmonic excitation and an attached sliding body is investigated. Recent experimental observations suggest that the system passively (self-)adapts the axial location of the slider to achieve and maintain a condition of self-resonance, which could be useful in applications such as energy harvesting. The purpose of this work is to provide a theoretical explanation of this phenomenon based on an appropriate model. A key feature of the proposed model is a small clearance between the slider and the beam. This clearance gives rise to backlash and frictional contact interactions, both of which are found to be essential for the self-adaptive behavior. Contact is modeled in terms of the Coulomb and Signorini laws, together with the Newton impact law. The set-valued character of the contact laws is accounted for in a measure differential inclusion formulation. Numerical integration is carried out using Moreau’s time-stepping scheme. The proposed model reproduces qualitatively most experimental observations. However, although the system showed a distinct self-adaptive character, the behavior was found to be non-resonant for the considered set of parameters. Beside estimating the relationship between resonance frequency and slider location, the model permits predicting the operating limits with regard to excitation level and frequency. Finally, some specific dynamical phenomena such as hysteresis effects and transient resonance captures underline the rich dynamical behavior of the system.

Appendices

Appendix 1: Derivation of the beam’s equation of motion

In this appendix, the beam’s equation of motion Eqs. (1), (2) is derived from the formulation found in any standard textbook on vibrations of continua. The dynamic deformation v(x, t) of the beam in its autonomous configuration, in accordance with the theory specified in Sect. 2.1, is governed by

$$\begin{aligned}&\displaystyle \rho A\ddot{v}(x,t) + EI v^{\prime \prime \prime \prime }(x,t) = 0 \quad x\in ]0,\ell [\,, \end{aligned}$$

(8)

$$\begin{aligned}&\displaystyle v(0,t)=v^\prime (0,t)=v(\ell ,t)=v^\prime (\ell ,t) = 0\,. \end{aligned}$$

(9)

Introducing the base excitation $w_0(t)$ to the autonomous system, according to the considered connection between base and beam, can be modeled by adjusting the boundary conditions in Eq. (9) to,

$$\begin{aligned} {v(0,t)=w_0(t), \quad v^\prime (0,t)=v^\prime (\ell ,t) = 0,\quad v(\ell ,t)=w_0(t) \,.} \end{aligned}$$

(10)

Note that Eq. (8) remains unchanged.

A coordinate transform is now introduced,

$$\begin{aligned} {v(x,t) = w(x,t) + w_0(t)\,,} \end{aligned}$$

(11)

where the dynamic deformation v(x, t) is split into the imposed base displacement $w_0(t)$ and an elastic deformation w(x, t) measured from the time-dependent base location. To apply the transform, also the time and space derivatives of Eq. (11) are needed,

$$\begin{aligned} \ddot{v}(x,t)= & {} \ddot{w}(x,t) + \ddot{w}_0(t)\,, \end{aligned}$$

(12)

$$\begin{aligned} v^\prime (x,t)= & {} w^\prime (x,t) \,, \end{aligned}$$

(13)

$$\begin{aligned} v^{\prime \prime \prime \prime }(x,t)= & {} w^{\prime \prime \prime \prime }(x,t)\,. \end{aligned}$$

(14)

Substituting Eqs. (11)–(14) into Eq. (8) and Eq. (10) yields,

$$\begin{aligned} \rho A\left[ \ddot{w}_0 + \ddot{w}(x,t)\right] + EI w^{\prime \prime \prime \prime }(x,t)= & {} 0 \quad x\in ]0,\ell [\,,\\ w(0,t)=w^\prime (0,t)=w(\ell ,t)=w^\prime (\ell ,t)= & {} 0\,.\end{aligned}$$

This is identical to Eqs. (1), (2), already introduced in Sect. 2.1, which were used for the investigations in the present work. Note that Eq. (8) with boundary conditions (10) is fully equivalent with Eqs. (1), (2). Hence, either formulation can be utilized for the simulation of the coupled problem. Simulation results are therefore expected to be identical, in practice possibly limited by finite numerical precision.

Appendix 2: Contact laws

In this appendix, the contact laws are formulated, which are used to describe the dynamic contact interactions between beam and slider. For contact point $P_i$, the Signorini law relates the normal contact force $\lambda _{\mathrm {n},i}$ and the normal contact gap (relative displacement) $g_{\mathrm {n},i}$. The law and can be compactly written as

$$\begin{aligned} 0 \le \lambda _{\mathrm {n},i} \perp g_{\mathrm {n},i} \ge 0\,.\end{aligned}$$

(15)

Physically, this means that only compressive forces are allowed, and no penetration is permitted. Moreover, the symbol $\perp$ indicates the complementarity condition, i.e., that the force can admit nonzero values only if the contact is closed ($g_{\mathrm {n},i}=0$), and the force must be zero when the contact is open ($g_{\mathrm {n},i}>0$).

The one-dimensional Coulomb law relates the tangential gap velocity $\gamma _{\mathrm{t},i}$ and the tangential contact force $\lambda _{\mathrm {t},i}$,

$$\begin{aligned} {{\left\{ \begin{array}{ll} \text {sticking:} \quad \gamma _{\mathrm {t},i} = 0\quad \wedge &{} \quad \left| \lambda _{\mathrm {t},i}\right| < \mu \lambda _{\mathrm {n},i} \\ \text {slipping:} \quad \gamma _{\mathrm {t},i} \ne 0\quad \wedge &{} \quad \lambda _{\mathrm {t},i} = -\mu \lambda _{\mathrm {n},i} {\text {sign}}\left( \gamma _{\mathrm {t},i}\right) \end{array}\right. }\,.} \end{aligned}$$

(16)

Thus, the limit friction force $\mu \lambda _{\mathrm {n},i}$ depends on the normal contact force $\lambda _{\mathrm {n},i}$. The negative sign in the slipping case ensures that the friction force points in the opposite direction of the relative sliding velocity.

In the case of instantaneous impulses, the Newton impact law is considered. Normal and tangential impulses are denoted $\Lambda _{\mathrm {n},i}$ and $\Lambda _{\mathrm {t},i}$, respectively. The associated coefficients of restitution are $\epsilon _\mathrm {n}$ and $\epsilon _\mathrm {t}$. Velocities before and after the impulse marked by the superscripts $+$ and −. Applied to the normal contact, this leads to

$$\begin{aligned} 0 \le \Lambda _{\mathrm {n},i} \perp \gamma _{\mathrm {n},i}^+ + \epsilon _\mathrm {n}\gamma _{\mathrm {n},i}^- \ge 0\,,\end{aligned}$$

(17)

while for the tangential contact, this results in

$$\begin{aligned} {{\left\{ \begin{array}{ll} \text {sticking:} \quad \gamma _{\mathrm {t},i}^+ + \epsilon _\mathrm {t}\gamma _{\mathrm {t},i}^- = 0\quad \wedge &{} \quad \left| \Lambda _{\mathrm {t},i}\right| < \mu \Lambda _{\mathrm {n},i} \\ \text {slipping:} \quad \gamma _{\mathrm {t},i}^+ + \epsilon _\mathrm {t}\gamma _{\mathrm {t},i}^- \ne 0\quad \wedge &{} \quad \Lambda _{\mathrm {t},i} = -\mu \Lambda _{\mathrm {n},i} {\text {sign}}\left( \gamma _{\mathrm {t},i}^+ + \epsilon _\mathrm {t}\gamma _{\mathrm {t},i}^-\right) \end{array}\right. }\,.} \end{aligned}$$

(18)

It can generally be stated that the considered contact laws are commonly used for the modeling of various contact problems in engineering.

Fig. 16

Contact kinematics

Appendix 3: Contact kinematics

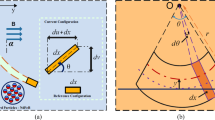
For each point $P_i$ of the four possible contact points of the slider, a corresponding closest point $P_{{\mathrm {b}},i}$ at the top or bottom surface of the beam can be identified (cf. Fig. 16). This point can be determined by finding the closest location $x_i^*$ on the beam’s axis in the Euclidian sense,

$$\begin{aligned} x_i^* = {\text {argmin}}\lbrace \Vert {}_{{\mathrm {N}}}\varvec{r}_{P_i} - {}_{{\mathrm {N}}}\varvec{r}_B(x)\Vert _2^2\rbrace \,.\end{aligned}$$

(19)

Herein, ${}_{{\mathrm {N}}}\varvec{r}_B(x) = \left[ \!\!\begin{array}{cc} x&w_0 + w(x)\end{array}\!\!\right] ^{\mathrm {T}}$ defines the position vector to the beam’s axis (with $w_0 + w(x)$ being the total deflection with respect to the inertial frame of reference), and ${}_{{\mathrm {N}}}\varvec{r}_{P_i} = {}_{\mathrm N}\varvec{r}_C + {}^{\mathrm {NS}}\varvec{A} {}_{~{\mathrm {S}}}\varvec{r}_{CP_i}$ is the position vector to the point $P_i$. The left subscript notation refers to the associated coordinate system. Three different coordinate systems are defined, namely the inertial coordinate system ${\mathrm {N}}$, the contact coordinate system ${\mathrm {C}}$ and the slider coordinate system ${\mathrm {S}}$ illustrated in Fig. 1b. The position vector of the center of mass C in the inertial frame of reference is ${}_{\mathrm N}\varvec{r}_C = \left[ \!\!\begin{array}{cc} x_C&z_C\end{array}\!\!\right] ^{\mathrm {T}}$. The matrix ${}^{\mathrm {NS}}\varvec{A}$ takes care of the transformation between slider and inertial frame of reference, and it is defined as,

$$\begin{aligned} {}^{\mathrm {NS}}\varvec{A} = \left[ \!\!\begin{array}{cc} \cos \varphi &{} \sin \varphi \\ -\sin \varphi &{} \cos \varphi \end{array}\!\!\right] \,,\end{aligned}$$

(20)

depending on the slider rotation $\varphi$. The contact points $P_1$ through $P_4$ have the coordinate vectors,

$$\begin{aligned} {}_{~{\mathrm {S}}}\varvec{r}_{CP_1} = \left[ \!\!\begin{array}{c} -\frac{b_1}{2}\\ d + \frac{R}{2}\end{array}\!\!\right] ,\quad {}_{~{\mathrm {S}}}\varvec{r}_{CP_2} = \left[ \!\!\begin{array}{c} -\frac{b_1}{2}\\ d - \frac{R}{2}\end{array}\!\!\right] ,\quad {}_{~{\mathrm {S}}}\varvec{r}_{CP_3} = \left[ \!\!\begin{array}{c} +\frac{b_1}{2}\\ d - \frac{R}{2}\end{array}\!\!\right] ,\quad {}_{~\mathrm S}\varvec{r}_{CP_4} = \left[ \!\!\begin{array}{c} +\frac{b_1}{2}\\ d + \frac{R}{2}\end{array}\!\!\right] \,,\end{aligned}$$

(21)

in the slider coordinate system.

Once the locations $x_i^*$ are found, the contact gap vectors are expressed as

$$\begin{aligned} {}_{{\mathrm {C}}}\varvec{g}_i = {}^{\mathrm {CN}}\varvec{A}\left( {}_{\mathrm {N}}\varvec{r}_{\mathrm{P}_i} - {}_{\mathrm {N}}\varvec{r}_{P_{\mathrm{b},i}}\right) = \left[ \!\!\begin{array}{c} g_{\mathrm {n},i}\\ g_{\mathrm {t},i}\end{array}\!\!\right] \,,\end{aligned}$$

(22)

where ${}_{\mathrm {N}}\varvec{r}_{P_{\mathrm{b},i}}$ reads

$$\begin{aligned} {}_{\mathrm {N}}\varvec{r}_{P_{\mathrm{b},i}} = {}_{\mathrm {N}}\varvec{r}_{B}(x^*_i) + \xi _i\frac{ r}{\sqrt{1+\tan ^2\theta }}\left[ \!\!\begin{array}{c} -\tan \theta \\ 1\end{array}\!\!\right] \,.\end{aligned}$$

(23)

Herein, $\tan \theta$ is related to the beam’s slope at $x^*_i$ by $\tan \theta = w^\prime (x^*_i)$. The parameter $\xi _i$ is $+1$ for $i\in \lbrace 1,4\rbrace$ (top surface), and $-1$ for $i\in \lbrace 2,3\rbrace$ (bottom surface). The rotation matrix ${}^{\mathrm {CN}}\varvec{A}$ in Eq. (22) reads,

$$\begin{aligned} {}^{\mathrm {CN}}\varvec{A} = \xi _i\left[ \!\!\begin{array}{cc} -\sin \theta &{} \cos \theta \\ -\cos \theta &{} -\sin \theta \end{array}\!\!\right] \,,\end{aligned}$$

(24)

and accounts for the transformation between inertial and contact coordinate systems.

The relative velocity ${}_{{\mathrm {C}}}\varvec{\gamma }_i = \frac{{\mathrm {d}}{}_{{\mathrm {C}}}\varvec{g}_i}{{\mathrm {d}}t}$ can be derived from Eq. (22). The result can be split up as

$$\begin{aligned} {}_{{\mathrm {C}}}\varvec{\gamma }_i = \left[ \!\!\begin{array}{c} \gamma _{\mathrm {n},i}\\ \gamma _{\mathrm {t},i}\end{array}\!\!\right] = \varvec{W}_i^{\mathrm {T}}\varvec{u} + \varvec{w}_i\,,\end{aligned}$$

(25)

where the first term accounts for the contribution of the generalized velocity, and involves the matrix of generalized contact force directions $\varvec{W}_i^{\mathrm {T}}= \frac{\partial {}_{{\mathrm {C}}}\varvec{g}_i}{\partial \varvec{q}^{\mathrm {T}}}$. The second term in Eq. (25) accounts for the explicit time dependence of the relative velocity with $\varvec{w}_i = \frac{\partial {}_{{\mathrm {C}}}\varvec{g}_i}{\partial t}$. In the considered model, this term stems from the base excitation. The algebraic forms of these derivatives are not presented for brevity.

Appendix 4: Time stepping

To discretize the measure differential inclusion, we applied the common Moreau time-stepping scheme with a constant time step $\Delta t$. Therefore, the generalized coordinates $\varvec{q}^{{\mathrm {M}}}$ are first evaluated at the midpoint between the previous and the next time step. This is achieved by taking an Euler step, $\varvec{q}^{{\mathrm {M}}} = \varvec{q}^{{\mathrm {B}}} + \varvec{u}^{{\mathrm {B}}}\frac{\Delta t}{2}$. Quantities at the beginning, the midpoint and the end of the time step are denoted by a superscript ${\mathrm {B}}$, ${\mathrm {M}}$ and ${\mathrm {E}}$, respectively.

The contact kinematics is then evaluated at the midpoint. The set $\mathcal I_{{\mathrm {C}}}$ of active contact points is identified as $\mathcal I_{{\mathrm {C}}} = \lbrace j\vert g_{\mathrm {n},j}\le 0\rbrace$. Let $n_{{\mathrm {C}}}$ be the number of active contact points. For each active contact point, the kinematical quantities are then evaluated and assembled in the matrix $\varvec{W} = \left[ \!\!\begin{array}{ccc} \varvec{W}_1&\cdots&\varvec{W}_{n_{\mathrm C}}\end{array}\!\!\right]$ and the vector $\varvec{w} = \left[ \!\!\begin{array}{ccc} \varvec{w}_1^{\mathrm {T}}&\cdots&\varvec{w}_{n_{{\mathrm {C}}}}^{\mathrm {T}}\end{array}\!\!\right] ^{\mathrm {T}}$.

In accordance with the Moreau scheme, the velocity vector $\varvec{u}^{{\mathrm {E}}}$ at the end of the time step is defined by the second stepping equation $\varvec{u}^{{\mathrm {E}}} = \varvec{u}^{{\mathrm {B}}} + \varvec{M}^{-1}\left[ \varvec{h}\left( \varvec{q}^{{\mathrm {M}}},\varvec{u}^{\mathrm M},t^{{\mathrm {M}}}\right) \Delta t + \varvec{W}\left( \varvec{q}^{\mathrm M}\right) \varvec{P}\right]$, where $\varvec{P}$ is the unknown contact percussion vector. The contact percussions and the gap velocities need to satisfy the set-valued contact laws. The computation of the compatible contact percussions is addressed in the next subsection. Upon computation of the contact percussions and velocities $\varvec{u}^{{\mathrm {E}}}$, the coordinates $\varvec{q}^{{\mathrm {E}}}$ at the end of the time step are finally updated using $\varvec{q}^{{\mathrm {E}}} = \varvec{q}^{{\mathrm {M}}} + \varvec{u}^{{\mathrm {E}}}\frac{\Delta t}{2}$.

1.1 Reformulation of the contact laws

The set-valued contact laws are enforced by solving an inclusion problem $-\left( \varvec{\gamma }^{{\mathrm {E}}} + \varvec{\epsilon } \varvec{\gamma }^{{\mathrm {B}}} \right) \in \mathcal N_{\mathcal C}\left( \varvec{P}\right)$, which ensures the compatibility of the contact velocity $\varvec{\gamma } = \left[ \!\!\begin{array}{ccc} \varvec{\gamma }_1^{\mathrm {T}}&\cdots&\varvec{\gamma }_{n_{{\mathrm {C}}}}^{\mathrm {T}}\end{array}\!\!\right] ^{\mathrm {T}}$ at the beginning and at the end of the time step, and the contact percussion $\varvec{P}$. This compact formulation contains both contact and impact laws, and involves the matrix $\varvec{\epsilon }= {\text {bdiag}}\lbrace \varvec{\epsilon }_i\rbrace$ with $\varvec{\epsilon }_i = {\text {diag}}\lbrace \epsilon _{\mathrm {n},i},\epsilon _{\mathrm {t},i}\rbrace$, and the convex set $\mathcal C = \mathcal S_1 \times \cdots \times \mathcal S_{n_{{\mathrm {C}}}}$ with $S_i = \mathbb R_0^+ \times \left[ -\mu P_{\mathrm {n},i},\mu P_{\mathrm {n},i}\right]$. By substituting the stepping equation into the inclusion problem, one obtains an implicit algebraic inclusion problem in the unknown contact percussions $\varvec{P}$,

$$\begin{aligned} -\left( \varvec{G}\varvec{P} + \varvec{c} \right) \in \mathcal N_{\mathcal C}\left( \varvec{P}\right) \,,\end{aligned}$$

(26)

with the so-called Delassus matrix $\varvec{G} = \varvec{W}^{\mathrm {T}}\varvec{M}^{-1}\varvec{W}$ and the vector $\varvec{c} = \left( \varvec{I} + \varvec{\epsilon }\right) \left( \varvec{W}^{\mathrm {T}}\varvec{u}^{{\mathrm {B}}} + \varvec{w}\right) + \varvec{W}^{\mathrm {T}}\varvec{M}^{-1}\varvec{h}\Delta t$.

1.2 Computation of the contact percussions

In the convex analysis framework, the inclusion problem can be re-written as an implicit proximal point equation $\varvec{P} = {\text {prox}}_{\mathcal C}\left[ \varvec{P} - \varvec{R}^{-1}\left( \varvec{ G}\varvec{P} + \varvec{c}\right) \right]$ with the metric matrix $\varvec{R} = \varvec{R}^{\mathrm {T}}> \varvec{0}$. This corresponds to an augmented Lagrangian approach. Popular solvers for this equation include the Jacobi and the Gauss–Seidel relaxation method, both of which have been implemented. Both methods involve a sequential application of basic proximal point operations on the subsets of $\mathcal C$. The relevant operations are

$$\begin{aligned} {\text {prox}}_{\mathbb R_0^+}(\xi ) = {\left\{ \begin{array}{ll} \xi &{} \xi \ge 0\\ 0 &{} \xi <0\end{array}\right. }\,,\end{aligned}$$

(27)

for the unilateral contact and

$$\begin{aligned} {\text {prox}}_{[-a,a]}(\xi ) = {\left\{ \begin{array}{ll} a &{} \xi > a\\ \xi &{} -a \le \xi \le a\\ -a &{} \xi <-a\end{array}\right. }\,,\end{aligned}$$

(28)

for the frictional contact.