1 Introduction

Advancements in computing hardware and software have enabled a comprehensive analysis of complicated flow fields using computational fluid dynamics (CFD). However, the high nonlinearity inherent in both Navier–Stokes and Euler equations leads to an extensive number of degrees of freedom (DOF), resulting in a huge amount of computational time and memory. To overcome such limitations, various model order reductions (MOR) have been proposed.

MOR aims at converting a higher dimensional representation into a lower dimensional one while preserving the main feature of the original. Over the past decades, MOR schemes, such as proper orthogonal decomposition (POD) [1, 2], balanced method [3], and empirical Gramian [4], have been proposed. POD is one of the most widely used approaches, owing to its robustness and optimality [5]. POD, also known as the Karhunen–Loéve theorem or principal component analysis, was introduced by Lumley [1] to analyze a turbulent flow field. This was later improved by Sirovich [2] using the snapshot method. POD extracts the reduced basis, referred to as the POD mode, using singular value decomposition (SVD) on the snapshot. An efficient surrogate representation is then constructed by combining a finite, small number of POD modes that will contain the majority of properties.

There are two approaches to MOR: intrusive and nonintrusive. POD in an intrusive MOR is combined with Galerkin projection [6,7,8], where the governing equation is projected onto the reduced subspace. Because of the dependence on the governing equation, multiparametric analysis becomes tedious when the specific CFD algorithm is not explicitly established [9]. To address these difficulties, a nonintrusive MOR (NIMOR) was proposed. NIMOR is a purely data-driven approach based on high-fidelity analysis results without knowledge of the governing equation. Similar to the intrusive method, POD for NIMOR extracts reduced bases. However, additional treatment will be performed in the POD mode or coefficient to approximate the full order model (FOM), rather than projecting the higher dimensional representation.

NIMOR utilizes the latest developments in machine-learning techniques. Gaussian process regression (GPR) has been used by several researchers [10, 11] owing to its simplicity and decent performance. However, GPR is known to be more inaccurate than the latest machine-learning techniques [12]. An artificial neural network (ANN) was employed for NIMOR, including a simple multilayer perceptron [13,14,15,16,17], long short-term memory networks [18,19,20], and generative adversarial networks [21, 22].

Attempts to replace POD as a MOR method are found. One of the most popular choices is the autoencoder for nonlinear MOR [20, 23,24,25]. Extension of the conventional autoencoder, such as SINDy autoencoder [26], and combined POD-autoencoder methodology [27] were investigated. Using the autoencoders, parametric MOR was attempted by identifying its latent space [28, 29]. Other methods include the physics-informed neural networks (PINN). In PINN, neural networks are designed to be universal function approximators to describe the partial differential equations [30, 31].

In this study, an ANN exploiting unsupervised learning method based on the modified Nouveau variational autoencoder (mNVAE) was adopted. Unlike supervised learning method, an ANN exploiting unsupervised learning method generates the result based on the pattern and feature of the given dataset, which is learned without a label. Autoencoder [32], VAE [33], and generative adversarial network (GAN) [34] are the most recognized unsupervised learning approaches. Several variations of these networks have been proposed to improve the performance. Based on pattern searching and clustering, they are applied to diverse tasks, including dimensionality reduction. In particular, they are widely used for image denoising, restoration, generating novel realistic data via interpolation, super-resolution of images, and anomaly detection [35,36,37,38,39,40].

Among generative neural networks, VAE is known to be much more stable during training than GAN. During the training of GAN, phenomena such as mode collapse and imbalance of the generator/critic network performance may occur. A situation referred to as posterior collapse occurs in vanilla VAE. This issue was alleviated by applying a technique known as Kullback–Leibler divergence (KL divergence) annealing [41,42,43,44]. Deep hierarchical VAE such as Ladder VAE (LVAE) [42] and Nouveau VAE (NVAE) [44] were proposed to stack multiple layers in VAE for a better formulation. These approaches force the encoder and decoder networks in VAE to produce analogous distribution results.

Several attempts have been made to apply unsupervised learning method to MOR. Phillips et al. [45] developed a reduced-order model (ROM) known as the SVD-autoencoder in which SVD was operated on the input of the autoencoder. Xu et al. [46] developed a multistage MOR for parametric estimation of the flow field based on a coarsely constructed overset grid and convolutional autoencoder. However, autoencoders are known to exhibit inferior performance because of their sparse latent space and wide range of latent variables [47]. Lee et al. [21] employed WGAN-GP and POD for unobserved parametric values of the flow field. Although WGAN-GP is known for generating “sharper” details, it is also known for slower and unstable training. In contrast, VAE is characterized by stable and fast training. The authors found that VAE would also be capable of generating “sharp” details if the dataset was one-dimensional (1D). Cheng et al. [48] developed a hybrid VAE-GAN for parameterized flow analysis. However, its applications were limited to a small number of DOFs and VAE was not optimal for MOR use when the number of DOF exceeded a few hundred thousand. The reconstruction error of VAE will become significantly large, and stability during training will degrade owing to the regularizing term, KL divergence.

In this study, a combination of POD and variation to VAE, referred to as the modified NVAE (mNVAE), was adopted to construct a nonintrusive parametric MOR (pMOR) for the analysis of FSI. The present methodology is henceforth referred to as POD-mNVAE. POD is used to reduce the order of the higher dimensional representation, and mNVAE will be used for interpolation. Two examples were examined: the flow field around a plunging airfoil, flow around a highly nonlinear FSI phenomenon, and limit cycle oscillation (LCO) of an airfoil. The computational time and accuracy were evaluated for both examples, and a comparison with those previously proposed was performed.

The remainder of this paper is organized as follows. Section 2 presents the formulation of POD and modification to its snapshot matrix for parametric information. The formulation of VAE and modifications are provided in Sect. 3. Section 4 consists of the assumptions and procedures to execute POD-mNVAE. Section 5.1 demonstrates the applications of POD-mNVAE on two FSI objects. A comparison against previously proposed POD-based ANN methods is also presented. The conclusion and a relevant discussion are presented in Sect.6.

2 Proper orthogonal decomposition (POD)

The proposed scheme first constructs a lower dimensional representation of FOM using a reduced-order basis. The snapshot matrix is an ensemble of FOM analysis results. On the snapshot matrix, POD extracts the characteristics of a higher dimensional FOM using SVD. Using SVD, the POD modes are collected based on the dynamic energy ratio. Then, the POD modes are used as the basis vectors for MOR.

A snapshot matrix with a size of \(N\times S\) is expressed in Eq. (1). Here, v denotes the physical variable of interest from the flow field, N corresponds to the number of DOF, and S corresponds to the number of time steps as follows:

$$\begin{aligned} \varvec{W}= \left[ \begin{matrix} v_{1}^{(1)} &{} v_{1}^{(2)} &{} \cdots &{} v_{1}^{(S-1)} &{} v_{1}^{(S)} \\ v_{2}^{(1)} &{} v_{2}^{(2)} &{} \cdots &{} v_{2}^{(S-1)} &{} v_{2}^{(S)} \\ \vdots &{} \vdots &{} \ddots &{} \vdots &{} \vdots \\ v_{N-1}^{(1)} &{} v_{N-1}^{(2)} &{} \cdots &{} v_{N-1}^{(S-1)} &{} v_{N-1}^{(S)} \\ v_{N}^{(1)} &{} v_{N}^{(2)} &{} \cdots &{} v_{N}^{(S-1)} &{} v_{N}^{(S)} \\ \end{matrix}\right] \end{aligned}$$
(1)

The snapshot matrix was modified to accommodate parametric variations. The snapshot matrices for each parametric value are concatenated in the row direction. A single appended snapshot matrix, \(W_{total}\) will be constructed, and it contains parametric as well as spatio-temporal information. Equation (2) represents the snapshot matrix modified by parameter \(N_{p}\) in which the second superscript denotes the parameter as follows:

$$\begin{aligned} \varvec{W}_{{\varvec{total}}}=\left[ \left[ \begin{matrix} v_{1}^{(1,1)} &{} \cdots &{} v_{1}^{(S, 1)} \\ \vdots &{} \ddots &{} \vdots \\ v_{N}^{(1,1)} &{} \cdots &{} v_{N}^{(S, 1)} \end{matrix}\right] \cdots \right. \\ \left. \left[ \begin{matrix} v_{1}^{\left( 1, N_{p}\right) } &{} \cdots &{} v_{1}^{\left( S, N_{p}\right) } \\ \vdots &{} \ddots &{} \vdots \\ v_{N}^{\left( 1, N_{p}\right) } &{} \cdots &{} v_{N}^{\left( S, N_{p}\right) } \end{matrix}\right] \right] \end{aligned}$$
(2)

After the construction of the snapshot matrix was completed, SVD was performed. Then, the POD modes \(\phi _{i}\) were extracted using the process in Eq. (3) as follows:

$$\begin{aligned} \begin{aligned} \varvec{C}=\varvec{W}^{T}\varvec{W} \\ \varvec{CV}=\lambda \varvec{V}\;\\ \phi _{i}=\frac{1}{\sqrt{\lambda _{i}}}\varvec{W}V_{i} \end{aligned} \end{aligned}$$
(3)

The number of POD modes to be considered for MOR is determined by the energy ratio \(\lambda _i\). The accumulated energy ratio E is defined by Eq. (4). The number of POD modes, \(N_{m}\), is determined by the total energy considered, E:

$$\begin{aligned} E=\frac{ \sum \limits _{{i=1}}^{N_m} \lambda _{i}}{\sum \limits _{{i=1}}^{N}\lambda _{i}} \end{aligned}$$
(4)

The POD coefficients for time t and parameter p were obtained by projecting the FOM solutions onto the space generated by the POD modes. The variable of interest is then generated by the combination of POD coefficients and modes. Then, the original variable of interest, \(v^* \approx v\), is obtained by the sum of the averaged value, \({\bar{v}}\), and perturbations, \({\hat{v}}\), as expressed in Eq. (6) as follows:

$$\begin{aligned} a_{i}(t,p)= & {} \varvec{W}\phi _{i}^{T} \end{aligned}$$
(5)
$$\begin{aligned} v^{*}(x,t,p)= & {} {\bar{v}}(x)+{\hat{v}}(x,t,p) \nonumber \\= & {} {\bar{v}}(x)+\sum _{i=1}^{N_{m}}a_{i}(t,p)\phi _{i}(x) \end{aligned}$$
(6)

POD modes \(\Phi _{i}(x)\) in Eq. (6) contain spatial information that is invariant with respect to the parameter and time, whereas POD coefficients, \(a_{i}(t, p)\), contain the parametric and temporal information invariant with respect to the location. Naturally, POD coefficients comprise temporal information appended with respect to the parameter. These are decomposed later for mNVAE training.

3 Modified Nouveau variational autoencoder (mNVAE)

3.1 Variational autoencoder (VAE)

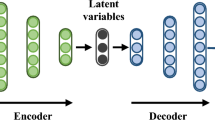
The current neural network, mNVAE, is an improved version of the VAE. VAE largely comprises two components: an encoder and decoder. The output of the encoder is expressed by the mean \(\mu\) and the variance \(\sigma\) which will be used to generate the latent code, z. VAE aims to infer an intractable posterior distribution efficiently. As it is difficult to determine the true posterior, \(p\left( z\mid x\right)\), VAE utilizes an approximate posterior, \(q\left( z\mid x\right)\). Regarding the structure of VAE, \(q\left( z\mid x\right)\) indicates an encoder or an inference network. \(p\left( x \mid z\right)\) denotes the decoder network. A typical structure of VAE is found in Fig. 1.

Fig. 1
figure 1

Structure of a typical VAE

Full size image

The objective function of VAE was formulated as expressed in Eq. (7). The first term denotes the negative log-likelihood that operates as a reconstruction error. It is designed to minimize the discrepancy between the given input and the generated output. The second term is KL divergence, which is the distance between two distributions. KL divergence forces the approximate posterior to become closer to the prior, p(z). During the optimization process, KL divergence acts as a regularization term:

$$\begin{aligned} \min [ -\mathbb {E}_{q(z \mid x)}[\log p(x \mid z)]+ D_{K L}(q(z \mid x) \Vert p(z)) ] \end{aligned}$$
(7)

Usually, KL divergence term in the loss function can be integrated analytically [33]. The reconstructed error on the other hand, is not directly differentiable since z is sampled from \(\mu\) and \(\sigma\). To enforce it to be differentiable, reparameterization trick was adopted for the latent code sampling. First, Gaussian-sampled random noise, \(\epsilon\) was introduced to the latent code. The latent code z, was formulated by \(\mu\), \(\sigma\), and \(\epsilon\), so that, \(z=\mu +(\sigma \times \epsilon )\). The new z enabled reconstruction loss to be differentiable by Monte Carlo method. Thus, the reconstruction loss would be backpropagated.

3.2 Hierarchical network

The conventional VAE is constrained to a shallow model with only a few layers of stochastic latent variables. Such constraints result in a restrictive mean-field approximation and degrade the VAE performance [42]. Deep hierarchical VAE such as LVAE [42] and NVAE [44] have been proposed to overcome these limitations. The ladder network connects the inference and generative networks via bidirectional information transfer [49]. The network structure is shown in Fig. 2.

Fig. 2
figure 2

Structure of deep hierarchical VAE

Full size image

The latent variables in the deep hierarchical VAE are partitioned. The latent variables are sampled from the layers in both bottom-up and top-down network as shown in Fig. 2. Especially, to generate ith latent variable, \(z_i\), ith layer in the top-down network is used. The ith layer in the top-down network originates from predecessing latent variable, \(z_{i+1}\), thus the network contains top-down information. Similarly, \(z_i\) also requires ith layer in the bottom-up network.

Since both bottom-up and top-down layers are used to sample latent variables in each layer, bidirectional information will be shared. Conventional deep VAE lack long-range correlations as first few encoder layers affect very little on the output. For the ladder VAEs, even the first encoder layer will be used to sample latent variable enabling better quality latent variables.

The latent variables are separated into L groups: \(z=\left\{ z_{1}, z_{2}, z_{3}, \cdots , z_{L}\right\}\). The prior and posterior can be fully factorized, as expressed in Eq. (8) and subsequently specified as expressed in Eq. (9), using a Gaussian distribution for each group:

$$\begin{aligned} p(z)= & {} p\left( z_{L}\right) \prod _{i=1}^{L-1} p\left( z_{i} \mid z_{i+1}\right) \nonumber \\ q(z \mid x)= & {} q\left( z_{1} \mid x\right) \prod _{i=2}^{L} q\left( z_{i} \mid z_{i-1}\right) \end{aligned}$$
(8)
$$\begin{aligned} p(z_{i} \mid z_{i+1})= & {} \mathcal {N}(z_{i} \mid \mu (z_{i+1}), \sigma ^{2}(z_{i+1}))\nonumber \\ p(z_{L})= & {} \mathcal {N}(z_{L} \mid 0, I)\nonumber \\ q(z_{i} \mid z_{i-1})= & {} \mathcal {N}(z_{i} \mid \mu (z_{i-1}), \sigma ^{2}(z_{i-1}))\nonumber \\ q(z_{1} \mid x)= & {} \mathcal {N}(z_{1} \mid \mu (x), \sigma ^{2}(x)) \end{aligned}$$
(9)

From the factorized distribution, the objective is specified in Eq. (10) in which the KL divergence is obtained individually. As aforementioned, KL divergence will force the approximate posterior to approach the prior. Therefore, splitting the KL divergence into groups will lead to bidirectional information transfer between the inference and generative networks. A detailed explanation of the ladder network for the VAE can be found in [42]:

$$\begin{aligned} \begin{aligned} \min [ -\mathbb {E}_{q(z \mid x)}[\log p(x \mid z)]+ D_{K L}(q(z \mid x) \Vert p(z))\\ +\sum _{i=1}^{L-1} \mathbb {E}_{q(z_{<i} \mid x)}[D_{K L}(q(z_{i} \mid z_{<i}, x) \Vert p(z_{i} \mid z_{>i}))]] \end{aligned} \end{aligned}$$
(10)

3.3 Modified NVAE (mNVAE)

The present ANN, mNVAE, is a modified version of NVAE [44] for improved accuracy when used with a 1D transient dataset. The network comprises 1D convolutional layers for the temporal continuity of the transient dataset. Instead of the conventional binary cross-entropy KL divergence, which is widely used for VAE, a hybrid weighted mean squared error KL divergence loss function is considered. The hybrid weighted loss function empirically shows better results regarding continuous data. The loss function for mNVAE is expressed as in Eq. (11) as follows:

$$\begin{aligned} \begin{aligned} \min _{\phi , \theta } [\alpha MSE(x, {\tilde{x}})+ \beta D_{K L}(q(z \mid x) \Vert p(z))\\ +\sum _{i=1}^{L-1}\alpha MSE(x, {\tilde{x}})[\beta D_{K L}(q(z_{i} \mid z_{<i}, x) \Vert p(z_{i} \mid z_{>i}))]] \end{aligned} \end{aligned}$$
(11)

In Eq. (11), the reconstruction loss, \(\mathbb {E}\), is replaced by the mean squared error, MSE, between the input and output datasets. \(\alpha\) and \(\beta\) denote the weight functions of MSE and KL divergence losses, respectively. The weight ratio for each loss function was set as approximately 1,000 \(\alpha : \beta _{target}\approx 1,000:1\). For the mNVAE, KL annealing [41] is used, and \(\beta\) is expressed as in Eq. (12) as follows:

$$\begin{aligned} \beta = {\left\{ \begin{array}{ll} 1\times 10^{-4}\beta _{target} &{}\hbox { if epoch}\ <0.3n_{epochs}\\ \beta _{target}\frac{epoch}{n_{epochs}}&{}\text {if epoch } >0.3n_{epochs} \end{array}\right. } \end{aligned}$$
(12)

KL annealing prevents a posterior collapse in which some of latent variables become inactive. At the start of training, the weight for KL divergence will be quite small and will act like an autoencoder. Then, the weight will be increased gradually introducing regularization term, resulting in a VAE. For interpolation in the latent space, spherical linear interpolation (slerp) is considered. Gaussian sampling forms latent space of mNVAE into a multi-dimension hypersphere. Linear interpolation within a hypersphere usually results in poor interpolation quality, where the interpolated vector length is ignored. Instead, linear interpolation along the sphere will be performed. By slerp interpolation, arc length will be interpolated linearly.

4 Framework

The proposed scheme makes the following two assumptions:

  1. 1.

    A sufficient number of the samplings is performed within the parametric space.

  2. 2.

    Change in the physical dynamics should be semi-continuous, i.e., no divergence or shock within the parametric space.

These assumptions are adopted such that the combination of POD modes may be sufficient to represent the flow field. The second assumption signifies that there should not exist any drastic change in the physical properties with respect to the parameter. Discontinuity in the phenomenon will lead to incapability of using POD modes semi-universally within the parametric space. Since the proposed scheme does not interpolate POD modes, the physical properties will be semi-continuous to ensure accuracy of the interpolation. Otherwise, collected POD modes will not be sufficient to construct the target flow field. A further explanation is discussed in Lee et al. [21].

4.1 Present POD approach

The snapshot matrix for the variable of interest, \(\varvec{W}_{p_{j}}\), are collected from the FOM result for each parameter. The snapshot matrices for each parameter are appended in the row direction to create a single snapshot matrix \(\varvec{W}_{total}=\left[ \varvec{W}_{p_{1}}, \varvec{W}_{p_{2}}, \cdots , \varvec{W}_{p_{N_{p}}}\right]\). Then, SVD is performed on \(\varvec{W}_{total}\) to obtain the spatially dependent POD modes, \(\phi _{i}\). The corresponding POD coefficients, \(a_{i}\), in contrast, are temporally and parametrically dependent. Based on the aforementioned assumptions, the POD modes are quasi-universal with respect to the parameter. The POD coefficients are then partitioned with regard to the parameter, as in Eq. 13:

$$\begin{aligned} \begin{aligned} \alpha _{i}= \left\{ \left( \alpha _{1}^{1}, \alpha _{2}^{1}, \cdots , \alpha _{S}^{1}\right) , \cdots , \left( \alpha _{1}^{N_{p}}, \alpha _{2}^{N_{p}}, \cdots , \alpha _{S}^{N_{p}}\right) \right\} \end{aligned} \end{aligned}$$
(13)

The number of POD modes and coefficients was selected based on the energy ratio. By aligning the energy ratio of the POD modes to its size, the higher POD modes will exhibit a small value. These higher modes are neglected for MOR construction, and only a few lower modes are used.

4.2 Present mNVAE

The mNVAE encoder and decoder blocks are shown in Fig. 3. The current network comprises a bidirectional structure: bottom-up or top-down. The entire network of mNVAE comprises the blocks shown in Fig. 3. The encoder block contained a series of SN-LeakyReLU-dropout-Conv1D layers, where SN denotes the spectral normalization and Conv1D represents a 1D convolutional layer. The decoder block comprises an identical block, except for TransConv1D. TransConv1D is a transposed version that replaces Conv1D in the encoder for reconstruction. The numbers in parentheses next to Conv1D and TransConv1D layers are the kernel sizes. The dropout rates for the encoder and decoder were set as 0.2 and 0.1, respectively. This was designed to prevent overfitting and the SN layer was designed to stabilize the training process. Conv1D was employed to consider the temporal continuity of the POD coefficients.

Fig. 3
figure 3

Block construction in mNVAE

Full size image

4.3 Training mNVAE and the flow field reconstruction

POD coefficients \(a_i\) are collected for \(N_{m}\times N_{p}\) sets with a length of S time steps. The input dataset for mNVAE comprises 20 POD coefficients per network. The batch size for the training is denoted by \(N_{b}\). The input dataset was reshaped into \(\left( N_{b}, S, 20\right)\) and normalized to [0,1] for each POD coefficient. After the encoder, the shape of the latent code becomes \(\left( N_{b}, N_{l}\right)\), where \(N_{l}\) denotes the latent dimension size. The change in the data dimension in mNVAE is expressed in Eq. (14) as follows:

$$\begin{aligned} \left( N_{b}, S, 20\right) \xrightarrow {\text {encoder}}\left( N_{b}, N_{l}\right) \xrightarrow {\text {decoder}}\left( N_{b}, S, 20\right) \end{aligned}$$
(14)

mNVAE is trained for POD coefficient interpolation, as shown in Algorithm 1. In Algorithm 1, a standard Adam optimizer is used and the ladder network architecture is adopted.

figure a

The training process of the mNVAE can be divided into two parts: encoder and decoder training. First, the input dataset x is the normalized POD coefficient for each POD mode. In Algorithm 1, \(N(a^m)\) denotes the normalization function of the POD coefficient. The normalized POD coefficient is provided to the first layer of L-layer encoder \(q^{enc}_{\phi ,1}\). The first encoder layer outputs \(u_1\) and transforms it into \(\mu _{q,1}, \sigma _{q,1}\). Then, for the remaining encoder layers, the output of the former layer, \(u_{j-1}\), is provided as the input. Finally, the \(L_{th}\) encoder layer, the latent code \(z_L\), is formulated by the mean and variance \(\mu _{q,L}, \sigma _{q,L}\). In the formulation of the latent code, a Gaussian normally distributed random number, \(\varepsilon\), is added. The decoder is trained in a similar manner, where the input of the first decoder layer is substituted by \(z_L\). A detailed explanation of the training of a VAE using a ladder network can be found in [42, 44].

Beyond the encoder, the latent variables are distributed over the latent dimension. Since Gaussian random noise was introduced, certain latent codes may not accurately represent the target POD coefficient. Therefore, an adequate latent code is sought for each parameter and coefficient prior to interpolation. Latent code search is performed by first providing the input dataset to the encoder. Latent code \(z_{L}\) is sampled from the encoder and then fed to the decoder. The discrepancy between the input and output of mNVAE is estimated. If the discrepancy is sufficiently small, \(z_{L}\) is stored as an adequate latent code. The latent code search process is summarized in Algorithm 2. Here, \(N_{iter}\) represents the number of iterations required to search for the latent code, which is set as 1,000.

figure b

In Algorithm 2, \(\epsilon\) is the discrepancy between the input and the output. Interpolation will be performed to obtain adequate latent codes. Slerp is performed in the latent dimension, as it has been widely accepted for Gaussian-sampled generative models owing to its accuracy [50]. The interpolated latent code is then sent to the decoder to generate the interpolated POD coefficient. The relevant procedure is summarized in Algorithm 3, where slerp denotes slerp. The interpolated flow field is then constructed by the combination of \(a_{i,p_{tgt}}\) and the pre-obtained POD modes, \(\phi _{i}\), as in Eq. (15):

$$\begin{aligned} \begin{aligned} q^{*}_{p_{tgt}}(x, t)={\bar{q}}(x)+\sum _{i=1}^{N_{m}} a_{i,p_{tgt}}(t) \phi _{i}(x) \end{aligned} \end{aligned}$$
(15)
figure c

The present pMOR procedure comprises two stages: offline and online. The offline stage includes FOM construction, POD, mNVAE training, and latent code searching. The offline stage must only be performed once. In contrast, the online stage is executed repeatedly for each parametric estimation. It includes latent code interpolation and the construction of the interpolated flow field. Because the online stage requires a relatively smaller amount of computational time, the POD-mNVAE pMOR scheme becomes efficient. Figure 4 illustrates a flowchart of the proposed methodology.

Fig. 4
figure 4

Flowchart for POD-mNVAE

Full size image

5 Numerical results

This section presents the application of the proposed POD-mNVAE for two FSI situations. First, it was applied to the flow field of a plunging airfoil. The plunging airfoil demonstrated the variation in the flow field with respect to the deformed grid. The results obtained by POD-mNVAE were compared with those of other POD-based ANNs in terms of accuracy and efficiency. Then, the POD-mNVAE is examined by the highly nonlinear FSI phenomenon, LCO. The LCO examines the applicability of the POD-mNVAE to various engineering problems with nonlinearity.

For both applications, Navier–Stokes CFD analysis was performed. CFD analysis and POD were performed using an AMD 3950X CPU at 4.11 GHz. The ANN model was constructed using Tensorflow 2.7.0 and the training was performed using an NVIDIA GeForce GTX 3090 GPU. The results obtained by the POD-mNVAE were evaluated by comparison with those obtained by FOM in terms of accuracy and computational time.

5.1 Plunging airfoil

5.1.1 Problem description

First, the prescribed plunging airfoil was analyzed. An airfoil with a chord length of 0.156 m was subjected to standard atmospheric inflow of 1 m/s. The airfoil plunges at a frequency of 10 rad/s while its amplitude varies. The plunging amplitude changes in ten variations, \(h=\left[ 0.05, 0.06, \cdots , 0.13, 0.14\right]\) m, as illustrated in Fig. 5. The flow field was discretized using 28,315 three-node triangular elements with 14,300 nodes. An open-source Navier–Stokes CFD solver, OpenFOAM v1912, was used to construct the snapshot.

Fig. 5
figure 5

Schematic of the plunging airfoil

Full size image

The snapshot matrix for various plunging amplitudes was obtained using the fully converged CFD results. 5s of FOM results with an interval of 0.01s were collected for the snapshot matrix. The total snapshot matrix \(W_{total}\) was then constructed by appending the snapshot matrices for each parameter in the row direction. After POD on \(W_{total}\) was completed, 100 POD modes were collected for the velocity, and one mode was collected for the grid deformation. The accumulated energy ratios of the POD modes are 99.9% and 99.9%, respectively. The first two POD mode shapes for the x-direction velocity u are shown in Fig. 6.

Fig. 6
figure 6

POD modes for the plunging airfoil, velocity component, u

Full size image

The current mNVAE for the plunging airfoil comprises six blocks in the encoder and decoder. The encoder comprises Conv1D blocks with \(\left[ 800, 400, 200, 100, 50\right]\) filters in a bottom-up network. The decoder comprises TransConv1D blocks with the same filters as in a top-down network. The latent dimensions for interpolation were set as 64. Detailed hyperparameters used for the present mNVAE training are summarized in Table 1.

Table 1 Hyperparameters for the present mNVAE training for the plunging airfoil
Full size table

After the training of mNVAE is completed, an adequate latent code for each parameter is sought. Then, slerp is performed, and the latent code for the target value, \(h=0.095\) m, is acquired. The interpolated POD coefficients were generated by the decoder, as shown in Fig. 7. Using Eq. (15), an interpolated flow field is created for the target parameter. The resultant interpolated and FOM flow fields are shown in Fig. 8.

Fig. 7
figure 7

Interpolated POD coefficient #1, velocity for the plunging airfoil

Full size image
Fig. 8
figure 8

Original and interpolated flow field around the plunging airfoil for \(h=0.095\) m at \(t=4.5\) s

Full size image

5.1.2 Accuracy and efficiency of POD-mNVAE

The accuracy of POD-mNAVE was evaluated with respect to the following seven categories:

  • \(\Delta V_{\text {avg}}\): Average velocity discrepancy.

  • \(\Delta f_{V,\text {avg}}\): Oscillation frequency discrepancy of the velocity component.

  • \(\Delta V_{pp}\): Peak-to-peak (oscillation amplitude) discrepancy of the velocity component.

  • \(\Delta V_{\text {point}}\): Velocity discrepancy at the 15 points of interest.

  • \(\Delta f_{x,\text {avg}}\): Oscillation frequency discrepancy of the grid deformation.

  • \(\Delta x_{pp}\): Peak-to-peak (oscillation amplitude) discrepancy of the grid deformation.

  • \(\Delta x_{\text {point}}\): Grid deformation discrepancy in the 15 points of interest.

Among the seven categories, the preceding four are discrepancies in the velocity components. The latter three are discrepancies in grid deformation. The 15 points of interest described in \(\Delta V_{point}\) and \(\Delta x_{point}\) were placed in the wake region. These points were placed where the changes in the physical variables were expected to be the largest. The locations of the 15 points are shown in the Appendix A, Fig. 16. The formulations for these seven categories are included in Appendix A. Table 2 summarizes the discrepancies in the plunging airfoil.

Table 2 Discrepancies between POD-mNVAE and FOM for the plunging airfoil
Full size table

In Table 2, the accuracy of the POD-mNVAE is determined to be significantly small, as most of them are less than 1\(\%\). The largest discrepancy was determined as 6.40\(\%\), which was \(\Delta V_{pp}\). A large discrepancy in \(\Delta V_{pp}\) was caused by the tendency to underestimate the oscillation amplitude. However, for the other categories, the discrepancies were smaller. In particular, for \(\Delta f_{x,avg}\), the discrepancy was determined as zero.

The computational procedure for POD-mNVAE comprises six steps. The time required for each computational step is summarized in Table 3. The entire interpolation process for POD-mNVAE consumes 82.7 h regarding the ten parameters. It can be divided into two components, 82.4 h for the offline stage and 0.29 h for the online stage. With the appropriate execution of the offline stage, the interpolation process is predicted to consume only 0.29 h. In conclusion, POD-mNVAE is capable of reducing 96.2\(\%\) of the computational time for each novel parametric estimation. POD-mNVAE will be efficient if repeated computations exceeding 12 times are required. The expected computational time in terms of the number of computations is as shown in Fig. 9.

Fig. 9
figure 9

Computational time in terms of the number of the computations for the plunging airfoil

Full size image
Table 3 Computational time result for the plunging airfoil
Full size table

5.1.3 Comparison against the other ANN methods

The proposed POD-mNVAE was then compared with other POD-based ANN methods. A comparison was performed between WGAN-GP [21], the previous version of mNVAE [51], and Gaussian process regression (GPR). The accuracy of various interpolation methods are summarized in Table 4. In this study, POD-mNVAE was found to be superior. The discrepancy in the current POD-mNVAE is the smallest, except for \(\Delta V_{avg}\), \(\Delta V_{PP}\), and \(\Delta x_{PP}\). For these categories, the WGAN-GP [21] and GPR performed better. However, the current POD-mNVAE was the most accurate overall. Improved accuracy for the current mNVAE was observed because of the hybrid weighted mean squared error-Kullback–Leibler divergence (MSE-KLD) loss function. The current loss function was empirically determined to significantly enhance accuracy when used for a continuous dataset. The computational time required was obtained as the sum of the times required for Algorithms 1, 2, and 3. Notably, the proposed method was significantly efficient compared to other ANN methods. The current mNVAE required 6.37 h whereas the previous version of mNVAE needed 17.82 h, and WGAN-GP used 77.33 h for training. However, it is noteworthy that GPR was the most efficient as it took less than 0.1 h. The current mNVAE reduced the training time by more than 74 % compared with the previous version of the mNVAE [51]. It is also capable of reducing the training time by more than 91 % compared with WGAN-GP [21]. The current mNVAE was the most efficient, as it trains 20 POD coefficients per network. In contrast, the previous version of mNVAE trained a single POD coefficient per network, and WGAN-GP trained 10 POD coefficients per network. Training more POD coefficients per network leads to a smaller number of networks required for interpolation. The current mNVAE trains more POD coefficients per network with accuracy because the modified loss function enables a further compactly constructed latent space. However, the training speed of the WGAN-GP was slow owing to the inherent instability. To ensure stable training, a gradient penalty was adopted for the generator (similar to the decoder for the GAN). For the same reason, the critic network (similar to the encoder) was trained for five iterations per epoch [21]. In general, the current mNVAE is the most efficient yet accurate among the previously introduced unsupervised learning methods.

Table 4 Accuracy of interpolation models for the plunging airfoil
Full size table

5.2 Limit cycle oscillation (LCO)

5.2.1 Problem description

The LCO of an aircraft is a periodic, nondiverging oscillation that may lead to structural fatigue and failure. It is an FSI phenomenon caused by either or both nonlinearities in the fluid and structural dynamics. An accurate LCO analysis is typically performed using a high-fidelity nonlinear FSI analysis. Generally, for fluid analysis, either Euler or Navier–Stokes CFD, is implemented owing to the high nonlinearity. Consequently, LCO analysis is challenging and tedious. Because the LCO amplitude and frequency differ by flight speed, iterative computation is required to determine the safe flight speed limit of an aircraft. In this section, the POD-mNVAE is examined for a realistic engineering problem with nonlinearity.

The analysis used in this section was derived from O’Neil et al. [52]. An airfoil with a chord length of 0.2128 m was subjected to standard atmospheric conditions as in Fig. 10. The inflow speed ranged from 20 to 45 m/s at 5 m/s intervals. The airfoil had two DOFs: pitch and heave. Both the pitch and heave stiffnesses are nonlinear in their cubic terms. The equations for the pitch and heave stiffnesses are expressed in Eq. 16 as follows:

$$\begin{aligned} \begin{aligned} K_{\alpha } = 2.57(\alpha +500\alpha ^3)\\ K_{h} = 0.09(h+2860h^3)) \end{aligned} \end{aligned}$$
(16)

The parameter to be interpolated for the current analysis was flight speed. The flight speed of the airfoil will change in six variations, \(U=\left[ 20, 25, 30, 35, 40, 45\right]\)m/s, as shown in Fig. 14. The relevant flow field was discretized using 19,543 quadrilateral elements comprising 19,381 nodes. For CFD, the Navier–Stokes solver ANSYS was employed. To model the structural nonlinearity, a user-defined function was used. The preliminary LCO analysis exhibited a good correlation with the wind tunnel test [52]. The LCO onset speed was determined as 16 m/s for ANSYS FSI, whereas it was “slightly higher than 15 m/s” for the wind tunnel test [52].

Fig. 10
figure 10

Schematic of the airfoil under LCO

Full size image

The snapshot matrix for various flight speeds was obtained from the fully converged CFD result. 2s FOM results with an interval of 0.01s were collected for the snapshot matrix. The total snapshot matrix \(W_{total}\) was then constructed by appending the snapshot matrices for each parameter in the row direction. After POD on \(W_{total}\) was completed, 40 POD modes were collected for the velocity, and two modes were collected for the grid deformation. The first POD modes for velocity and grid deformation are shown in Fig. 11. The accumulated energy ratio for both POD modes was determined as 99.9

Fig. 11
figure 11

POD modes for LCO analysis

Full size image

The current-interpolating mNVAE comprises eight blocks in the encoder and decoder. The encoder comprises Conv1D blocks with \(\left[ 800, 400, 200, 100, 50, 20, 10\right]\) filters in a bottom-up network. The decoder comprises TransConv1D blocks with the same filters as in a top-down network. The latent dimension for the interpolation was set as 256 to accommodate intricate pattern recognition. Detailed hyperparameters used for mNVAE training are summarized in Table 5. After the training of mNVAE was completed, an adequate latent code for each parameter was sought. Then, slerp was performed, and the latent code for the target value, \(U=32.5\)m/s, was acquired. The interpolated POD coefficients were generated by the decoder, as shown in Fig. 12. Using Eq. (15), the interpolated flow field was generated for \(U=32.5\)m/s. The resultant airfoil movement of the interpolated flow field and FOM is illustrated in Fig. 13. The fully interpolated flow field is illustrated in Fig. 14.

Table 5 Hyperparameters for mNVAE training for LCO analysis
Full size table
Fig. 12
figure 12

Interpolated POD coefficient #1, dx, of LCO analysis

Full size image
Fig. 13
figure 13

Original and interpolated movement of the airfoil undergoing LCO

Full size image
Fig. 14
figure 14

Original and interpolated flow field around the airfoil undergoing LCO

Full size image

5.2.2 Accuracy and efficiency of POD-mNVAE

The accuracy of the POD-mNVAE was evaluated using the seven categories mentioned in the plunging airfoil. Fifteen points of interest were placed behind the airfoil, where the changes in the physical variables were expected to be the largest. The 15 locations are shown in Appendix A, Fig. 16. Table 6 summarizes the discrepancies in the POD-mNVAE for LCO analysis.

Table 6 Discrepancies between POD-mNVAE and FOM for LCO analysis
Full size table

In Table 6, the accuracy of the POD-mNVAE was significantly small. The discrepancy in the velocity component was 3.21%. The other categories displayed similar discrepancies, except for frequency, which was as small as 0.73%. The discrepancies in grid deformation were smaller, ranging from 0% to 0.32%.

The computational procedure for POD-mNVAE comprises six steps. The time required for each computational step is summarized in Table 7. The entire interpolation process using POD-mNVAE consumes 284.4 h for the six parameters. It may be divided into two components, 283.8 h for the offline stage and 0.59 h for the online stage. With the appropriate execution of the offline stage, the interpolation process is predicted to consume only 0.59 h. In conclusion, the proposed POD-mNVAE is capable of reducing by 98.7\(\%\) of the computational time for each novel parametric estimation. The proposed POD-mNVAE is efficient if the number of repeated computations exceeds seven. The expected computational time in terms of the number of computations is shown in Fig. 15.

Fig. 15
figure 15

Computational time in terms of the number of computations for LCO analysis

Full size image
Table 7 Computational time result for LCO analysis
Full size table

6 Conclusions

In this study, an improved data-driven pMOR scheme was proposed to construct an accurate ROM. The present methodology, referred to as POD-mNVAE, combines an interpolating neural network, mNVAE, and POD. POD is used to reduce the number of DOFs in the FOM result, whereas mNVAE is used to compress the temporal information inherent in the POD output, that is, the POD coefficient. The POD-mNVAE was capable of accurately constructing the ROM while significantly improving the computational time.

The POD-mNVAE was applied to two FSI situations: the flow field surrounding a prescribed plunging airfoil and LCO. The evaluation was performed with regard to accuracy and computational time. The present POD-mNVAE produced accurate results. The plunging airfoil exhibited a discrepancy of less than 1\(\%\) and that of LCO was approximately 3\(\%\). The proposed POD-mNVAE achieves a reduction in computational time of 96\(\%\) for the plunging airfoil and 98\(\%\) for LCO at the cost of the pre-executed offline stage. Furthermore, the current mNVAE was compared with the previous versions of mNVAE, WGAN-GP, and GPR to assess its superiority. The current mNVAE produced the most accurate results. The present methodology is applicable to other fields, such as structural dynamics. In particular, the present approach was used to construct the ROM of a highly nonlinear FSI.

However, it has shortcomings. The present method may not be used for problems in which different parameters will exhibit different dynamics. Rapid change in physical dynamics will lead to incapability of using POD modes universally across the parameters. To overcome such limitation, adopting the local or on-the-fly MOR methods may be considered as in [53, 54]. The present method generally cannot extrapolate beyond the prescribed parametric space. It is due to the universal use of POD modes that are constrained within the parametric space. Regarding the accuracy of the present method, sufficient number of sampling need to be conducted. Empirically, more than 5 sampling will be desirable. mNVAE requires more than 5 data points to recognize nonlinear pattern accurately. Also, those sampling should be conducted so that the change in physical dynamics may be captured in POD modes. Finally, the present method cannot extrapolate beyond FOM computation duration. Simple modification such as inserting LSTM network will be considered to enable such temporal extrapolation.

In the future, the current POD-mNVAE will be evaluated for an extremely large three-dimensional (3D) full FSI situation. It will be investigated for a full CFD–CSD combination for large structures, such as a full 3D passenger jet aircraft analysis in maneuver. For large three-dimensional FSI problems, the present framework will be used as it is. However, MOR stage is expected to be a challenge since POD will require extensive memory and computational time. To mitigate such limitation, other dimensionality reduction methods such as the local POD and autoencoder will be investigated.