Evolution of the bi-stable wake of a square-back automotive shape

Abstract

Square-back shapes are popular in the automotive market for their high level of practicality. These geometries, however, are usually characterised by high drag and their wake dynamics present aspects, such as the coexistence of a long-time bi-stable behaviour and short-time global fluctuating modes that are not fully understood. In the present paper, the unsteady behaviour of the wake of a generic square-back car geometry is characterised with an emphasis on identifying the causal relationship between the different dynamic modes in the wake. The study is experimental, consisting of balance, pressure, and stereoscopic PIV measurements. Applying wavelet and cross-wavelet transforms to the balance data, a quasi-steady correlation is demonstrated between the forces and bi-stable modes. This is investigated by applying proper orthogonal decomposition to the pressure and velocity data sets and a new structure is proposed for each bi-stable state, consisting of a hairpin vortex that originates from one of the two model’s vertical trailing edges and bends towards the opposite side as it merges into a single streamwise vortex downstream. The wake pumping motion is also identified and for the first time linked with the motion of the bi-stable vortical structure in the streamwise direction, resulting in out-of-phase pressure variations between the two vertical halves of the model base. A phase-averaged low-order model is also proposed that provides a comprehensive description of the mechanisms of the switch between the bi-stable states. It is demonstrated that, during the switch, the wake becomes laterally symmetric and, at this point, the level of interaction between the recirculating structures and the base reaches a minimum, yielding, for this geometry, a $7\%$ reduction of the base drag compared to the time-averaged result.

1 Introduction

The need to reduce aerodynamic drag is becoming increasingly important in the modern automotive industry, as it represents the main source of losses for any road vehicle travelling at speeds greater than about 80 kph. Its importance is expected to increase further as battery powered electric vehicles become more common and manufacturers strive to get the maximum range from the limited amount of energy available in their batteries. Whatever other range extending technologies are deployed (for example, stop start, regenerative braking, etc.), minimising the losses is the most effective way to achieve an acceptable range for the customers.

Square-back vehicles are a popular choice with customers thanks to their large cabin space and easy access. The large base area, however, can yield a high level of aerodynamic drag compared to more streamlined rear-end shapes such as optimised fast-back or notch-back cars. The steady-state topology of the wake of square-back geometries has been well characterised; for example, CFD simulations performed by Krajnovic and Davidson (2003) and Roumeas et al. (2009) show that it consists of a toroidal structure that interacts with the surrounding shear layers to form a pair of counter-rotating vortices downstream of the near wake. The existence of these structures has been confirmed experimentally by Perry et al. (2016a).

The characterisation of the dynamics of such wakes, fundamental for the implementation of new drag reduction methods, is still the object of intense research activity and debate among the researchers.

Duell and George (1999) using a square-back model based on the work of Ahmed et al. (1984) with a base aspect ratio (${\rm{{AR}}} = W/H$) of one observed the existence of a periodic pumping mode of the wake caused by the interaction between the upper and lower parts of the ring vortex. This mode was shown to trigger periodic fluctuations of the base pressure, with a characteristic Strouhal number of ${{\rm{{St}}}_{\rm{{H}}} = 0.069}$ (${{\rm{{St}}}_{\rm{{H}}}}$ based on the model height H). Its suppression, achieved by adding a rear cavity, resulted in an increase in the mean base pressure of up to $11 \%$, accompanied by a noticeable reduction of the pressure fluctuations. Similar results were obtained by Khalighi et al. (2001) in experimental and numerical investigations using a different square-back geometry with an aspect ratio of 1.4.

Most recently, Grandemange et al. (2012a) reported the existence of a permanent reflectional symmetry breaking state for the wake of a $26 \, {\rm{{mm}}}$ high Ahmed body tested in a low-speed hydrodynamic facility. A first bifurcation from the trivial symmetric state to a steady reflectional symmetry breaking state was observed at a model height-based Reynolds number ${\rm {Re}}_{\rm {H}}$ of 340. The reflectional symmetry breaking state then becomes unsteady after a second bifurcation at ${\rm {Re}}_{\rm {H}} = 410$, resulting in a bi-stable behaviour that has subsequently been demonstrated at Reynolds numbers of up to $10^7$ (Grandemange et al. 2015). The same trend has been captured in the large eddy simulations performed by Evstafyeva et al. (2017).

Grandemange et al. (2013b) further characterised this bi-stable behaviour by testing an Ahmed body in a 3/4 open jet wind tunnel at ${\rm {Re}}_{\rm {H}} = 9.2 \times 10^4$. In these conditions, it was found that the characteristic time between switches can be estimated as $T_l \sim {10^3} H/V_{\infty }$, where $V_{\infty }$ is the free-stream velocity. The succession of reflectional symmetry breaking states was initially thought to behave like a stationary Markov chain, although more recent findings from Varon et al. (2017) suggest that the low-frequency dynamics may be considered as a weak chaotic process with two attractors. In Grandemange et al. (2013b), it is also shown that this long period motion yields an unsteady side force that was inferred to be responsible for part of the drag. A shorter time-scale $T_s \sim 5 H/V_{\infty }$ was also observed and was attributed to weak coherent oscillations of the wake in the vertical and lateral directions, associated with the interaction of top–bottom and lateral shear layers, but no evidence of the pumping motion was found. In contrast, evidence of the existence of the pumping mode was found by Volpe et al. (2015) using the same geometry at higher Reynolds numbers (${\rm {Re}}_{\rm {H}} = 5.1 \times 10^5$ and ${\rm {Re}}_{\rm {H}} = 7.7 \times 10^5$), together with the bi-stable behaviour and the other two short-time-scale modes. In particular, the wake pumping, with a normalised frequency of ${\rm {St}}_{\rm {H}} = 0.08$, was found to be predominant in the shear layer of the recirculation bubble, whilst the other two modes, with ${\rm {St}}_{\rm {H}} = 0.13$ and ${\rm {St}}_{\rm {H}} = 0.19$, were found to be more visible downstream of the wake closure.

Focusing on the effects of base aspect ratio on the bi-stable mode Grandemange et al. (2013a) showed a bi-stable motion of the wake in the lateral direction for $W>H$ and in the vertical direction when $H>W$, suggesting the existence of a link between this phenomenon and the multi-stable behaviour already seen for axisymmetric bodies such as spheres (Chrust et al. 2013, Grandemange et al. 2014a) and cylinders with a sharp trailing edge (Rigas et al. 2014, Gentile et al. 2016). In the axisymmetric cases, the instantaneous wake has been shown to explore all azimuthal locations $\theta _{\rm{{W}}}$ uniformly, because of the infinite number of azimuthal symmetry planes. Grandemange et al. (2012b), considering an axisymmetric body, also showed that, even when the wake is forced to be symmetric in the lateral direction ($\theta _{\rm{{W}}} = \pi /2$), an asymmetry along the vertical direction can still be seen in the time-averaged field. Furthermore, the number of preferred positions of the wake can be reduced to just two when a perturbation with an azimuthal wave number of $m = 2$ is applied to either a sphere (Grandemange et al. 2014a) or a cylinder (Grandemange et al. 2012b) resulting in a bi-stable behaviour.

The need to reduce the drag generated by bluff bodies has led over the past few decades to the development of flow control strategies, focusing mainly on the alteration or suppression of the vortex shedding (Choi et al. 2008). Most recently researchers have focused their attention on the suppression of the wake bi-stability as a way to achieve the same goal. Grandemange et al. (2014b) demonstrated a base drag reduction of between 4% and $9\%$ for an Ahmed body when the lateral symmetry of the wake was restored by means of a vertical control cylinder positioned in the core of the wake’s reverse flow. This suggested the existence of an unstable branch for the solution of the equations that describe the wake dynamics, dubbed the reflectional symmetry preserving mode by Cadot et al. (2015).

Applying a cavity to the base, Evrard et al. (2016) found that the strength of the vortex system associated with the reflectional symmetry breaking mode decreased as the cavity depth was increased, yielding a reduction of the drag until a saturation was reached for a depth $d> 0.24 H$. The stabilising effect of the cavity was modelled using a Langevin equation. Furthermore, a new topology was proposed for each reflectional symmetry breaking state, consisting of a horseshoe vortical structure. According to this model, the toroidal vortex usually reported in the literature (Krajnovic and Davidson 2003; Roumeas et al. 2009) is the result of the temporal average of these asymmetric structures. No information, however, was provided on the effects produced on the pumping mode by the application of the cavity.

A feedback control system aiming to symmetrise the bimodal dynamics of a blunt body’s turbulent wake was proposed by Li et al. (2016). The flow was controlled by means of two lateral slit jets and monitored with pressure sensors mounted on the rear surface. A $2 \%$ increase of the base pressure was achieved by stabilising the unstable symmetric mode observed during the transition between bi-stable states. A similar result was achieved by Brackston et al. (2016), employing a more efficient actuating system with moving flaps. In this case, the feedback control loop was designed using a modelling approach similar to that suggested by Rigas et al. (2015), based on a nonlinear Langevin equation consisting of a deterministic part, describing the evolution of the large-scale structures, and a stochastic term, capturing the effects of the turbulent forcing.

A different way to control the wake bi-stability was found by Perry et al. (2016b) looking at the effects of high aspect ratio tapers applied to the top and bottom trailing edges of a Windsor body. It was seen that the tendency of the wake to develop this particular instability tends to decrease as the distance between the top and bottom shear layers is reduced by the upwash or downwash induced by the small slants. A drag reduction over the square-back case, however, was obtained only when the weakening of the bi-stable mode was accompanied with the re-symmetrisation of the time-averaged wake topology in the vertical direction.

In the present work, the bi-stable behaviour described in Perry et al. (2016b) for the Windsor body is further investigated with the aim of providing an answer to the following questions: is there any relationship between the short- and long-time unsteady motions of the wake? How does the switch between the two bi-stable states occur? Does the switch have any quantifiable effect on the aerodynamic forces? For this reason, two yaw angles, corresponding respectively to a bi-stable case ($\psi = 0^\circ$) and a stable asymmetric case ($\psi = + \, 0.6^\circ$), are considered. The effect of the bi-stable mode on the aerodynamic drag is assessed for the first time by applying wavelet transform to balance data. Finally, the existence of a symmetric mode (reflectional symmetry preserving mode according to Cadot et al. (2015)) during the transition between two laterally asymmetric states is proven.

2 Experimental methodology

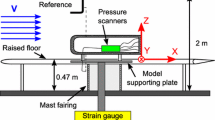
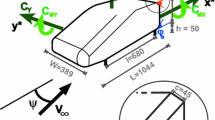
The Windsor body The experimental programme employed the Windsor body used in the work from Perry et al. (2016b), because the slanted front-end generates a flow field more representative of real cars than the widely used Ahmed body (Ahmed et al. 1984). At the scale used here, the model is approximately equivalent to a 1/4 scale passenger car and results in a tunnel blockage of $4.4\%$. For all tests, the ground clearance was set at $50 \, {\rm{{mm}}}$ ($17.3\%$ of the model height), with a tolerance of $0.2^{\circ }$ for the pitch angle.

Fig. 1

a Schematic representation of the Windsor body; b representation of the model base with pressure tappings (the base is located at $x^*=1.81$ from the origin of the reference system) and the 2D-3C PIV planes considered in the present work (placed at $x^*=2.31$ and $x^*=3.31$). The red square on the model base sketched in b denotes the area associated with the $n{\rm{{th}}}$ tap used for the estimation of the area-weighted drag. All the dimensions reported in a in are expressed in millimeters. For the reference system, see SAE (2010)

The model was mounted via four pins (M8 threaded bar) to the six-component balance located beneath the working section. The pins were in locations representative of the front and rear axles and $10 \, {\rm{{mm}}}$ inboard of the model sides. The SAE coordinate system (SAE 2010) is used throughout; the X axis is aligned with the flow in the streamwise direction, the Z axis is vertical, positive upwards, and the Y axis follows a right handed coordinate system. The origin is on the ground plane at mid wheelbase, mid track (Fig. 1a).

All the quantities presented throughout the paper have been normalised using the model height H as the reference length and the value of the free-stream velocity $V_\infty$ and are denoted with the superscript “$*$”. For the sake of clarity, all the time-averaged quantities are indicated with the superscript “$-$” whilst the superscript “$\sim$” is used to denote quantities extracted from conditionally averaged fields.

The wind tunnel. All experiments were carried out in the Loughborough University Large Wind Tunnel. This test facility, described in Johl (2010), has a working section measuring $1.92 \times 1.32 \times 3.6 \, {\rm{{m}}} \, (W_{\rm{{T}}} \times H_{\rm{{T}}} \times L_{\rm{{T}}})$ and is equipped with a fixed floor without any upstream boundary layer treatment. In empty conditions, the free-stream turbulence level in the test section is approximately $0.2\%$, with a flow uniformity of $\pm \, 0.4\%$ of the mean flow value. In this state, the boundary layer thickness at the model origin was measured to be $\delta _{99} = 64 \, {\rm{{mm}}}$. All tests were performed with a free-stream velocity $V_{\infty }$ of $40 \, {\rm{{m}}}/{\rm{{s}}}$, corresponding to a Reynolds number ${\rm {Re}}_{\rm {H}}$ of $7.7 \times 10^{5}$ based on the model height H.

Balance measurements. The aerodynamic loads were recorded by means of a six-component virtual centre balance, located under the working section of the tunnel. It features analogue-to-digital conversion at the load cell to minimise signal degradation, and an automated yaw mechanism with a positional accuracy of $\pm \, 0.1^\circ$. Further information can be found in Johl (2010). The aerodynamic loads were sampled at $100 \, {\rm{{Hz}}}$ for $t = 630 \, {\rm{{s}}}$ (corresponding to $8720 \times 10^4$ convective units $t^{*}$, with $t^{*} = t \times V_{\infty }/H$). Before starting to log the data, a $30 \, {\rm{{s}}}$ ($t^{*} = 4.152 \times 10^3$) settling time was used for all measurements. The recorded values of the forces have been normalised using the following equation:

$$\begin{aligned} C_{\rm{{Fi}}} = \frac{\rm{{Force}}}{0.5 \rho S_{\rm{{M}}} V_\infty ^2}, \end{aligned}$$

(1)

where $\rho$ is the air density and $S_{\rm{{M}}}$ is the projected model frontal area ($S_{\rm{{M}}}=0.1124 \, {\rm{{m}}}^2$). The coefficients were corrected for blockage effects using Eq. (2):

$$\begin{aligned} C_{{\rm {Fi}}_{\rm {Cor}}} = {C_{\rm {{Fi}}}}(1-B)^2, \end{aligned}$$

(2)

where B denotes the blockage value, given by the ratio between the model frontal area $S_{\rm{{M}}}$ and the tunnel working section cross-sectional area $S_{\rm{{T}}}$. The coefficients are accurate within $\pm \, 2$ counts (Johl 2010).

The effect of the bi-stable mode on the three components of the aerodynamic force was studied by means of wavelet analysis, using the Matlab^® toolbox developed by Grinsted et al. (2004). This technique allows the frequency content of a discrete time-series f(t) to be determined whilst assessing its variation in time. In addition, by calculating the cross-wavelet transform for two time-series referring to different components of the aerodynamic force, regions in the time–frequency domain where the two series have a high common power can be identified.

Pressure measurements. The pressure on the model base was recorded by populating the rear facing surface with a grid of pressure taps connected via urethane tubes (with a length of $550 \, {\rm{{mm}}}$) to a 64 channel miniature pressure scanner (with a manufacturer quoted accuracy of $\pm \, 1.47 \, {\rm{{Pa}}}$) mounted inside the model. A total of 45 taps were used. The taps were placed with a finer distribution close to the model edges, to get a more accurate representation of the pressure distribution in the regions with the highest gradients (see Fig. 1b). Pressure data were recorded at $260 \, {\rm{{Hz}}}$ for $630 \, {\rm{{s}}}$ ($t^{*} = 8720 \times 10^4$). The free-stream dynamic and static pressures were acquired $1870 \, {\rm{{mm}}}$ upstream of the model, at the start of the working section. The pressure signals were corrected for magnitude and phase distortions caused by the tubing by applying the correction proposed by Sims-Williams and Dominy (1998). Once the pressure coefficients were calculated, Eq. (3), the results were corrected for blockage using the MIRA correction (based on continuity): Eq. (4):

$$\begin{aligned} C_{\rm{{P}}}= & {} \frac{p - p_\infty }{0.5 \rho S_{\rm{{M}}} V_\infty ^2} \end{aligned}$$

(3)

$$1 - C_{{\rm{P}}_{\rm {corr}}}= \left( 1-C_{\rm{{p}}} \right) \left( 1-B \right) ^2,$$

(4)

where $p_\infty$ is the free-stream static pressure. The base drag was then estimated by integrating the measured pressure field:

$$\bar{C}_{{{\text{D}}_{{{\text{Rear}}}} }} = - \frac{1}{S}\int {\int_{S} {\bar{C}_{{\text{p}}} } } \times {\text{d}}S \simeq - \frac{1}{S}\sum\limits_{{i = 1}}^{{N_{{{\text{tap}}}} }} {\bar{C}_{{{\text{p}}_{{\text{i}}} }} S_{{\text{i}}} } ,$$

(5)

where $\overline{C}_{{\rm{p}}_{\rm {i}}}$ is the time-averaged value of the pressure coefficient recorded by the $n{\rm{{th}}}$ tap and $S_{\rm{{i}}}$ is the associated area (see Fig. 1b).

Since the flow field analysed in the present study is highly sensitive to any asymmetry present in the experimental setup, the model was yawed to the onset flow until the most symmetric base pressure distribution was achieved, following a similar procedure to that adopted by Evrard et al. (2016). The resulting value of yaw angle was assumed to be where the model axis and onset flow axis were aligned.

The main features of the unsteady pressure field were extracted by means of proper orthogonal decomposition (POD). First introduced into turbulence research by Lumley (1967), this method allows for the decomposition of a generic unsteady field into a set of orthogonal modes that are ranked by their energy content. The first few modes are representative of the most dominant coherent unsteady structures and can be used to build a reduced order model describing the main dynamic features of the field.

PIV measurements. Stereoscopic particle image velocimetry (PIV) measurements were performed on planes orthogonal to the onset flow, at two streamwise locations, $x^{*} = 2.31$ and $x^{*} = 3.31$ (see Fig. 1b). These locations were chosen, since they correspond approximately to 1/3 of the bubble length and the end of the recirculating region. Two LaVision^® CMOS cameras with a resolution of $2560 \times 2160$ pixels and a pixel size of $6.5 \times 6.5 \, {\upmu {\rm {m}}}^2$ were employed, together with a Litron^® $200 \, {\rm{{mJ}}}$ double pulsed Nd:YAG laser and PIVTec 45 atomiser, generating $1 \, {\upmu {\rm {m}}}$ droplets of DEHS. The cameras were mounted on a pair of aluminium rails placed inside the tunnel working section, following the arrangement already used by Wood (2015). The separation angle between the cameras was $\approx 50^{\circ }$. Each camera was equipped with a Nikon^® lens, with a focal length of $50 \, {\rm{{mm}}}$, mounted on a tilt system to satisfy the Scheimplfug criterion (Prasad 2000). The aperture was set at $f_{\#} = 4$. The resultant field of view ($W_{\rm{{f}}} \times H_{\rm{{f}}}$) was $520 \times 400 \, {\rm{{mm}}}$.

During each acquisition, 2000 statistically independent image pairs were captured at a sampling frequency of $15.00 \, {\rm{{Hz}}}$ to match the sampling time used by Perry et al. (2016b) ($133.3 {\rm{{s}}}$ or $t^{*} = 1845 \times 10^4$). The data  was then processed using DaVis 8.2.0. Image pre-processing was applied to the recordings to mitigate the effects of image distortion, background light intensity, as well as spurious reflections. A calibration correction based on a pinhole model was applied; background subtraction was performed and the outmost regions of the field of view were discarded using a geometric mask. The size of the field of view was therefore reduced to $430 \times 340 \, {\rm{{mm}}}$. A multi-pass scheme for cross-correlation was applied (Willert and Gharib 1991), starting with an interrogation window with a size of $64 \times 64$ pixels and a $50\%$ overlap between cells and ending with windows of $32 \times 32 \, {\rm{{mm}}}$ pixels and a $75\%$ overlap. This resulted in a spatial resolution of $2.8 \times 10^{-6} \, {\rm{{m}}}^2$. The level of uncertainty associated with the measurements was estimated to be 0.5% and $1.5 \%$ of the mean and RMS values of the free-stream velocity, having considered a $99 \%$ confidence level (Benedict and Gould 1996).

The unsteady features of the velocity field were also analysed by applying POD to the resulting vector fields, but in this case, the snapshot method developed by Sirovich (1987) was employed, due to its higher computational efficiency with this data, where the temporal domain is much smaller than the spatial domain.

Throughout the paper, $u^{*}$, $v^{*}$, and $w^{*}$ are used to indicate the normalised component components of the velocity along $x^{*}$, $y^{*}$, and $z^{*}$.

3 Results and discussion

3.1 Time-averaged wake topology

The time-averaged base pressure distributions are presented in Fig. 2a, b for the two yaw angles considered in the present work ($\psi = 0^{\circ }$ and $\psi = + \, 0.6^{\circ }$). In both cases, the results are in good agreement with those published in Pavia et al. (2016) and Perry et al. (2016b) apart from a small difference in the location of the rear stagnation point for $\psi = 0^{\circ }$. This arises, because the time-averaged wake topology in the vertical direction is the result of the delicate equilibrium between the top and bottom shear layers (Barros et al. 2017) and is, therefore, very sensitive to pitch. Such element can, indeed, have a noticeable effect on the long-time wake dynamics, as pointed out by Gentile et al. (2017) in the case of an axisymmetric body with a flat base. To ensure repeatability, all tests reported in this paper were set with an accuracy of $\pm \, 0.2^{\circ }$ on pitch. Figure 2a shows the static pressure to be relatively constant, without any strong pressure gradient in either the horizontal or vertical direction. A similar uniformity can be seen in the PIV cross-planes taken at $x^{*}= 2.31$ and $x^{*}= 3.31$. On the first plane ($x^{*}= 2.31$, Fig. 2c), the wake shows a degree of asymmetry in the lateral direction, probably due to the slight predominance of one of the two bi-stable states. This asymmetry is highlighted by the presence of a source along the horizontal plane of symmetry and close to the left-hand side of the model. Once the streamlines reach the edge of the base, they converge into four sinks, located at each corner, defining the four shear layers. Downstream ($x^{*}= 3.31$, Fig. 2e), as the wake closes, the source is replaced with a pair of sinks, aligned in the horizontal direction, to which the streamlines running from each side of the flow field converge, leading to the formation of a pair of counter-rotating vortices.

When the model is yawed by $0.6^{\circ }$, these two vortices are rotated by $90^{\circ }$ (Fig. 2f) and moved towards the windward side of the base and two vertically aligned recirculating structures become evident on the opposite side of the base for $x^{*}= 2.31$ (Fig. 2d). In combination, these elements suggest a single hairpin vortex that starts on the leeward side of the model close to the base and then moves towards the windward side while approaching the wake closure. As a consequence, the base pressure distribution loses its uniformity and a strong gradient appears in the horizontal direction. This contributes to an increase in the side force, which varies from $\overline{C}_{\rm{{Y}}} = 0.002$ at $\psi = 0.0^{\circ }$ to $\overline{C}_{\rm{{Y}}} = 0.052$ at $\psi = + \, 0.6^{\circ }$. This is accompanied with a drag increase (from $\overline{C}_{\rm{{D}}} = 0.273$ at $\psi = 0.0^{\circ }$ to $\overline{C}_{\rm{{D}}} = 0.279$ at $\psi = + \, 0.6^{\circ }$) and a small change in the magnitude of the vertical force (from $\overline{C}_{\rm{{L}}} = - \, 0.030$ at $\psi = 0.0^{\circ }$ to $\overline{C}_{\rm{{L}}} = - \, 0.033$ at $\psi = + \, 0.6^{\circ }$). More noticeable is the change of the lift distribution between the two axles, which varies from $\overline{C}_{{\rm{L}}_{\rm {f}}} = - \, 0.013 \, , \, \overline{C}_{{\rm{L}}_{\rm {r}}} = - \, 0.017$ for $\psi = 0.0^{\circ }$ to $\overline{C}_{{\rm{L}}_{\rm {f}}} = - \, 0.002 \, , \, \overline{C}_{{\rm{L}}_{\rm {r}}} = - \, 0.031$ for $\psi = + \, 0.6^{\circ }$, arguably due to an alteration of the A pillar vortices.

Additional unsteady information is seen from the root mean square of the pressure fluctuation. For $\psi = 0.0^{\circ }$, a region with a high level of unsteadiness develops at the centre of each of the two vertical halves of the base (Fig. 2g). This unsteadiness is associated with the switching of the rear stagnation point and also reported in the literature for bi-stable wakes [see Volpe et al. (2015)]. As the model is yawed away from the most symmetric position (Fig. 2h), the wake “locks” into a single state, leading to the disappearance of the bi-lobe distribution and a noticeable reduction in the level of unsteadiness, confirming the results of the similar experiment performed by Pavia et al. (2016).

Fig. 2

a and b time-averaged base pressure distributions; c and d time-averaged velocity fields at $x^{*} = 2.31$ from the origin of the reference frame defined in Fig. 1a; e and f time-averaged velocity fields at $x^{*} = 3.31$ from the origin of the reference frame defined in Fig. 1a; g and h root mean square of the pressure fluctuation ($\Delta C_{\rm{{p}}}$) over the model base. Data recorded for $\psi = 0.0^{\circ }$ (left-hand side column) and $\psi = + \, 0.6^{\circ }$ (right-hand side column). The streamlines in c–f are drawn considering the in-plane components of the velocity field

Fig. 3

a Continuous wavelet transform (CWT) of the three components of the aerodynamic force for $\psi = 0.0^{\circ }$; b cross-wavelet transform (XWT) between $C_{\rm{{L}}}$ and $C_{\rm{{D}}}$, $C_{\rm{{Y}}}$ and $C_{\rm{{D}}}$, and $C_{\rm{{Y}}}$ and $C_{\rm{{L}}}$ for $\psi = 0.0^{\circ }$. For the sake of simplicity, only the lower portion of the frequency domain has been reported in b. The colour scale is proportional to the wavelet power spectrum and is represented in octaves. The shaded region defines the cone of influence (COI) where the edge effects that may distort the results become predominant. The arrows superimposed on the colour maps presented in b show the local phase difference between the two signals of each cross-correlation; arrow pointing right: signals in phase; left: signals in phase opposition; down: first signal leading the second signal by $90^{\circ }$. For further information, see Grinsted et al. (2004)

3.2 Effects of the bi-stable mode on the aerodynamic forces

Although several authors have already measured how bi-stability affects the aerodynamic side force (Grandemange et al. 2015) and the related moments (Perry et al. 2016b), its effect on the other components of the aerodynamic force have only been speculated (Grandemange et al. 2013b) or inferred by perturbing the wake using external means (Grandemange et al. 2014b). In the present work, these effects were investigated directly by applying wavelet analysis to the unsteady data set logged from the balance. The results are presented in Fig. 3a.

At very low frequency (${{\rm{St}}_{\rm {H}}} \le 7.1 \times 10^{-4}$), there is a strong correlation in the side force for $\psi = 0.0^{\circ }$. A much lower level of correlation exists at this frequency for $C_{\rm{{D}}}$ and $C_{\rm{{L}}}$, confirming that the bi-stability is mainly affecting the lateral component of the aerodynamic force. Note that in all cases, the energy bands centred around ${{\rm{St}}_{\rm {H}}} \simeq 4.5 \times 10^{-2}$ are the resonant frequencies of the balance (Baden Fuller 2012).

Applying the cross-wavelet transform to the same signals, Fig. 3b, (for simplicity focusing only on the lower portion of the frequency spectrum), the phase angle, represented by the direction of the arrows superimposed on the colour maps, tends to remain constant in the regions characterised by the highest levels of correlation, confirming the existence a causal relationship between the two correlated signals in that specific portion of the time-frequency domain. In particular, $C_{\rm{{Y}}}$ and $C_{\rm{{D}}}$ appear to be in phase in the high-energy region located around ${{\rm{St}}_{\rm {H}}} \simeq 1.8 \times 10^{-4}$, but $C_{\rm{{Y}}}$ and $C_{\rm{{L}}}$ are out of phase in the same portion of the time-frequency domain. Since these regions of high cross-correlation are visible at a very low frequency (even lower than that characteristic of the switch between the bi-stable states), they can be used to infer the existence of a quasi-steady relationship between the different components of the aerodynamic force.

Fig. 4

Spatial distribution of the first 3 POD modes extracted from the base pressure distribution (top row), PIV cross-plane at $x^{*}=2.31$ (central row), PIV cross-plane at $x^{*}=3.31$ (bottom row) for $\psi = 0.0^{\circ }$. The modes are ordered according to their topology: a lateral symmetry breaking mode, b vertical symmetry breaking mode, and c planar symmetry preserving mode. $\delta C_{\rm{{p}}}$ refers to the magnitude of the spatial eigen-modes extracted from the field of the pressure fluctuation. The eigen-functions related to the velocity fluctuation are coloured according to the values of the through-plane component $\delta u^{*}$, whereas the streamlines are drawn considering the in-plane components $\delta v^{*}$ and $\delta w^{*}$

Fig. 5

Spectra of the temporal coefficients associated with the first three POD modes for $\psi = 0.0^{\circ }$ and $\psi =+ \, 0.6^{\circ }$. The curves have been shifted along the vertical axis

Fig. 6

Spatial distribution of the first three POD modes extracted from the base pressure distribution (top row), PIV cross-plane at $x^{*}=2.31$ (central row), PIV cross-plane at $x^{*}=3.31$ (bottom row) for $\psi = +0.6^{\circ }$. The modes are ordered according to their topology: a lateral symmetry breaking mode, b vertical symmetry breaking mode, and c planar symmetry preserving mode. $\delta C_{\rm {p}}$ refers to the magnitude of the spatial eigen-modes extracted from the field of the pressure fluctuation. The eigen-functions related to the velocity fluctuation are coloured according to the values of the through-plane component $\delta u^*$, whereas the streamlines are drawn considering the in-plane components $\delta v^*$ and $\delta w^*$

Fig. 7

Distribution of the normalised streamwise component of the vorticity ${{\varOmega }_{x}}^{*}$ over the PIV planes acquired at $x^{*}=2.31$ and $x^{*}=3.31$ for a one of the two conditionally averaged POD-filtered fields (R-State) and b the time-averaged field at $\psi = + \, 0.6^{\circ }$. c Schematic representation of one of two reflectional symmetry breaking states (L-State). In a and b, the streamlines are drawn considering the in-plane components of the velocity field. In c, the streamwise PIV planes are those already presented in Perry et al. (2016b); each plane is associated with a different colour, i.e., vortices on the same plane share the same colour

3.3 Characterisation of the wake dynamics

The wake dynamics were further investigated by applying POD to the fluctuating part of both pressure and PIV data for the two yaw angles considered in the present study. Only the first three modes are considered, as they represent about 80 and $60 \%$ of the overall energy captured by the pressure fluctuation on the base, respectively, at $\psi = 0.0^{\circ }$ and $\psi = + \, 0.6^{\circ }$; with the first mode at $\psi = 0.0^{\circ }$ accounting for twice as much energy as the same mode at $\psi = + \, 0.6^{\circ }$ due to the weakening of the bi-stable mode. The eigen-functions related to these modes are presented in Fig. 4 for $\psi = 0.0^{\circ }$ and Fig. 6 for $\psi =+ \, 0.6^{\circ }$; the spectrum of the related temporal coefficients is reported in Fig. 5.

For $\psi =0.0^{\circ }$, the first POD mode is a lateral symmetry breaking mode, since it is dominated by a left-to-right asymmetry associated with the action of both the bi-stable mode and the von Karman lateral vortex shedding (Volpe et al. 2015). The asymmetry visible from the pressure field can be seen to extend for the entire length of the wake on both of the PIV cross-planes (Fig. 4a). The $1{\rm{{st}}}$ eigen-function extracted from the velocity fields is dominated by two counter-rotating vortices aligned along the horizontal direction, matching that extracted from the mid-horizontal PIV plane by Perry et al. (2016b). These structures are centred with the model base and yield variations in the longitudinal component of the velocity $u^{*}$ that match the fluctuations over the base itself. Their size tends to reduce downstream due to the thickening of the side shear layers, in agreement with the findings of Gentile et al. (2016).

Similar conclusions can be drawn from the $3{\rm {rd}}$ mode extracted from the base pressure distribution and the $3{\rm{{rd}}}$ and $2{\rm{{nd}}}$ spatial modes obtained, respectively, from the first ($x^{*}=2.31$) and second ($x^{*}=3.31$) PIV plane. These fields are characterised by a strong top–bottom asymmetry (Fig. 4b), defining a vertical symmetry breaking POD mode.

The symmetry in the two transverse directions is almost fully restored when the $2{\rm{{nd}}}$ and $3{\rm{{rd}}}$ POD modes extracted from the velocity fields located respectively at $x^{*}=2.31$ and $x^{*}=3.31$ are considered (Fig. 4c), justifying the term of planar symmetry preserving POD mode. In this case, two pairs of counter-rotating vortices appear in the two PIV planes, suggesting the existence of the ovalisation mode of the rear recirculation already described by Gentile et al. (2016) for the wake past an axisymmetric body. This quadrupole structure is accompanied with the presence of out-of-phase variations in the streamwise component of the velocity $u^{*}$ between the central portion and the outermost sections of each plane, associated with the wake pumping. A similar distribution is extracted for the $2{\rm{{nd}}}$ mode of the pressure data.

When the model is yawed by $+ \, 0.6^{\circ }$, the structures previously described are still recognisable, but the left–right and top–bottom asymmetries are now much closer in terms of energy content, due to the weakening of the bi-stable mode and the decrease of its contribution to the fluctuations in the lateral direction. The asymmetric constraint imposed by the model yaw shifts the regions with the highest level of fluctuation towards the windward side accompanied with a stable vortical structure formed along the leeward side, as mentioned in Sect. 3.1. By analysing this case, it can be inferred that the fluctuations originating from the short-time motions of the wake in the lateral and vertical direction are the result of the interactions between this vortical structure and the shear layers emanating from the windward side of the base. In a similar way, the fluctuations in the two transverse directions seen at $\psi = 0.0^{\circ }$ are the result of the superimposition of the interactions between each one of the bi-stable states and the shear layer emanating from the opposite side of the model.

The power spectral density (PSD) of the temporal coefficients of the same POD modes (Fig. 5) shows that in all cases, the turbulent logarithmic decay is captured above ${{\rm{St}}_{\rm {H}}}> 0.3$. The two spikes appearing at $0.7<{{\rm{St}}_{\rm {H}}}< 0.8$ are due to the resonant frequencies of the flexible tubing. The presence of the bi-stable mode is confirmed by the $- \, 2$ law describing the decrease of the energy captured by the $1{\rm{{st}}}$ mode at very low frequency for $\psi = 0.0^{\circ }$, confirming the findings of Grandemange (2013). In the first mode, two peaks occur at ${{\rm{St}}_{\rm {H}}} = 0.07$ and ${{\rm{St}}_{\rm {H}}} = 0.13$, but in the second and third modes, the latter is replaced with a peak at ${{\rm{St}}_{\rm {H}}} = 0.19$. This confirms the existence of three distinct coherent motions of the wake in addition to the bi-stable mode, matching the results of the experiments performed by Volpe et al. (2015) for similar values of ${{\rm{Re}}_{\rm {H}}}$.

Table 1 Locations of the centres of the vortical structures captured by the PIV planes located at $x^{*}=2.31$ and $x^{*}=3.31$: (a) R-State for $\psi = 0.0^{\circ }$; (b) time-averaged field for $\psi = + \, 0.6^{\circ }$

3.4 Topology of the bi-stable states

The two bi-stable states were isolated from the PIV data using the approach presented in Perry et al. (2016b); a low-order model was constructed from the time-averaged field and the first POD mode according to the following equation:

$$\begin{aligned} {\mathbf {F}}^{\rm{{LOM}}} ({\mathbf {x}}, t) = {\mathbf {F}}_0({\mathbf {x}}) + a_1(t){{\mathbf {\phi}} _1}({\mathbf {x}}). \end{aligned}$$

(6)

The realisations obtained ${\mathbf {F}}^{\rm{{LOM}}} ({\mathbf {x}}, t)$ were filtered from the noise using a moving average filter with a cut-off frequency of $1 \, {\rm{{Hz}}}$ and sorted according to the value of the first temporal coefficient $a_1(t)$, based on the condition $a_1(t) \le \tau$ or $a_1(t)> \tau$, where $\tau = ({\rm{{max}}}(a_1(t)) + {\rm{{min}}}(a_1(t)))/2$. The fields within each group were then averaged. The results related to the Right State (R-State) are presented in Fig. 7a, coloured according to the values of the streamwise component of the normalised vorticity ${\tilde{\varOmega }_{x}}^{*} = \frac{\partial w^{*}}{\partial y^{*}} - \frac{\partial v^{*}}{\partial z^{*}}$. On each plane, the location of the cores of the vortical structures was determined by applying the $\varGamma _{1}$ criterion proposed by Graftieaux et al. (2001), based on the detection of the local maximum of the function 7:

$$\begin{aligned}{{\mathbf {\Gamma}} _{1}} ({\mathbf {P}}^{*}) = \frac{1}{N_{\rm{{p}}}} \int _{{\mathbf {M}}^{*} \in S^{*}_{\varGamma _1}} \frac{({\mathbf {PM}}^{*} \wedge{{\mathbf {V}}_{\rm {M}}}^{*}) \times {\mathbf {n}}}{\Vert {{\mathbf {PM}}^{*}}\Vert \times \Vert {{{\mathbf {V}}_{\rm {M}}}^{*}}\Vert} {\rm{{d}}}S^{*}_{\Gamma _1}, \end{aligned}$$

(7)

where ${{\mathbf {P}}^{*}}$ is a fixed point in the measurement domain, $S^{*}_{\varGamma _1}$ is a rectangular domain of fixed size surrounding ${{\mathbf {P}}^{*}}$, $N_{\rm{{p}}}$ is the number of points ${{\mathbf {M}}^{*}}$ inside ${{S_{I}}^{*}}$, ${\mathbf {n}}$ is the unit vector normal to the measurement plane, and ${{\mathbf {V}}_{\rm {M}}}^{*}$ is the in-plane velocity vector. The circulation around each core was then determined as $\varGamma ^{*} = \int _{S^{*}_{{\varGamma }^{*}}} {{\varOmega }_{x}}^{*} {\rm{{d}}}S^{*}_{{\varGamma }^{*}}$, where $S^{*}_{{\varGamma }^{*}}$ is a squared region with sides of normalised length equal to 0.1 surrounding each vortex core. For comparison, the time-averaged field obtained for $\psi = + \, 0.6^{\circ }$ (Fig. 7b) was considered too. The results for both cases are reported in Table 1.

A very similar wake organisation is seen between the two cases for the cross-plane at $x^{*} = 2.31$, with two counter-rotating vortical structures acting close to the right-hand side of the model base. These structures have similar strengths, as highlighted by the magnitude of the values of the normalised circulation $\varGamma ^{*}$ reported in Table  1, with the upper structure (rotating in the clockwise direction) always slightly prevailing over the bottom one (rotating counterclockwise). Bigger differences are seen when the cross-plane further downstream of the model base (at $x^{*} = 3.31$) is considered. In this case, two vortical structures can still be recognised for the time-averaged field associated with the model tested at $\psi = + \, 0.6^{\circ }$, although they are now placed at the opposite side of the base (see Sect. 3.1). Compared to the plane at $x^{*} = 2.31$, the vertical distance between the cores of the vortex is now reduced, as a consequence of the tapering of the wake, and the difference in the value of $\overline{\varGamma }^{*}$ between the upper and lower structure is accentuated (with the former still prevailing over the latter). Nevertheless, the continuity in the sign $\overline{\varOmega }_{x}^{*}$ (and, therefore, circulation) between the vortices acting in correspondence of the same horizontal portions of each plane indicates that they are part of the same “leg” extending downstream of the base. The difference in circulation between the two vortices seen at $x^{*} = 3.31$ for $\psi = + \, 0.6^{\circ }$ increases even further in the case of the conditional averaged state, where only the upper core is detected by the $\varGamma _{1}$ criterion.

The structure of the bi-stable state becomes clearer when the two stereoscopic PIV cross-planes considered in the present work are combined with the PIV fields presented in Perry et al. (2016b) (Fig. 7). Each mode consists of a hairpin vortex that is the result of the combination of the “slow” transverse vortex and the “fast”’ “C” shaped vortex proposed by Perry et al. (2016b). This vortical structure forms parallel to one of the two vertical sides of the base and then splits into two legs that bend horizontally while moving downstream, until they reach the opposite side of the base, with the top leg eventually prevailing over the bottom one. This topology presents some analogies with that speculated by Evrard et al. (2016), but in this case, all the vortices captured by the PIV planes have been included in the structure, thanks to a more complete set of data. A similar organisation has been seen in the wake of a sphere for ${\rm{{Re}}}> 280$ (Chrust et al. 2013). These structures have been shown to originate from the symmetry breaking mode that appears at ${\rm{{Re}}} \approx 210$ (Magarvey and Bishop 1961) and have been linked to the multi-stable behaviour seen for the same geometry at high Reynolds numbers (Grandemange et al. 2014a). Furthermore, their presence seems to explain the formation of the two counter-rotating vortices forming downstream of the closure of the time-averaged wake, seen in Sect. 3.1.

Fig. 8

Coherence analysis performed considering the unsteady signal recorded by pressure taps placed at different locations along the trailing edges of the model base for $\psi = 0.0^{\circ }$: a top-left tap vs bottom-left tap, top-centre tap vs bottom-centre tap, top-right tap vs bottom-right tap; b top-left tap vs top-right tap, mid-left tap vs mid-right tap, bottom-left tap vs bottom-right tap

Fig. 9

Coherence analysis performed considering the unsteady signal recorded by pressure taps placed at different locations along the trailing edges of the model base for $\psi = + \, 0.6^{\circ }$: a top-left tap vs bottom-left tap, top-centre tap vs bottom-centre tap, top-right tap vs bottom-right tap; b top-left tap vs top-right tap, mid-left tap vs mid-right tap, bottom-left tap vs bottom-right tap; c top-centre tap vs top-right tap, bottom-centre tap vs bottom-right tap; d top-centre tap vs top-left tap, bottom-centre tap vs bottom-left tap

Fig. 10

Schematic representation of the proposed interpretation for the “wake pumping”

3.5 Characterisation of the short-time wake dynamics

To understand better the nature of the motions associated with short-time wake dynamics, the coherence between signals recorded by taps placed in different locations along the trailing edges of the model was considered, following the approach used by Duell and George (1999). The magnitude of the coherence between two generic synchronised signals i and j was calculated according to the equation:

$$\begin{aligned} {{\mathbf {\Lambda}}_{ij}} (f) = \frac{{|{{{\mathbf {P}}_{ij}}(f)}|}^2}{{{\mathbf {P}}_{ii}}(f) \times {{\mathbf {P}}_{jj}}(f)}, \end{aligned}$$

(8)

where ${{\mathbf {P}}_{ij}}(f)$ is the cross-spectrum and ${{\mathbf {P}}_{ii}}(f)$ and ${{\mathbf {P}}_{jj}}(f)$ are the auto-spectra of the signals. The phase relationship between the two signals was then determined as follows:

$$\begin{aligned} {{\mathbf {\Theta}} _{ij}} (f) = \left|{ \tan ^{-1}{\left( {\frac{\rm{{Im}} \left( {{\mathbf {P}}_{ij}(f)} \right) }{\rm{{Re}} \left( {{\mathbf {P}}_{ij}(f)}\right) } }\right) } } \right|, \end{aligned}$$

(9)

considering for simplicity the absolute value of the phase angle. The results for $\psi = 0.0^{\circ }$ and $\psi = + \, 0.6^{\circ }$ are reported in Figs. 8 and 9.

At Strouhal numbers between 0.0 and 0.1, a good level of correlation exists between the tapping at top-centre (TC) and bottom-centre (BC), with a clear peak at ${{\rm{St}}_{\rm {H}}} \simeq 0.07$ and a phase angle fixed at $0 \, {\rm{{rad}}}$ (Fig. 8a). Towards the sides of the model, the correlation between the top and bottom edges of the base decreases, although the peak at ${{\rm{St}}_{\rm {H}}}=0.07$ is still recognisable. In these regions, a second peak appears at ${{\rm{St}}_{\rm {H}}}=0.19$, with a phase angle $\varTheta (f) \approx \pi \, {\rm{{rad}}}$ that confirms the flapping nature of the coherent motion associated with this frequency. The fact that this last peak is only visible close to the sides of the model supports the thesis that the vertical flapping is the result of the interaction between the two bi-stable states and the top and bottom shear layers emanating from the opposite half of the model base. This is confirmed when the model is yawed to $\psi = + \, 0.6^{\circ }$, as this peak remains visible only in the correlation between the taps placed on the windward side of the base (Fig. 9a, b).

The ${{\rm{St}}_{\rm {H}}}=0.07$ peak is still present when the cross-correlation is performed between the top-left (TL) and top-right (TR) taps as well as the bottom-left (BL) and bottom-right (BR) taps, with the model at $\psi = 0.0^{\circ }$. In this case, however, the signals recorded on opposite sides of the base are out of phase (Fig. 8b). Instead of the peak at ${{\rm{St}}_{\rm {H}}} = 0.19$, a new peak appears at ${{\rm{St}}_{\rm {H}}} = 0.13$. This last peak is the only one that is visible when the cross-correlation is performed between the mid-left (ML) tap and the mid-right (MR) tap and its phase angle of $\varTheta (f) \approx \pi \, {\rm{{rad}}}$ confirms that it is associated with the lateral flapping of the wake closure.

The nature of the motion associated with ${{\rm{St}}_{\rm {H}}}=0.07$ becomes clearer when the case with the model yawed to $\psi = + \, 0.6^{\circ }$ is considered. This is illustrated for TC-TR and BC-BR in Fig. 9c and for TC-TL and BC-BL in Fig. 9d. For this value of the normalised frequency, it is shown that a strong correlation exists between the taps of the first two pairs, with a $0 \, {\rm{{rad}}}$ phase angle; the level of correlation, however, decreases noticeably when the other two pairs of taps are considered, whilst the phase increases to $\pi \, {\rm{{rad}}}$.

All these information allows for the formulation of a more accurate description of the wake pumping than that provided in previous works (Duell and George 1999; Volpe et al. 2015). This coherent motion is actually the result of the reciprocal interaction of the inner portions of the hairpin vortex that forms each bi-stable state. As a consequence, the vortex itself is “stretched” and “squeezed” in the streamwise direction, yielding pressure variations over the model base that have opposite signs between the left- and right-hand portion of the base but share the same sign within each side. For example, when the vortex associated with the L-state is “stretched” (Fig. 10a), its core is squeezed towards the left-hand portion of the base, yielding a drop in the value of $C_{\rm{{p}}}$ in that area; simultaneously, it is moved further away from the base on the opposite side, allowing an increase in the static pressure in that area. The direction of the motion is reversed when the same vortex is “squeezed” (Fig. 10b).

Fig. 11

Scatter plots of the temporal coefficients associated with the first three POD modes extracted from the base pressure data recorded for $\psi = 0.0^{\circ }$: a $a_2(t)$ vs $a_1(t)$; b $a_3(t)$ vs $a_1(t)$; c $a_2(t)$ vs $a_3(t)$. The colour map shows the probability density function (PDF) distribution of the values of the considered coefficients

Fig. 12

a Scatter plot of the POD temporal coefficients associated with the lateral symmetry breaking mode $a_1(t)$ and the vertical symmetry breaking mode $a_3(t)$, extracted from the PIV data; b values of $a_1(t)$ and $a_3(t)$ sorted along the phase angle $\theta$; c number of snapshots contained in each bin ($\Delta \theta = 15^{\circ }$)

3.6 Characterisation of the symmetric state

The scatter plots of the temporal coefficients related to the first three POD modes (Fig. 11) provide information concerning the dynamics of the switch between the two bi-stable states. The relationship between the lateral symmetry breaking mode $a_1(t)$ and the planar symmetry preserving mode $a_2(t)$ (Fig. 11a) shows that $a_2(t)$ reaches its highest positive values only when the first mode is deactivated ($a_{1}(t) \rightarrow 0$). This, combined with the fact that the $2{\rm{{nd}}}$ POD mode describes the longitudinal motion of the wake, suggests that a reduction of the interaction between the core of the vortical structure and the base is achieved any time that the lateral asymmetry is suppressed. A similar relationship is not found between the vertical symmetry breaking mode $a_3(t)$ and the planar symmetry preserving mode $a_2(t)$ (Fig. 11c). Furthermore, the restoration of the lateral symmetry does not imply the deactivation of the vertical asymmetry, as seen in the distribution of the scatter plot between $a_3(t)$ and $a_1(t)$ reported in Fig. 11b.

Applying the same approach to the PIV data at $x^{*}=2.31$ (Fig. 12a) produces a distribution similar to that obtained by Gentile et al. (2016) for the first two modes extracted from stereoscopic PIV cross-planes at a similar distance from the base of an axisymmetric body. In the axisymmetric body case, the symmetry breaking mode takes all azimuthal positions, so that the values of the temporal coefficients related to the two symmetry breaking modes are arranged around a uniform circular pattern, whereas here, the data tend to cluster around two distinct attractors, as the base aspect ratio allows the selection of only two stable asymmetric states (Grandemange and Gohlke 2013a). However, since there is still a dispersion of points around the centre of the plot and the related spatial modes are in quadrature, it was decided to fit $a_1(t)$ and $a_3(t)$ with a pair of trigonometric functions, such that the temporal coefficients could be reordered in phase (see Fig. 12b) following an approach similar to that proposed by Van Oudheusden et al. (2005) and Legrand et al. (2011).

The fitting was done according to the equations:

$$\left(\mathbf{\alpha_1} - r \cos \left(\frac{2 \pi \mathbf{\chi}}{N_s} \right) \right)^2 + \left(\mathbf{\alpha_3} - r \sin \left(\frac{2 \pi \mathbf{\chi}}{N_s} \right) \right) ^2 = min,$$

(10)

$$\begin{aligned}&{\mathbf {\theta}} = \frac{2 \pi {\mathbf {\chi }}}{N_{\rm{{s}}}} \frac{\pi }{180}, \end{aligned}$$

(11)

where $r = \sqrt{2/N_{\rm{{s}}}}$, and ${{\mathbf{\alpha}}_1}$ and ${{\mathbf{\alpha}}_2}$ are the eigenvectors obtained from the POD for the lateral and vertical symmetry breaking modes. A low-order model, consisting of the time-averaged field and the first three POD modes, was then created after having averaged the fluctuating terms in bins of $15^{\circ }$. This is similar to the approach using a conditional average performed by Grandemange (2013) for the wake of a spherical body. The results obtained for eight $\pi /4\, {\rm{{rad}}}$ increments of the phase angle $\theta$ are presented in Figs. 13 and 14 for $x^{*}=2.31$ and $x^{*}=3.31$, summarising all the configurations of the wake during its unsteady evolution. They are not a reconstruction of a particular periodic behaviour, as the succession of the bi-stable states seems to be a weak chaotic process (Varon et al. 2017). Nevertheless, they still provide insights into how the wake evolves between states. From the results, in fact, four main states can be isolated: the two bi-stable states (at $\theta = 0\, {\rm{{rad}}}$ and $\theta = \pi \, {\rm{{rad}}}$) and two symmetric states (at $\theta = \pi /2\, {\rm{{rad}}}$ and $\theta = 3/2 \pi \, {\rm{{rad}}})$, whose presence is a necessary, but not sufficient, condition for the switch between the first two states. The distribution of the number of snapshots contained in each bin (Fig. 12c) shows for the plane at $x^{*}=2.31$ a clear prevalence of the bi-stable states, with the one centred around $\theta = 0\, {\rm{{rad}}}$ occurring more often than that at $\theta = \pi$, justifying the slight lateral asymmetry already discussed for the time-averaged results in Sect. 3.1. There are not big differences, however, in the number of occurrences associated with the two symmetric states, confirming the weak nature of the interactions between the ground plane and the wake.

Each bi-stable state evolves in time, changing continuously due to the action of the dynamic modes, and the balance between the two recirculations that form the streamwise legs of the hairpin vortices is alternately lost and recovered until one of the two structures eventually prevails, yielding the definitive loss of symmetry on the horizontal plane. As the wake loses its vertical symmetry, the symmetry in the lateral direction is recovered leading to the establishment of one of the symmetric states ($\theta = \pi /2\, {\rm{{rad}}}$ and $\theta = 3/2 \pi \, {\rm{{rad}}}$ in Figs. 13, 14). At this point, the system is in a condition of unstable equilibrium and can either return to the previous bi-stable state or switch to the opposite one, depending on any random perturbation (Brackston et al. 2016). From a topological point of view, the transition from a bi-stable state to a symmetric state resembles the evolution from the steady symmetric state to the steady asymmetric state reported by Grandemange (2013) for the laminar wake past an Ahmed body, confirming the laminar origin of this particular instability. In any case, the wake never recovers its full symmetry, since the topology of the most symmetric state is always dominated by either the upper or lower recirculation depending on the random perturbation that triggers the transition from the bi-stable state to the symmetric state: a perturbation originating in the lower portion of the bi-stable state will result in a symmetric state dominated by the bottom recirculation, whilst a perturbation originating from the upper part of the bi-stable state will lead to a symmetric state dominated by the upper lobe.

Fig. 13

Low-order phase-averaged velocity field for $x^{*}=2.31$. The plots are coloured according to the values of the normalised streamwise component of the vorticity ${\tilde{\varOmega }_{x}}^{*}$; the streamlines are drawn considering the in-plane components of the velocity field

Fig. 14

Low-order phase-averaged velocity field for $x^{*}=3.31$. The plots are coloured according to the values of the normalised streamwise component of the vorticity ${\tilde{\varOmega }_{x}}^{*}$; the streamlines are drawn considering the in-plane components of the velocity field

The fact that a strong asymmetry is present between the upper and lower portions of the wake any time the lateral symmetry is restored supports the thesis that the bi-stable mode is, indeed, the result of the interaction between the two horizontal shear layers, as identified by Cadot et al. (2015) for a similar model. This asymmetry extends over the entire wake, yielding either a slightly upwash or downwash dominated wake every time the lateral asymmetry is suppressed (Fig. 14). This also accords with the cross-wavelet analysis where the out-of-phase relationship between $C_{\rm{{Y}}}$ and $C_{\rm{{L}}}$ suggests an increase in the magnitude of the vertical force as the lateral force tends to zero, consistent with the switching between the laterally asymmetric and symmetric states identified in the phase-averaged PIV fields.

Fig. 15

Scatter plots between the unsteady values of the pressure drag obtained from the low-order model ${C}^{\rm{(POD)}}_{{\rm{D}}_{\rm {Rear}}}(t)$ and the temporal coefficients associated with the first three POD pressure modes for $\psi = 0.0^{\circ }$: a ${C}^{\rm{(POD)}}_{{\rm{D}}_{\rm {Rear}}}(t)$ vs $a_1(t)$; b ${C}^{\rm{(POD)}}_{{\rm{D}}_{\rm {Rear}}}(t)$ vs $a_2(t)$; c ${C}^{\rm{(POD)}}_{{\rm{D}}_{\rm {Rear}}}(t)$ vs $a_3(t)$. The colour map shows the PDF distribution of the values of the considered coefficients

3.7 Effect of the symmetric state on the base drag

The in-phase relationship identified between $C_{\rm{{Y}}}$ and $C_{\rm{{D}}}$ in Sect. 3.2 was further investigated by looking at the contribution of the three POD modes described in Sect. 3.3 to the rear drag $C_{{\rm{D}}_{\rm {Rear}}}$. Using a low-order model for the pressure data $C^{\rm{{(POD)}}}_{{\rm{p}}_{\rm {i}}}(t)$ (consisting of the time-averaged base pressure distribution and the first three POD modes), the corresponding rear drag ${C}^{\rm{{(POD)}}}_{{\rm{D}}_{\rm {Rear}}}(t)$ (estimated using Eq. 5 replacing $\overline{C}_{{\rm{p}}_{\rm {i}}}$ with $C^{\rm{{(POD)}}}_{{\rm{p}}_{\rm {i}}}(t)$) was correlated with the temporal coefficients of the same POD modes, leading to the scatter plots reported in Fig. 15.

The correlation of ${C}^{\rm{{(POD)}}}_{{\rm{D}}_{\rm {Rear}}}(t)$ and $a_{1}(t)$ (Fig. 15a) shows that a drag reduction can be achieved any time that the lateral symmetry of the wake is restored; namely, $a_{1}(t) \rightarrow 0$. A similar conclusion was drawn by Evrard et al. (2016) and Li et al. (2016). A deeper understanding of the origin of this drag reduction can be achieved by looking at the scatter plot between ${C}^{\rm{{(POD)}}}_{{\rm{D}}_{\rm {Rear}}}(t)$ and $a_{2}(t)$ (Fig. 15b). An almost linear relationship exists between the base drag and the temporal coefficients associated with the planar symmetry preserving POD mode, with the lowest value of ${C}^{\rm{{(POD)}}}_{{\rm{D}}_{\rm {Rear}}}(t)$ obtained when $a_{2}(t)> 0$. This, combined with the fact that $a_{2}(t)$ assumes its highest positive values when the switch between the two bi-stable modes is most likely to occur (as seen in Sect. 3.6), confirms that the drag reduction associated with the restoration of the wake lateral symmetry comes from the weakening of the interaction between the core of the recirculating structures and the base of the model, rather than just from the suppression of the lateral asymmetry. No particular correlation exists between ${C}^{\rm{{(POD)}}}_{{\rm{D}}_{\rm {Rear}}}(t)$ and $a_3(t)$ (Fig. 15c), in agreement with that already stated in Sect. 3.6.

Fig. 16

Low-order phase-averaged velocity field for $z^{*}=0.67$. The plots are coloured according to the values of the normalised vertical component of the vorticity ${\tilde{\varOmega }_{z}}^{*}$; the streamlines are drawn considering the streamwise and spanwise components of the velocity field. PIV data from Perry et al. (2016b)

Fig. 17

Base pressure distribution corresponding to the suppression of the bi-stable mode

The weakening of the interaction between the vortical structures and the base, occurring any time the wake recovers its lateral symmetry, can also be seen from the evolution of the low-order phase-averaged velocity field obtained by applying the same technique described in Sect. 3.6 to the 2D-2C PIV data recorded by Perry et al. (2016b) along a horizontal plane centred with the wake (Fig. 16). In this case, the low-order model was built using the first four POD modes; their temporal coefficients were ordered in phase according to Eq. 10 using the $1{\rm{{st}}}$ mode and $4{\rm{{th}}}$ mode as sorting modes, because in this case, the vertical symmetry breaking mode has a much lower energy level as there is no through-plane velocity component. The results show that as the lateral asymmetry is suppressed, the large recirculation close to the base in each bi-stable state is stretched downstream and becomes narrower, whilst a change in the opposite direction can be observed for the recirculation farther from the base, in good agreement with the description provided in Sect. 3.5 for the pumping mode. These changes lead eventually to the restoration of the symmetry between the two sides of the wake. At this point, the reverse flow impinging on the base is at its maximum, allowing a better pressure recovery and lower aerodynamic drag, confirming the in-phase relationship between $C_{\rm{{Y}}}$ and $C_{\rm{{D}}}$ seen in Sect. 3.2: as the lateral symmetry is restored, $C_{\rm{{Y}}} \rightarrow 0$ and $C_{\rm{{D}}}$ reaches its minimum value.

The drag reduction associated with the suppression of the lateral asymmetry was quantified by averaging the base pressure distributions obtained from the low-order model for the condition $0.1 \times {\rm{{min}}}(a_1(t)) \le a_1(t) \le 0.1 \times {\rm{{MAX}}}(a_1(t))$. The resulting base pressure distribution (Fig. 17) is characterised by an increase in both size and magnitude of the “high”-pressure region corresponding to the rear stagnation, compared to the pressure distribution resulting from the time average of the entire data set (Fig. 2a). Two low-pressure regions, however, are still visible close to the vertical sides of the base, matching the locations of the recirculating structures seen from the phase-averaged velocity fields when the bi-stable state is suppressed (Figs. 13, 14, 16). This base pressure distribution yields a $7 \%$ reduction over the time-averaged base drag ($\tilde{C}^{\rm{{{(POD)}}}}_{{{\rm{D}}_{\rm {Rear}}}(S)}$, Table 2). This is in line with the $8 \%$ decrease estimated by Li et al. (2016) and the $6 \%$ reduction obtained by Grandemange et al. (2014b) stabilising the wake using a vertical control cylinder. A slightly higher improvement of $\overline{C}_{{\rm{D}}_{\rm {Rear}}}$ was obtained by Evrard et al. (2016) applying a cavity at the base of a similar geometry, arguably as a consequence of the further weakening of the interaction between the model base and the vortical structure due to the depth of the cavity.

Table 2 Average values of the base drag

The time-averaged value of the pressure drag (Table 2) obtained from both the unfiltered ($\overline{C}_{{\rm{D}}_{\rm {Rear}}}$) and filtered ($\overline{C}^{\rm{{(POD)}}}_{{\rm{D}}_{\rm {Rear}}}$) data set is 0.004 higher than that reported for the same geometry in Pavia et al. (2016), due to the coarser distribution of pressure taps used in the present study. Nevertheless, the results obtained are in good agreement with the trends in the previous studies. In particular, the equality between the time-averaged pressure drag and the mean pressure drag associated with each one of the two bi-stable states observed in Pavia et al. (2016) is still present. This can be seen from the values of $\tilde{C}^{\rm{{(POD)}}}_{{{\rm{D}}_{\rm {Rear}}}(L)}$ and $\tilde{C}^{\rm{{(POD)}}}_{{{\rm{D}}_{\rm {Rear}}}(R)}$, calculated by averaging the fields extracted from the filtered data set under the conditions $a_1(t) < 0.1 \times {\rm{{min}}}(a_1(t))$ and $a_1(t)> 0.1 \times {\rm{{MAX}}}(a_1(t))$ and further confirms that the only source of drag reduction is found in the transition between the bi-stable states.

4 Summary and conclusions

An extensive experimental campaign consisting of balance, pressure, and 2D-3C particle image velocimetry was carried out using the Windsor body at ${{\rm{Re}}_{\rm {H}}} = 7.7 \times 10^{5}$ to investigate the dynamics of the wake and in particular the bi-stable behaviour.

The application of proper orthogonal decomposition to the fluctuating part of the base pressure and PIV data has shown the existence of coherent motions of the wake in three directions: a lateral symmetry breaking mode, a vertical symmetry breaking mode, and a planar symmetry preserving mode.

Subsequent analysis confirms that these POD modes are the result of the combination of the long-time period bi-stable mode described in Grandemange et al. (2012a), the global oscillating modes identified in Grandemange et al. (2013b), and the pumping mode described in Duell and George (1999). This fact also highlights the existence of remarkable similarities between the wake generated by the Windsor body used in the present work and that of the geometry proposed by Ahmed et al. (1984) employed in the previous studies.

The global oscillating modes consist of lateral and vertical motions of the wake closure with normalised frequencies of ${{\rm{St}}_{\rm {H}}} = 0.13$ and ${{\rm{St}}_{\rm {H}}} = 0.19$ and originate from the interactions between the hairpin vortex that forms each one of the two bi-stable states and either the vertical or horizontal shear layers originating from the opposite side of the model base.

The pumping mode, with a characteristic frequency of ${{\rm{St}}_{\rm {H}}} = 0.07$, results from the interaction between the inner regions of each hairpin vortex as it bends downstream moving far from the model base. Due to the action of this mode, the hairpin vortices are alternately “stretched” and “squeezed” in the streamwise direction, yielding out-of-phase variations in the static pressure between the left-hand side and right-hand side portions of the base.

A phase-averaged low-order model constructed from the time-averaged field and first three POD modes has been used to isolate all the configurations assumed by the wake during its evolution. It is shown that the bi-stable mode can be described as a result of the combination of the lateral and vertical symmetry breaking POD modes.

When the wake recovers its lateral symmetry, two different laterally symmetric states appear, depending on the random perturbation that triggers the transition from the bi-stable asymmetric state to the symmetric state: a perturbation originating in the lower portion of the laterally asymmetric state will result in a symmetric state dominated by the bottom recirculation, whilst a perturbation originating from the upper part of the laterally asymmetric state will lead to a symmetric state dominated by the upper lobe. As a result, a quasi-steady out-of-phase relationship is seen between side force and lift when cross-wavelet transform is applied to the signals referring to these two components of the aerodynamic force.

When the wavelet cross-spectrum of side force and drag is considered, a quasi-steady in-phase relationship is found. The origin of this relationship can be ascribed to the reduction of the interaction between the recirculating structures and the base occurring any time the wake switches from a bi-stable state to a symmetric state, resulting in a $7 \%$ decrease of the base drag compared to the time-averaged value. This potential gain motivates the application of flow control strategies aiming to stabilising the symmetric state, as proposed for example by Grandemange et al. (2014b), Evrard et al. (2016), Li et al. (2016), and Brackston et al. (2016) and suggests the existence of an additional margin for improvement in those cases where the actuated flow is still asymmetric, as in Littlewood and Passmore (2012) and Barros et al. (2016).

Furthermore, the results of the findings presented in this work seem to suggest that a certain degree of pumping motion is “needed” to trigger a switch when the wake is in a condition of “almost perfect symmetry”, but is not enough when the system is forced towards one of the laterally asymmetric states (for example by yawing the model). This interpretation of the pumping may explain the ability of base cavities to mitigate or even suppress the bi-stable mode (Evrard et al. 2016). In this case, in fact, the suppression of bi-stability may be a direct consequence of dampening of the motion of the wake in the streamwise direction described by Duell and George (1999).