1 Introduction

Estimation from available data of model parameters describing epidemic dynamics is a major challenge in epidemiology, especially contributing to better understand the mechanisms underlying these dynamics and to provide reliable predictions. Epidemics can be recurrent over time and/or occur simultaneously in different regions. For example, influenza outbreaks in France are seasonal and can unfold in several distinct regions with different intensities at the same time. This translates into a non-negligible variability between epidemic phenomena. In practice, this inter-epidemic variability is often omitted, by not explicitly considering specific components for each entity (population, period). Instead, each data series is analysed separately and this variability is estimated empirically. Integrating in a unique model these sources of variability allows to study simultaneously the observed data sets corresponding to each spatial (e.g. region) or temporal entity (e.g. season). This approach should improve the statistical power and accuracy of the estimation of epidemic parameters as well as refine knowledge about underlying inter-epidemic variability.

An appropriate framework is represented by the mixed-effects models, which allow to describe the variability between subjects belonging to a same population from repeated data (see e.g. Pinheiro and Bates 2000; Lavielle 2014). These models are largely used in pharmacokinetics with intra-population dynamics usually modeled by ordinary differential equations (ODE) and, in order to describe the differences between individuals, random effects on the parameters ruling these dynamics (see e.g. Collin et al. 2020). This framework was later extended to models defined by stochastic differential equations incorporating mixed effects in the parameters of these diffusion processes (Donnet and Samson 2008, 2013; Delattre and Lavielle 2013; Delattre et al. 2018). To our knowledge, the framework of mixed-effects models has rarely been used to analyse epidemic data, except in a very few studies. Among these, in Prague et al. (2020), the dynamics of the first epidemic wave of COVID-19 in France were analysed using an ODE system incorporating random parameters to take into account the variability of the dynamics between regions. Using a different approach to tackle data from multiple epidemics, Bretó et al. (2020) proposed models that incorporate unit-specific parameters and shared parameters and studied a likelihood-based inference method using particle filtering techniques for non-linear and partially observed models. Indeed, various ways can be investigated to describe multiple epidemics. They differ according to the purpose. Modeling dependence between regional epidemics within the same country or between successive epidemic waves requires other models. The mixed-effect approach proposed here is a first step in the analysis of the variability present across epidemics. It presents the advantage over other models that it allows to avoid the well-known “curse of dimensionality” because of its parsimony in the model parameters.

In addition to the specific problem of variability reflected in multiple data sets, observations of epidemic dynamics are often incomplete in various ways: only certain health states are observed (e.g. infected individuals), data are temporally discretized or aggregated, and subject to observation errors (e.g. under-reporting, diagnosis errors). Because of this incompleteness together with the non-linear structure of the epidemic models, the computation of the maximum likelihood estimator (MLE) is often not explicit. In hidden or latent variable models which are appropriate representations of incompletely observed epidemic dynamics, estimation techniques based on Expectation-Maximization (EM) algorithm can be implemented in order to compute the MLE (see e.g. Dempster et al. 1977). However, the E-step of the EM algorithm requires that, for each parameter value \(\theta \), the conditional expectation of the complete log-likelihood given the observed data, \({\mathcal {Q}}(\theta )\), can be computed. In mixed-effects models, there is generally no closed form expression for \({\mathcal {Q}}(\theta )\). In such cases, this quantity can be approximated using a Monte-Carlo procedure (MCEM, Wei and Tanner 1990), which is computationally very demanding. A more efficient alternative is the SAEM algorithm (Delyon et al. 1999), often used in the framework of mixed-effects models (Kuhn and Lavielle 2005), which combines at each iteration the simulation of unobserved data under the conditional distribution given the observations and a stochastic approximation procedure of \({\mathcal {Q}}(\theta )\) [(see also Delattre and Lavielle (2013), Donnet and Samson (2014) for the study and implementation of the SAEM algorithm for mixed-effects diffusion models].

Data from epidemic dynamics are mostly noisy prevalence data (i.e. the number of cases of disease in the population at a given time or over a given period of time) or noisy incidence data (i.e. the number of newly detected cases of the disease at a given time or over a given period of time). In this paper, our concern is to consider both types of data and, focusing on the inference for multiple epidemic dynamics, we intend to meet two objectives. The first objective is to propose a finer modeling of multiple epidemics through a unique mixed-effects model, incorporating a stochastic representation of each epidemic. The second objective is to develop an appropriate method for jointly estimating model parameters from noisy and partial observations, able to estimate rigorously and explicitly the inter-epidemic variability. Thus, the main expected contribution is to provide accurate estimates of common and epidemic-specific parameters and to provide elements for the interpretation of the mechanisms underlying the variability between epidemics of the same nature occurring in different locations or over distinct time periods. For this purpose, we extend the Gaussian state-space model introduced in Narci et al. (2021) for prevalence data of single epidemics to a model with mixed effects on the parameters describing simultaneously several epidemics and their observations. Then, following (Delattre and Lavielle 2013) and building on the Kalman filtering-based inference method proposed in Narci et al. (2021), we propose to couple the SAEM algorithm with Kalman-like filtering to estimate model parameters. Afterwards, in order to handle incidence data, we propose a new version of the filtering algorithm that is coupled with SAEM to estimate the parameters. The performances of the estimation method are investigated on simulations mimicking noisy prevalence data, and second noisy incidence data for SIR epidemics. The method is then applied to the case of influenza epidemics in France over several years: the underlying dynamics is described by a SEIR model and data consist of noisy incidence data from 1990 to 2017.

The paper is organized as follows. In Sect. 2 we describe the epidemic model for a single epidemic, specified for both prevalence and incidence data, and its extension to account for several epidemics through a two-level representation using the framework of mixed-effects models. Section 3 contains the maximum likelihood estimation method and convergence results of the SAEM algorithm. In Sect. 4, the performances of our inference method are assessed on simulated noisy prevalence data generated by SIR epidemic dynamics sampled at discrete time points. Section 5 is dedicated to the application case, the influenza outbreaks in France from 1990 to 2017. Section 6 contains a discussion and concluding remarks.

2 A mixed-effects approach for a state-space epidemic model for multiple epidemics

First, we sum up the approach developed in Narci et al. (2021) in the case of single epidemics for prevalence data and extend it to incidence data (Sect. 2.1). By extending this approach, we propose a model for simultaneously considering several epidemics, in the framework of mixed-effects models (Sect. 2.2).

2.1 The basics of the modeling framework for the case of a single epidemic

The epidemic model Consider an epidemic in a closed population of size N with homogeneous mixing, whose dynamics are represented by a stochastic compartmental model with \(d+1\) compartments corresponding to the different health states of the infectious process within the population. These dynamics are described by a density-dependent Markov jump process \({\mathcal {Z}}(t)\) with state space \(\{0,\dots , N\}^d\) and transition rates depending on a multidimensional parameter \(\zeta \). Assuming that \({\mathcal {Z}}(0)/N \rightarrow x_0 \ne (0,\dots ,0)'\), the normalized process \({\mathcal {Z}}(t)/N\) representing the respective proportions of population in each health state converges, as \(N \rightarrow \infty \), to a classical and well-characterized ODE:

$$\begin{aligned} \frac{\partial x}{\partial t}(\zeta ,t)= b( \eta , x(\zeta ,t)); \quad x(0)=x_0, \end{aligned}$$
(1)

where \(\eta =(\zeta ,x_0)\) and \(b(\eta ,\cdot )\) is explicit and easy to derive from the Q-matrix of process \({\mathcal {Z}}(t)\) (see Guy et al. 2015; Narci et al. 2021).

Two stochastic approximations of \({\mathcal {Z}}(t)/N\) are available: a d-dimensional diffusion process \(Z(t_k)\) with drift coefficient \(b(\eta ,\cdot )\) and diffusion matrix \(\frac{1}{N} \Sigma ( \eta ,\cdot )\) (which is also easily deducible from the jump functions of the density-dependent jump process, see e.g. Narci et al. 2021), and a time-dependent Gaussian process \(G_N(t)\) with small variance coefficient (see e.g. Britton and Pardoux 2020), having for expression

$$\begin{aligned} G_N(t)= x(\eta ,t) + \frac{1}{\sqrt{N}} g(\eta ,t), \end{aligned}$$
(2)

where \(g(\eta ,t)\) is a centered Gaussian process with explicit covariance matrix. There is a link between these two processes: let W(t) be a Brownian motion in \({\mathbb {R}}^d\), then \(g(\eta ,t)\) is the centered Gaussian process

$$\begin{aligned} g(\eta ,t) = \int _0^t \Phi (\eta , t,u)\sigma (\eta , x(\eta ,u)) dW(u), \quad \text{ where } \sigma (\eta ,x)\sigma (\eta ,x)^{\prime }= \Sigma (\eta ,x), \end{aligned}$$

and \(\Phi (\eta , t,s) \) is the \(d\times d\) resolvent matrix associated to (1)

$$\begin{aligned} \Phi (\eta , t,s) = \exp \left( \int _{s}^{t} \nabla _x b(\eta ,x(\eta ,u)) \ du\right) , \end{aligned}$$
(3)

with \(\nabla _x b (\eta , x)\) denoting the matrix \(( \frac{\partial b_i}{\partial x_j} (\eta , x))_{1\le i,j\le d}\). In the sequel, we rely on the Gaussian process (2) to represent epidemic dynamics.

Remark 1

This large population framework is valid only in case of a major outbreak. It does not properly describe the beginning and the end of the epidemic outbreak (for this supercritical and subcritical, respectively, branching processes are more appropriate). We expect that this middle part of the epidemic is sufficiently well described by the approximating model to allow parameters estimation. The value \(t_0=0\) does not represent the starting point of the epidemic but the time where the epidemic reaches O(N). Indeed, we just need a time \(t_0\) and a value \(x(t_0)= x_0\) to derive the ODE or the Gaussian process. Moreover, in the inference method developed in the sequel, the value \(x_0\) is unknown and estimated, and for multiple epidemics, a random effect is present for modeling the \((x_{u,0}, u \in U)\) of the U epidemics.

The epidemic is observed at discrete times \(t_0=0< t_1 ,\ldots ,<t_n=T\), where n is the number of observations. Let us assume that the observation times \(t_k\) are regularly spaced, that is \(t_k = k \Delta \) with \(\Delta \) the time step (but the following can be easily adapted to irregularly spaced observation times). Setting \(X_k:= G_N(t_k)\) and \(X_0= x_0\), the model can be written under the auto-regressive AR(1) form

$$\begin{aligned} X_{k} = F_k(\eta ) + A_{k-1} (\eta )X_{k-1} + V_{k}, \quad \text{ with } V_{k} \sim {\mathcal {N}}_d\left( 0, T_k(\eta ,\Delta )\right) \text { and } k\ge 1. \end{aligned}$$
(4)

All the quantities in (4) have explicit expressions with respect to the parameters. Indeed, using (1) and (3), we have

$$\begin{aligned} A_{k-1}(\eta )&= A(\eta ,t_{k-1}) = \Phi (\eta ,t_k, t_{k-1}), \end{aligned}$$
(5)
$$\begin{aligned} F_k(\eta )&= F(\eta ,t_k) = x(\eta ,t_k)- \Phi (\eta ,t_k, t_{k-1})x(\eta ,t_{k-1}), \end{aligned}$$
(6)
$$\begin{aligned} T_k(\eta ,\Delta )&= \frac{1}{N}\int _{t_{k-1}}^{t_k} \Phi (\eta ,t_k,s) \Sigma (\eta ,x(\eta ,s))\; \Phi ^t(\eta ,t_k,s)ds. \end{aligned}$$
(7)

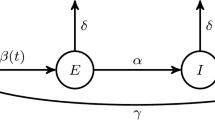
Example: SIR model As an illustrative example, we use the simple SIR epidemic model described in Fig. 1, but other models can be considered (see e.g. the SEIR model, used in Sect. 5).

Fig. 1
figure 1

SIR compartmental model with three blocks corresponding respectively to susceptible (S), infectious (I) and recovered (R) individuals. Transitions of individuals from one health state to another are governed by the transmission rate \(\lambda \) and the recovery rate \(\gamma \), respectively

Full size image

In the SIR model, \(d=2\) and \({\mathcal {Z}}(t)=\left( S(t),I(t)\right) '\). The parameters involved in the transition rates are \(\lambda \) and \(\gamma \) and the initial proportions of susceptible and infectious individuals are \(x_0= (s_0,i_0)'\). Denoting \(\eta =(\lambda ,\gamma ,s_0,i_0)'\), the ODE satisfied by \(x(\eta ,t)= (s(\eta ,t), i(\eta ,t))'\) is

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{\partial s}{\partial t}(\eta ,t)= -\lambda s(\eta ,t) i(\eta ,t); &{}\quad s(\eta ,0)= s_0,\\ \frac{\partial i}{\partial t}(\eta ,t)= \lambda s(\eta ,t) i(\eta ,t)- \gamma i(\eta ,t); &{} \quad i(\eta ,0)= i_0. \end{array}\right. } \end{aligned}$$
(8)

When there is no ambiguity, we denote by s and i the solution of (8). Then, the functions \(b(\eta ,\cdot )\), \(\Sigma (\eta ,\cdot )\) and \(\sigma (\eta ,\cdot )\) are

$$\begin{aligned} b(\eta , s,i) = \begin{pmatrix} - \lambda s i \\ \lambda s i -\gamma i \end{pmatrix}; \quad \Sigma (\eta ,s,i) = \begin{pmatrix} \lambda s i &{} - \lambda s i \\ - \lambda s i &{} \lambda s i + \gamma i \end{pmatrix},\;\sigma (\eta ,s,i) = \begin{pmatrix} \sqrt{\lambda s i} &{} 0 \\ - \sqrt{\lambda s i} &{} \sqrt{\gamma i} \end{pmatrix}. \end{aligned}$$

We refer the reader to Appendix 1 for the computation of \(b(\eta ,\cdot )\), \(\Sigma (\eta ,\cdot )\) and \(\sigma (\eta ,\cdot )\) in the SEIR model. Another parameterization, involving the basic reproduction number \(R_0=\frac{\lambda }{\gamma }\) and the infectious period \(d=\frac{1}{\gamma }\), is more often used for SIR models. Hence, we set \(\eta =(R_0,d,s_0,i_0)'\).

Observation model for prevalence data Following (Narci et al. 2021), we assume that observations are made at times \(t_k=k\Delta , k=1,\dots ,n\), and that some health states are not observed. The dynamics is described by the d-dimensional AR(1) model detailed in (4). Some coordinates are not observed and various sources of noise systematically affect the observed coordinates (measurement errors, observation noises, under-reporting, etc.). This is taken into account by introducing an additional parameter \(\mu \), governing both the levels of noise and the amount of information which is available from the \(q \le d\) observed coordinates, and an operator \(B(\mu ): {\mathbb {R}}^d \rightarrow {\mathbb {R}}^q\). Moreover, we assume that, conditionally on the random variables \((B(\mu )X_k, k=1, \dots ,n)\), these noises are independent but not identically distributed. We approximate their distributions by q-dimensional Gaussian distributions with covariance matrix \(P_k(\eta ,\mu )\) depending on \(\eta \) and \(\mu \). This yields that the observations \((Y_k)\) satisfy

$$\begin{aligned} Y_{k}= B(\mu )X_{k}+W_{k}, \text{ with } W_k \sim {{{\mathcal {N}}}}_q(0,P_k( \eta ,\mu )). \end{aligned}$$
(9)

Let us define a global parameter describing both the epidemic process and the observational process,

$$\begin{aligned} \phi = (\eta ,\mu ). \end{aligned}$$
(10)

Finally, joining (4), (9) and (10) yields the formulation (for both epidemic dynamics and observation process) required to implement Kalman filtering methods in order to estimate the epidemic parameters:

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{k} = F_k(\eta ) + A_{k-1} (\eta )X_{k-1} + V_{k},\; \text{ with } V_{k} \sim {\mathcal {N}}_d\left( 0, T_k(\eta ,\Delta )\right) , \ k\ge 1, \\ Y_{k}= B(\mu )X_{k}+W_{k}, \text{ with } W_{k} \sim {\mathcal {N}}_q\left( 0, P_k(\phi )\right) . \end{array}\right. } \end{aligned}$$
(11)

Example: SIR model (continued) The available observations could be noisy proportions of the number of infectious individuals at discrete times \(t_k\). Denoting by p the reporting rate, one could define the operator \(B(\mu ) = B(p) = (0 \ \ \ p)\) and the covariance error as \(P_k(\phi )=\frac{1}{N}p(1-p)i(\eta ,t_k)\) with \(i(\eta ,t)\) satisfying (8). The expression of \(P_k(\phi )\) mimics the variance that would arise from assuming the observations to be obtained as binomial draws of the infectious individuals.

Observation model for incidence data For this purpose, we have extended the framework developed in Narci et al. (2021). For some compartmental models, the observations (incidence) at times \(t_k\) can be written as the increments of a single or more coordinates, that is \({\tilde{B}}(\mu )(X_{k-1}-X_k)\) where, as above, \({\tilde{B}}(\mu ) : {\mathbb {R}}^d \rightarrow {\mathbb {R}}^q\) is a given operator and \(\mu \) are emission parameters. Let us write the epidemic model in this framework. For \(k=1,\ldots ,n\), let

$$\begin{aligned} \Delta _k X = X_k - X_{k-1}. \end{aligned}$$

From (11), the following holds, denoting by \(I_d\) the \(d \times d\) identity matrix,

$$\begin{aligned} \Delta _k X = F_k(\eta ) + (A_{k-1}(\eta )-I_d) X_{k-1} + V_k. \end{aligned}$$
(12)

As \(X_{k-1} = \sum _{l=1}^{k-1} \Delta _l X + x_0\), (12) becomes:

$$\begin{aligned} \Delta _k X = G_k(\eta ) + (A_{k-1}(\eta )-I_d) \sum _{l=1}^{k-1} \Delta _l X + V_k, \text{ with } \end{aligned}$$
(13)
$$\begin{aligned} G_k(\eta ) = x(\eta ,t_k)-x_0 - \Phi (\eta , t_k, t_{k-1})(x(\eta ,t_{k-1})-x_0). \end{aligned}$$
(14)

To model the errors that affect the data collected \((Y_k)\), we assume that, conditionally on \((\Delta _k X, k=1,\dots ,n)\), the observations are independent and proceed to the same approximation for their distributions

$$\begin{aligned} Y_k = {\tilde{B}}(\mu ) \Delta _k X + {\tilde{W}}_k ; \quad \text{ with } {\tilde{W}}_k \sim {{{\mathcal {N}}}}_q(0, {\tilde{P}}_k(\phi )). \end{aligned}$$
(15)

Consequently, using (13), (14) and (15), the epidemic model for incidence data is adapted as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _k X = G_k(\eta ) + (A_{k-1}(\eta )-I_d) \sum _{l=1}^{k-1} \Delta _l X + V_k, \\ Y_k = {\tilde{B}}(\mu ) \Delta _k X + {\tilde{W}}_k. \end{array}\right. } \end{aligned}$$
(16)

Contrary to (4), \((\Delta _k X, k=1,\dots ,n)\) is not Markovian since it depends on all the past observations. Therefore, it does not possess the required properties of classical Kalman filtering methods. We prove in Appendix 2 that we can propose an iterative procedure and define a new filter to compute recursively the conditional distributions describing the updating and prediction steps together with the marginal distributions of the observations from the model (16).

Example: SIR model (continued) Here, \(\Delta _k X=\left( \frac{\Delta _k S}{N},\frac{\Delta _k I}{N}\right) '\) and the number of new infectious individuals at times \(t_k\) is given by \( \int _{t_{k-1}}^{t_k} \lambda S(t) \frac{I(t)}{N} \ dt = - \Delta _k S\). Observing a proportion p of the new infectious individuals would lead to the operator \({\tilde{B}}(\mu ) = B(p) = (-p \ \ \ 0)\). Mimicking binomial draws, the covariance error could be chosen as \({\tilde{P}}_k(\phi )=\frac{1}{N}p(1-p)(s(\eta ,t_{k-1})-s(\eta ,t_k))\) where \(s(\eta ,t)\) satisfies (8).

2.2 Modeling framework for multiple epidemics

Consider now the situation where a same outbreak occurs in many regions or at different periods simultaneously. We use the index \(1\le u \le U\) to describe the quantities for each unit (e.g. region or period), where U is the total number of units. Following Sect. 2.1, for unit u, the epidemic dynamics are represented by the d-dimensional process \((X_u(t))_{t\ge 0}\) corresponding to \(d+1\) infectious states (or compartments) with state space \(E=[0,1]^d\). It is assumed that \((X_u(t))_{t\ge 0}\) is observed at discrete times \(t_k=k \Delta \) on \([0,T_u]\), \(T_u=n_u \Delta \), where \(\Delta \) is a fixed time step and \(n_u\) is the number of observations, and that \(Y_{u,k}\) are the observations at times \(t_k\). Each of these dynamics has its own epidemic and observation parameters, denoted \(\phi _u\).

To account for intra- and inter-epidemic variability, a two level representation is considered, in the framework of mixed-effects models. First, using the discrete-time Gaussian state-space for prevalence (11) or for incidence data (16), the intra-epidemic variability is described. Second, the inter-epidemic variability is characterized by specifying a set of random parameters for each epidemic.

1. Intra-epidemic variability Let us define \(X_{u,k}:= X_u(t_k)\), \(X_{u,0}= x_{u,0}\) and \(\Delta _k X_u := X_u(t_{k}) - X_u(t_{k-1})\). Using (10), conditionally to \(\phi _u=\varphi \), the epidemic observations for unit u are described as in Sect. 2.1.

For prevalence data, \( 1\le k\le n_u\),

$$\begin{aligned} {\left\{ \begin{array}{ll} X_{u,k}= F_k(\varphi ) + A_{k-1} (\varphi )X_{u,k-1} + V_{u,k},\quad \text{ with } V_{u,k} \sim {\mathcal {N}}_d\left( 0, T_k(\varphi ,\Delta )\right) , \\ Y_{u,k}= B(\varphi )X_{u,k}+W_{u,k}, \quad \text{ with } W_{u,k} \sim {{{\mathcal {N}}}} _q( 0, P_k(\varphi )), \end{array}\right. } \end{aligned}$$
(17)

[see (5), (6) and (7) for the expressions of \(F_k(\cdot )\), \(A_{k-1}(\cdot )\), \(T_k(\cdot ) \) and (9) for \(B(\cdot )\) and \(P_k(\cdot )\)].

For incidence data,

$$\begin{aligned} {\left\{ \begin{array}{ll} \Delta _k X_u = G_k(\varphi ) + (A_{k-1}(\varphi )-I_d) \sum _{l=1}^{k-1} \Delta _l X_u + V_{u,k},\\ Y_{u,k}= {\tilde{B}}(\varphi ) \Delta _k X_u + {\tilde{W}}_{u,k} \quad \text{ with } {\tilde{W}}_{u,k} \sim {{{\mathcal {N}}}} _q( 0, {\tilde{P}}_k(\varphi )), \end{array}\right. } \end{aligned}$$
(18)

[see (14) for the expression of \(G_k(\cdot )\) and (15) for \({\tilde{B}}(\cdot )\) and \({\tilde{P}}_k(\cdot )\)].

2. Inter-epidemic variability

We assume that the epidemic-specific parameters \((\phi _u,1\le u \le U)\) are independent and identically distributed (i.i.d.) random variables with distribution defined as follows,

$$\begin{aligned} {\left\{ \begin{array}{ll} \phi _u = h(\beta ,\xi _u), \\ \xi _u \sim {\mathcal {N}}_c(0,\Gamma ), \end{array}\right. } \end{aligned}$$
(19)

where \(c=\text {dim} \ (\phi _u)\) and \(h(\beta ,x): {\mathbb {R}}^{c} \times {\mathbb {R}}^{c}\rightarrow {\mathbb {R}}^{c}\). The vector \(h(\beta ,x)=\left( h_1(\beta ,x),\ldots ,h_c(\beta ,x)\right) '\) contains known link functions (a classical way to obtain parameterizations easier to handle), \(\beta \in {\mathbb {R}}^{c}\) is a vector of fixed effects and \(\xi _1,\ldots ,\xi _U\) are random effects modeled by U i.i.d centered random variables. The fixed and random effects respectively describe the average general trend shared by all epidemics and the differences between epidemics. Note that it is sometimes possible to propose a more refined description of the inter-epidemic variability by including unit-specific covariates in (19). This is not considered here, without loss of generality.

Remark 2

As far as inference is concerned, there is a compromise to look for between a parsimonious description of the variability between the U epidemics and a more detailed one. The set-up of mixed-effects SDE or Gaussian processes allows to describe simultaneously the stochasticity within and between epidemics. In this framework, epidemics are seen as independent and the presence of structural dependencies between the \((X_u)\) for regional epidemics or the \((\varphi _u)\) for different periods cannot be described in this set-up. This would be conceivable but at the cost of many additional parameters.

Example: SIR model (continued) Let \(s_{0,u} = \frac{S_u(0)}{N_u}\) and \(i_{0,u} = \frac{I_u(0)}{N_u}\) where \(N_u\) is the population size in unit u. The random parameter is \(\phi _u = (R_{0,u},d_u,p_u,s_{0,u},i_{0,u})'\) and has to fulfill the constraints

$$\begin{aligned} R_{0,u}> 1;\; d_u > 0; \; 0< p_u< 1; \; 0< s_{0,u}, i_{0,u} < 1,\; s_{0,u}+i_{0,u} \le 1. \end{aligned}$$

To meet these constraints, one could introduce the following function \(h(\beta ,x): {\mathbb {R}}^{5} \times {\mathbb {R}}^{5}\rightarrow {\mathbb {R}}^{5}\):

$$\begin{aligned} {\left\{ \begin{array}{ll} h_1(\beta ,\xi _u) = \exp \left[ \beta _1+\xi _{1,u}\right] +1, \\ h_2(\beta ,\xi _u) = \exp \left[ \beta _2+\xi _{2,u}\right] , \\ h_3(\beta ,\xi _u) = \frac{1}{1+\exp \left[ -(\beta _3+\xi _{3,u})\right] }, \\ h_4(\beta ,\xi _u) = \frac{1}{1+\exp \left[ -(\beta _4+\xi _{4,u})\right] +\exp \left[ -(\beta _5+\xi _{5,u})\right] }, \\ h_5(\beta ,\xi _u) = \frac{\exp \left[ -(\beta _4+\xi _{4,u})\right] }{1+\exp \left[ -(\beta _4+\xi _{4,u})\right] +\exp \left[ -(\beta _5+\xi _{5,u})\right] }, \end{array}\right. } \end{aligned}$$
(20)

where \(\xi _u \sim _{i.i.d.} {\mathcal {N}}_5(0,\Gamma )\) and \(\phi _u= h(\beta ,\xi _u)\).

In this example, we supposed that all the parameters have both fixed and random effects, but it is also possible to consider a combination of random-effect parameters and purely fixed-effect parameters (see Sect. 4.1 for instance).

3 Parametric inference

To estimate the model parameters \(\theta =(\beta ,\Gamma )\), with \(\beta \) and \(\Gamma \) defined in (19), containing the parameters modeling the intra- and inter-epidemic variability, we develop an algorithm in the spirit of Delattre and Lavielle (2013) allowing to derive the maximum likelihood estimator (MLE).

3.1 Maximum likelihood estimation

The model introduced in Sect. 2.2 can be seen as a latent variable model with \({\mathbf {y}} = (y_{u,k}, 1 \le u \le U, 0\le k \le n_u)\) the observed data and \(\varvec{\Phi } = (\phi _u,1\le u \le U)\) the latent variables. Denote respectively by \(p({\mathbf {y}};\theta \)), \(p(\varvec{\Phi };\theta )\) and \(p({\mathbf {y}}|\varvec{\Phi };\theta )\) the probability density of the observed data, of the random effects and of the observed data given the unobserved ones. By independence of the U epidemics, the likelihood of the observations \({\mathbf {y}}_u=(y_{u,1},\ldots ,y_{u,n_u})\) is given by:

$$\begin{aligned} p({\mathbf {y}};\theta ) = \prod _{u=1}^{U} p({\mathbf {y}}_u;\theta ). \end{aligned}$$

Computing the distribution \(p({\mathbf {y}}_u;\theta )\) of the observations for any epidemic u requires the integration of the conditional density of the data given the unknown random effects \(\phi _u\) with respect to the density of the random parameters:

$$\begin{aligned} p({\mathbf {y}}_u;\theta ) = \int p({\mathbf {y}}_u|{\phi }_u;\theta ) p({\phi }_u;\theta ) \ d{\phi }_u. \end{aligned}$$
(21)

Due to the non-linear structure of the proposed model, the integral in (21) is not explicit. Moreover, the computation of \(p({\mathbf {y}}_u|{\phi }_u;\theta )\) is not straightforward due to the presence of latent states in the model. Therefore, the inference algorithm needs to account for these specific features.

Let us first deal with the integration with respect to the unobserved random variables \({\phi }_u\). In latent variable models, the use of the EM algorithm (Dempster et al. 1977) allows to compute iteratively the MLE. Iteration k of the EM algorithm combines two steps: (1) the computation of the conditional expectation of the complete log-likelihood given the observed data and the current parameter estimate \(\theta _k\), denoted \({\mathcal {Q}}(\theta |\theta _k)\) (E-step); (2) the update of the parameter estimates by maximization of \({\mathcal {Q}}(\theta |\theta _k)\) (M-step). In our case, the E-step cannot be performed because \({\mathcal {Q}}(\theta |\theta _k)\) does not have a simple analytic expression. We rather implement a Stochastic Approximation-EM (SAEM, Delyon et al. 1999) which combines at each iteration the simulation of unobserved data under the conditional distribution given the observations (S-step) and a stochastic approximation of \({\mathcal {Q}}(\theta |\theta _k)\) (SA-step).

  1. (a)

    General description of the SAEM algorithm Given some initial value \(\theta _{0}\), iteration m of the SAEM algorithm consists in the three following steps:

    • (S-step) Simulate a realization of the random parameters \(\varvec{\Phi }_m\) under the conditional distribution given the observations for a current parameter \(\theta _{m-1}\) denoted \(p(\cdot |{\mathbf {y}};\theta _{m-1})\).

    • (SA-step) Update \({\mathcal {Q}}_m(\theta )\) according to

      $$\begin{aligned} {\mathcal {Q}}_m(\theta ) = {\mathcal {Q}}_{m-1}(\theta ) + \alpha _m(\log p({\mathbf {y}},\varvec{\Phi }_m;\theta ) - {\mathcal {Q}}_{m-1}(\theta )), \end{aligned}$$

      where \((\alpha _m)_{m \ge 1}\) is a sequence of positive step-sizes s.t. \(\sum _{m=1}^{\infty } \alpha _m = \infty \) and \(\sum _{m=1}^{\infty } \alpha _m^2 < \infty \).

    • (M-step) Update the parameter estimate by maximizing \({\mathcal {Q}}_m(\theta )\)

      $$\begin{aligned} \theta _m = \text {arg max}_{\theta } \ {\mathcal {Q}}_m(\theta ). \end{aligned}$$

In our case, an exact sampling under \(p(\cdot |{\mathbf {y}};\theta _{m-1})\) in the S-step is not feasible. In such intractable cases, MCMC algorithms such as Metropolis-Hastings algorithm can be used (Kuhn and Lavielle 2004).

  1. (b)

    Computation of the S-step by combining the Metropolis-Hastings algorithm with Kalman filtering techniques

In the sequel, we combine the S-step of the SAEM algorithm with a MCMC procedure.

For a given parameter value \(\theta \), a single iteration of the Metropolis–Hastings algorithm consists in:

  1. (1)

    Generate a candidate \(\varvec{\Phi }^{(c)} \sim q(\cdot |\varvec{\Phi }_{m-1},{\mathbf {y}};\theta )\) for a given proposal distribution q

  2. (2)

    Take

    $$\begin{aligned} \varvec{\Phi }_{m} = {\left\{ \begin{array}{ll} \varvec{\Phi }_{m-1} \text { with probability } 1 - \rho (\varvec{\Phi }_{m-1},\varvec{\Phi }^{(c)}),\\ \varvec{\Phi }^{(c)} \text { with probability } \rho (\varvec{\Phi }_{m-1},\varvec{\Phi }^{(c)}), \end{array}\right. } \end{aligned}$$

    where

    $$\begin{aligned} \rho (\varvec{\Phi }_{m-1},\varvec{\Phi }^{(c)}) = \text {min}\left[ 1, \frac{p({\mathbf {y}}|\varvec{\Phi }^{(c)}; \theta ) \ p(\varvec{\Phi }^{(c)}; \theta ) \ q(\varvec{\Phi }_{m-1}|\varvec{\Phi }^{(c)},{\mathbf {y}}; \theta )}{p({\mathbf {y}}|\varvec{\Phi }_{m-1}; \theta ) \ p(\varvec{\Phi }_{m-1}; \theta ) \ q(\varvec{\Phi }^{(c)}|\varvec{\Phi }_{m-1},{\mathbf {y}}; \theta )}\right] .\nonumber \\ \end{aligned}$$
    (22)

To compute the rate of acceptation of the Metropolis-Hastings algorithm in (22), we need to calculate

$$\begin{aligned} p({\mathbf {y}}_u|{\phi }_u;\theta ) = p(y_{u,0}|\phi _u;\theta ) \prod _{k=1}^{n_u} p(y_{u,k}|y_{u,0},\ldots ,y_{u,k-1},{\phi }_u;\theta ), \ 1 \le u \le U. \end{aligned}$$

Let \(y_{u,k:0}:=(y_{u,0},\ldots ,y_{u,k})\), \(k\ge 1\). In both models (17) and (18), the conditional densities \(p(y_{u,k}|y_{u,k-1:0},{\phi }_u;\theta )\) are Gaussian densities. In model (17) involving prevalence data, their means and variances can be exactly computed with Kalman filtering techniques (see Narci et al. 2021). In model (18), the Kalman filter can not be used in its standard form. We therefore develop an alternative filtering algorithm.

From now on, we omit the dependence in u and \(\varvec{\Phi }\) for sake of simplicity.

Prevalence data

Let us consider model (11) and recall the successive steps of the filtering developed in Narci et al. (2021). Assume that \(X_0 \sim {{{\mathcal {N}}}}_d(x_0, T_0)\) and set \({{\hat{X}}}_0= x_0,{{\hat{\Xi }}}_0= T_0\). Then, the Kalman filter consists in recursively computing for \(k\ge 1\):

  1. 1.

    Prediction: \({\mathcal {L}}(X_{k+1}|Y_k,\ldots ,Y_1) = {\mathcal {N}}_d(\widehat{X}_{k+1},\widehat{\Xi }_{k+1})\)

    $$\begin{aligned} \widehat{X}_{k+1}&= F_{k+1} + A_k {\overline{X}}_k \\ \widehat{\Xi }_{k+1}&= A_k {\overline{T}}_k A_k' + T_{k+1} \end{aligned}$$
  2. 2.

    Updating: \({\mathcal {L}}(X_k|Y_k,\ldots ,Y_1) = {\mathcal {N}}_d({\overline{X}}_k,{\overline{T}}_k)\)

    $$\begin{aligned} \overline{X_k}&= \widehat{X}_k + \widehat{\Xi }_k B' (B \widehat{\Xi }_k B' + P_k)^{-1}(Y_k - B\widehat{X}_k) \\ \overline{T_k}&= \widehat{\Xi }_k - \widehat{\Xi }_k B' (B \widehat{\Xi }_k B' + P_k)^{-1} B \widehat{\Xi }_k \end{aligned}$$
  3. 3.

    Marginal: \({\mathcal {L}}(Y_{k+1}|Y_k,\ldots ,Y_1) = {\mathcal {N}}(\widehat{M}_{k+1},\widehat{\Omega }_{k+1})\)

    $$\begin{aligned} \widehat{M}_{k+1}&= B \widehat{X}_{k+1} \\ \widehat{\Omega }_{k+1}&= B \widehat{\Xi }_{k+1} B' + P_{k+1} \end{aligned}$$

Incidence data Let us consider model (16). Assume that \({\mathcal {L}}(\Delta _1 X) = {\mathcal {N}}_d(G_1,T_1)\) and \({\mathcal {L}}(Y_1 | \Delta _1 X) = {\mathcal {N}}_q({\tilde{B}}\Delta _1 X, {\tilde{P}}_1)\). Let \(\widehat{\Delta _1 X} = G_1 = x(t_1) - x_0\) and \(\widehat{\Xi }_1 = T_1\). Then, at iterations \(k\ge 1\), the filtering steps are:

  1. 1.

    Prediction: \({\mathcal {L}}(\Delta _{k+1} X|Y_k,\ldots ,Y_1) = {\mathcal {N}}_d(\widehat{\Delta _{k+1} X},\widehat{\Xi }_{k+1})\)

    $$\begin{aligned} \widehat{\Delta _{k+1} X}&= G_{k+1} + (A_k-I_d) \left( \sum _{l=1}^{k}\overline{\Delta _l X}\right) \\ \widehat{\Xi }_{k+1}&= (A_k-I_d) \left( \sum _{l=1}^{k}{\overline{T}}_l\right) (A_k-I_d)' + T_{k+1} \end{aligned}$$
  2. 2.

    Updating: \({\mathcal {L}}(\Delta _k X|Y_k,\ldots ,Y_1) = {\mathcal {N}}_d(\overline{\Delta _k X},{\overline{T}}_k)\)

    $$\begin{aligned} \overline{\Delta _k X}&= \widehat{\Delta _k X} + \widehat{\Xi }_k {\tilde{B}}' ({\tilde{B}} \widehat{\Xi }_k {\tilde{B}}' + {\tilde{P}}_k)^{-1}(Y_k - {\tilde{B}}\widehat{\Delta _k X}) \\ {\overline{T}}_k&= \widehat{\Xi }_k - \widehat{\Xi }_k {\tilde{B}}' ({\tilde{B}} \widehat{\Xi }_k {\tilde{B}}' + {\tilde{P}}_k)^{-1} {\tilde{B}} \widehat{\Xi }_k \end{aligned}$$
  3. 3.

    Marginal: \({\mathcal {L}}(Y_{k+1}|Y_k,\ldots ,Y_1) = {\mathcal {N}}(\widehat{M}_{k+1},\widehat{\Omega }_{k+1})\)

    $$\begin{aligned} \widehat{M}_{k+1}&= {\tilde{B}} \widehat{\Delta _{k+1} X} \\ \widehat{\Omega }_{k+1}&= {\tilde{B}} \widehat{\Xi }_{k+1} {\tilde{B}}' + {\tilde{P}}_{k+1} \end{aligned}$$

The equations are deduced in Appendix 2, the difficult point lying in the prediction step, i.e. the derivation of the conditional distribution \({{{\mathcal {L}}}}( \Delta _{k+1} X|Y_{k},\ldots , Y_1) \).

3.2 Convergence of the SAEM-MCMC algorithm

Generic assumptions guaranteeing the convergence of the SAEM-MCMC algorithm were stated in Kuhn and Lavielle (2004). These assumptions mainly concern the regularity of the model [see assumptions (M1–M5)] and the properties of the MCMC procedure used in step S (SAEM3’). Under these assumptions, and providing that the step sizes \((\alpha _m)\) are such that \(\sum _{m=1}^{\infty } \alpha _m = \infty \) and \(\sum _{m=1}^{\infty } \alpha _m^2 < \infty \), then the sequence \((\theta _m)\) obtained through the iterations of the SAEM-MCMC algorithm converges almost surely toward a stationary point of the observed likelihood.

Let us remark that by specifying the inter-epidemic variability through the modeling framework of Sect. 2.2, our approach for multiple epidemics fulfills the exponentiality condition stated in (M1) provided that all the components of \(\phi _u\) are random. Hence the algorithm proposed above converges almost surely toward a stationary point of the observed likelihood under the standard regularity conditions stated in (M2-M5) and assumption (SAEM3’).

There is no theoretical guarantee that the algorithm converges to a global maximum of the likelihood. It is a classical problem in statistics which concerns the majority of algorithms developed to optimize non convex functions. In practice, to prevent convergence of the algorithm to a local maximum of the likelihood, it is possible to consider different starting values for the parameters and to finally choose the set of estimated values associated with the highest likelihood value among the ones obtained with these different starting points. Nevertheless, depending on the complexity of the model and the number of observations to process, the computation time of the algorithm for a given set of starting values can be important. Therefore, the strategy adopted in the paper is to use a simulated annealing version of SAEM in order to have more flexibility in the first iterations and thus to escape more easily from potential local maxima of the likelihood at the beginning of the algorithm [cf. Appendix 3, 5th item and pages 249–252 in Lavielle (2014)]. This does not completely prevent from converging to a local optimum but we can reasonably hope to reach the global optimum by considering fewer different initializations than with a standard version of the algorithm. In practice, the a priori knowledge of specialists in the field of study, in this case epidemiologists, can help to initialize the algorithm close to the optimum.

4 Assessment of parameter estimators performances on simulated data

First, the performances of our inference method are assessed on simulated stochastic SIR dynamics. Second, the estimation results are compared with those obtained by an empirical two-step approach.

For a given population of size N and given parameter values, we use the Gillespie algorithm (Gillespie 1977) to simulate a two-dimensional Markov jump process \({{{\mathcal {Z}}}}(t)= (S(t),I(t))'\). Then, choosing a sampling interval \(\Delta \) and a reporting rate p, we consider prevalence data \((O(t_k), k=1,\ldots ,n)\) simulated as binomial trials from a single coordinate of the system \(I(t_k)\). We refer the reader to Appendix 5 for an assessment of the performances of our inference method on simulated incidence data.

4.1 Simulation setting

Model Recall that the epidemic-specific parameters are \(\phi _u = \left( R_{0,u}, d_u, p_u,s_{0,u},i_{0,u}\right) '\). In the sequel, for all \(u\in \{1,\ldots ,U\}\), we assume that \(R_{0,u}>1\) and \(0<p_u<1\) are random parameters. We also set \(s_{0,u} + i_{0,u} = 1\) (which means that the initial number of recovered individuals is zero), with \(0<i_{0,u}<1\) being a random parameter. Moreover, we consider that the infectious period \(d_u = d>0\) is a fixed parameter since the duration of the infectious period can reasonably be assumed constant between different epidemics. It is important to note that the case study is outside the scope of the exponential model since a fixed parameter has been included. We refer the reader to Appendix 3 for implementation details.

Four fixed effects \(\beta \in {{\mathbb {R}}}^4\) and three random effects \(\xi _u=(\xi _{1,u},\xi _{3,u},\xi _{4,u})' \sim {{\mathcal {N}}}_3 (0,\Gamma )\) are considered. Therefore, using (19) and (20), we assume the following model for the fixed and random parameters:

$$\begin{aligned} \phi _u=\left( R_{0,u},d_u,p_u,i_{0,u}\right) ' = h(\beta ,\xi _u), \quad \text{ with } \end{aligned}$$
(23)
$$\begin{aligned} h_1(\beta ,\xi _u)&= \exp \left[ \beta _1+\xi _{1,u}\right] +1,\\ h_2(\beta ,\xi _u)&= \exp \left[ \beta _2\right] , \\ h_i(\beta ,\xi _u)&= \frac{1}{1+\exp \left[ -(\beta _i+\xi _{i,u})\right] }, \ i=3,4. \end{aligned}$$

In other words, random effects on \((R_0,p,i_0)\) and fixed effect on d are considered. Moreover, these random effects come from a priori independent sources, so that there is no reason to consider correlations between \(\xi _{1,u}\), \(\xi _{3,u}\) and \(\xi _{4,u}\), and we can assume in this set-up a diagonal form for the covariance matrix \(\Gamma = \text{ diag } \Gamma _{i}\), \(i\in \{1,3,4\}\).

Parameter values

We consider two settings (denoted respectively (i) and (ii) below) corresponding to two levels of inter-epidemic variability (resp. high and moderate). The fixed effects values \(\beta \) are chosen such that the intrinsic stochasticity of the epidemic dynamics is significant (a second set of fixed effects values leading to a lower intrinsic stochasticity is also considered; see Appendix 4 for details).

  • Setting (i): \(\beta =(-0.81,0.92,1.45,-2.20)'\) and \(\Gamma =\text {diag}(0.47^2,1.50^2,0.75^2)\) corresponding to \({\mathbb {E}}\left( R_{0,u}\right) = 1.5\), \(CV_{R_{0,u}} = 17 \%\); \(d=2.5\); \({\mathbb {E}}\left( p_{u}\right) \approx 0.74\), \(CV_{p_u} \approx 31 \%\); \({\mathbb {E}}\left( i_{0,u}\right) \approx 0.12\), \(CV_{i_{0,u}} \approx 66 \%\);

  • Setting (ii): \(\beta =(-0.72,0.92,1.45,-2.20)'\) and \(\Gamma =\text {diag}(0.25^2,0.90^2,0.50^2)\) corresponding to \({\mathbb {E}}\left( R_{0,u}\right) = 1.5\), \(CV_{R_{0,u}} = 8 \%\); \(d=2.5\); \({\mathbb {E}}\left( p_{u}\right) \approx 0.78\), \(CV_{p_u} \approx 18 \%\); \({\mathbb {E}}\left( i_{0,u}\right) \approx 0.11\), \(CV_{i_0} \approx 45 \%\);

where \(CV_{\phi }\) stands for the coefficient of variation of a random variable \(\phi \). Let us note that the link between \(\phi _u\) and \((\beta ,\xi _u)\) for p and \(i_0\) does not have an explicit expression.

Data simulation The population size is fixed to \(N_u=N=10{,}000\). For each \(U\in \{20,50,100\}\), \(J=100\) data sets, each composed of U SIR epidemic trajectories, are simulated. Independent samplings of \(\left( \phi _{u,j}=\left( R_{0,u},d_u,p_u,i_{0,u}\right) _j'\right) \), \(u=1,\dots U\), \(j=1,\ldots ,J\), are first drawn according to model (23). Then, conditionally to each parameter set \(\phi _{u,j}\), a bidimensionnal Markov jump process \({\mathcal {Z}}_{u,j}(t) = (S_{u,j}(t),I_{u,j}(t))'\) is simulated. Normalizing \({\mathcal {Z}}_{u,j}(t)\) with respect to \(N_u\) and extracting the values of the normalized process at regular time points \(t_k = k \Delta \), \(k=1,\ldots ,n_{u,j}\), gives the \(X_{u,k,j}=\left( \frac{S_{u,k,j}}{N_u},\frac{I_{u,k,j}}{N_u}\right) '\)’s. A fixed discretization time step is used, i.e. the same value of \(\Delta \) is used to simulate all the epidemic data. For each epidemic, \(T_{u,j}\) is defined as the first time point at which the number of infected individuals becomes zero. Two values of \(\Delta \) are considered (\(\Delta \in \{0.425,2\}\)) corresponding to an average number of time-point observations \({\overline{n}}_j = \frac{1}{U}\sum _{u=1}^{U} n_{u,j} \in \{20,100\}\). Only trajectories that did not exhibit early extinction were considered for inference. The theoretical proportion of these trajectories is given by \(1-(1 / R_0)^{I_0}\) (Andersson and Britton 2000). Then, given the simulated \(X_{u,k,j}\)’s and parameters \(\phi _{u,j}\)’s, the observations \(Y_{u,k,j}\) are generated from binomial distributions \({\mathcal {B}}(I_{u,k,j},p_{u,j})\).

4.2 Point estimates and standard deviations for inferred parameters

Tables 1 and 2 show the estimates of the expectation and standard deviation of the mixed effects \(\phi _{u}\), computed from the estimations of \(\beta \) and \(\Gamma \) using functions h defined in (23), for settings (i) and (ii). For each parameter, the reported values are the mean of the \(J=100\) parameter estimates \(\phi _{u,j}\), \(j\in \{1,\ldots ,J\}\), and their standard deviations in brackets.

Remark 3

Via the link functions h, the random parameters \(\Phi _u\) can be expressed as a function of the fixed effects \(\beta \) and the random effects \(\xi _u\). When the link has a suitable form (for example, a log link function), it is possible to explicitly obtain the mean and variance of the \(\Phi _u\)’s. When it is not the case (for example, with a logit link function), we can compute the empirical mean and variance based on simulations of the \(\Phi _u\)’s. For more complex link functions (such as the logit link function), this is no longer true and the empirical mean and variance are computed via simulations of the \(\Phi _u\)’s. This is the method used here.

Table 1 Estimates for setting (i): high inter-epidemic variability
Full size table
Table 2 Estimates for setting (ii): moderate inter-epidemic variability
Full size table

The results show that all the point estimates are close to the true values (relatively small bias), whatever the inter-epidemic variability setting, even for small values of \({\bar{n}}\) and U. When the number of epidemics U increases, the standard error of the estimates decreases, but it does not seem to have a real impact on the estimation bias. Besides, observations of higher frequency of the epidemics (large \({\bar{n}}\)) lead to lower bias and standard deviations. It is particularly marked concerning both expectation and standard deviations of the random parameters \(R_{0,u}\) and \(p_{u}\). Irrespective to the level of inter-epidemic variability, the estimations are quite satisfactory. While standard deviations of \(R_{0,u}\) are slightly over-estimated, even for large U and \({\overline{n}}\), this trend in bias does not affect the standard deviations of \(p_{u}\) and \(i_{0,u}\).

For a given data set, Fig. 2 displays convergence graphs of the SAEM algorithm for each estimates of model parameters in setting (i) with \(U=100\) and \({\bar{n}}=100\). Although the model does not belong to the curved exponential family, convergence of model parameters towards their true value is obtained for all parameters.

Fig. 2
figure 2

Convergence graphs of the SAEM algorithm for estimates of \(\beta =(\beta _1,\beta _2,\beta _3,\beta _4)\) and \(\text {diag}(\Gamma )=(\Gamma _1,\Gamma _3,\Gamma _4)\). Setting (i) with \(U=100\) and \({\bar{n}}=100\). Parameter values at each iteration of the SAEM algorithm (plain blue line) and true values of model parameters (dotted red line) (color figure online)

Full size image

4.3 Comparison with an empirical two-step approach

The inference proposed method (referred to as SAEM-KM) is compared to an empirical two-step approach not taking into account explicitly mixed effects in the model. For that purpose, let us consider the method presented in Narci et al. (2021) (referred to as KM) performed in two steps: first, we compute the estimates \(\hat{\phi }_u\) independently on each of the U trajectories. Second, the empirical mean and variance of the \(\hat{\phi }_{u}\)’s are computed. We refer the reader to Appendix 3 for practical considerations on implementation of the KM method.

Let us consider \({\bar{n}}=50\) and \(U\in \{20,100\}\). Figure 3 displays the distribution of the bias of the parameter estimates \(\phi _{u,j}\), \(j\in \{1,\ldots ,J\}\), \(J=100\), obtained with SAEM-KM and KM for simulation settings (i) and (ii).

Fig. 3
figure 3

Boxplots (25th, 50th and 75th percentiles) of the bias of the estimates of each model parameter, with \({\bar{n}}=50\), obtained with SAEM-KM (blue boxes) and KM (red boxes). Two levels: \(U=20\) and \(U=100\) epidemics. Dark colours: high inter-epidemic variability [setting (i)]. Light colours: moderate inter-epidemic variability [setting (ii)]. The symbol represents the estimated mean bias. For sake of clarity, we removed extreme values from the graphical representation. This concerns only the parameter \(R_0\) and the KM method: 37 values for \({\mathbb {E}}(R_{0,u})\) (35 in setting (i), 2 in setting (ii)) and 50 values for \(\text {sd}(R_{0,u})\) (47 in setting (i), 3 in setting (ii)) (color figure online)

Full size image

We notice a clear advantage to consider the mixed-effects structure. Overall, the results show that SAEM-KM outperforms KM. This is more pronounced for standard deviation estimates in the large inter-epidemic variability setting (i) than in the moderate inter-epidemic variability setting (ii). Concerning the expectation estimates, their dispersion around the median is lower for KM than for SAEM-KM, especially in setting (ii), but the bias of KM estimates is also higher. When the inter-epidemic variability is high (setting (i)), the performances of the two inference methods are substantially different. In particular, KM sometimes fails to provide plausible estimates (especially for parameter \(R_0\)).

We also tested other values for \({\bar{n}}\) and N (not shown here), e.g. \({\bar{n}}=20\) (lower amount of information) and \(N=2000\) (higher intrinsic variability of epidemics). In such cases, KM also failed to provide satisfying estimations whereas the mixed-effects approach was much more robust.

5 Case study: influenza outbreaks in France

Data The SAEM-KM method is evaluated on a real data set of influenza outbreaks in France provided by the Réseau Sentinelles (url: www.sentiweb.fr). We use the daily number of influenza-like illness (ILI) cases between 1990 and 2017, considered as a good proxy of the number of new infectious individuals. The daily incidence rate was expressed per 100,000 inhabitants. To select epidemic periods, we chose the arbitrary threshold of weekly incidence of 160 cases per 100,000 inhabitants (Cauchemez et al. 2008), leading to 28 epidemic dynamics. Two epidemics have been discarded due to their bimodality (1991–1992 and 1998). Therefore, \(U=26\) epidemic dynamics are considered for inference.

Compartmental model Let us consider the SEIR model (see Fig. 4). An individual is considered exposed (E) when infected but not infectious. Denote \(\eta =(\lambda ,\epsilon ,\gamma ,x_0)\), with \(x_0=(s_0,e_0,i_0,r_0)\), the parameters involved in the transition rates, where \(\epsilon \) is the transition rate from E to I. ODEs of the SEIR model are as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{ds}{dt}(\eta ,t) = - \lambda s(\eta ,t) i(\eta ,t), \\ \frac{de}{dt}(\eta ,t) = \lambda s(\eta ,t) i(\eta ,t) - \epsilon e(\eta ,t), \\ \frac{di}{dt}(\eta ,t) = \epsilon e(\eta ,t) -\gamma i(\eta ,t), \\ \frac{dr}{dt}(\eta ,t) = \gamma i(\eta ,t), \\ x_0 = (s_0,e_0,i_0,r_0). \end{array}\right. } \end{aligned}$$
(24)
Fig. 4
figure 4

SEIR compartmental model with four blocks corresponding respectively to susceptible (S), exposed (E), infectious (I) and recovered (R) individuals. Transitions of individuals from one health state to another are governed by the transmission rate \(\lambda \), the incubation rate \(\epsilon \) and the recovery rate \(\gamma \)

Full size image

Another parametrization exhibits the basic reproduction number \(R_0=\frac{\lambda }{\gamma }\), the incubation period \(d_E=\frac{1}{\epsilon }\) and the infectious period \(d_I=\frac{1}{\gamma }\). Thus, the epidemic parameters are \(\eta =(R_0,d_E,d_I,s_0,e_0,i_0)'\). Let us describe the two-layer model used in the sequel.

Intra-epidemic variability For each epidemic u, let \(X_u=\left( \frac{S_u}{N_u},\frac{E_u}{N_u},\frac{I_u}{N_u}\right) '\) and

$$\begin{aligned} \eta _u = \left( R_{0,u},d_{E,u},d_{I,u},s_{u,0},e_{u,0},i_{u,0}\right) , \end{aligned}$$

where the population size is fixed at \(N_u = N = 100{,}000\). Denote by \(\text {Inc}_u(t_k)\) the number of newly infected individuals at time \(t_k\) for epidemic u. We have

$$\begin{aligned} \text {Inc}_u(t_k)= \int _{t_{k-1}}^{t_k} \frac{1}{d_{E,u}} E_u(t) dt=S_u(t_{k-1}) - S_u(t_k) + E_u(t_{k-1}) - E_u(t_k)= - (\Delta _k S_u+\Delta _k E_u). \end{aligned}$$

Observations are modeled as incidence data observed with Gaussian noises. We draw our inspiration from Bretó (2018) to account for over-dispersion in data. Therefore, assuming a reporting rate \(p_u\) for epidemic u, the mean and the variance of the observed newly infected individuals are respectively defined as \(p_u \text {Inc}_u(t_k)\) and \(p_u \text {Inc}_u(t_k) + \tau _u^2 p_u^2 \text {Inc}_u(t_k)^2\), where parameter \(\tau _u\) is introduced to handle over-dispersion in the data. Denote \(\phi _u = \left( \eta _u,p_u,\tau _u^2\right) \). Therefore, we use the model defined in (18) with \(\Delta _k X_u = \left( \frac{\Delta _k S_u}{N},\frac{\Delta _k E_u}{N},\frac{\Delta _k I_u}{N}\right) '\), \(V_{u,k} \sim {\mathcal {N}}_d\left( 0, T_k(\phi _u,\Delta )\right) \), \({\tilde{W}}_{u,k} \sim {{{\mathcal {N}}}} _q( 0, {\tilde{P}}_k(\phi _u))\), \(G_k(\cdot )\), \(A_{k-1}(\cdot )\) and \(T_k(\cdot )\) deriving from (26) in Appendix 1, \({\tilde{B}}(\phi _u) = (-p_u \ \ -p_u \ \ 0)\) and

$$\begin{aligned} {\tilde{P}}_k(\phi _u) = \frac{1}{N}{\tilde{B}}(\phi _u) \Delta _k x_u + \tau _u^2 \left( {\tilde{B}}(\phi _u) \Delta _k x_u\right) ^2, \end{aligned}$$

where \(x(\cdot ,t)\) is the ODE solution of (24).

Inter-epidemic variability In this real data study, due to identifiability issues, we have to perform inference by fixing parameters \(d_E\) (incubation period), \(d_I\) (infectious period) and \(r_0\) (initial proportion of removed individuals). Let us first comment on the two parameters \(d_E\), \(d_I\). Studies in the literature found discrepant values of these durations (see Cori et al. 2012 for a review), varying from 0.64 (Fraser et al. 2009) to 3.0 (Pourbohloul et al. 2009) days for the incubation period and from 1.27 (Fraser et al. 2009) to 8.0 (Pourbohloul et al. 2009) days for the infectious period. For example, Cori et al. (2012) estimated that \(d_E=1.6\) and \(d_I=1.0\) days on average using excretion profiles from experimental infections. In two other papers, these durations were fixed according to previous studies (e.g. Mills et al. 2004; Ferguson et al. 2005): \((d_E,d_I) = (1.9,4.1)\) days (Chowell et al. 2008); \((d_E,d_I) = (0.8,1.8)\) days (Baguelin et al. 2013). Performing a systematic review procedure from viral shedding and/or symptoms, Carrat et al. (2008) estimated \(d_E\) to be between 1.7 and 2.0 on average. Therefore in what follows, we consider the latent and infectious periods \(d_E\) and \(d_I\) known and test three combinations of values: \((d_E,d_I) = (1.6,1.0)\), (0.8, 1.8) and (1.9, 4.1).

We consider that the basic reproduction number \(R_0\) and the reporting rate p are random, reflecting the assumptions that the transmission rate of the pathogen varies from season to season and the reporting could change over the years. Moreover, we assume \(e_u(0)=i_u(0)\) random and unknown (i.e. the proportion of initial exposed and infectious individuals is variable between epidemics). Cauchemez et al. (2008) assumed that at the start of each influenza season, a fixed average of \(27\%\) of the population is immune, that is \(r_{0,u}=r_0=0.27\). To assess the robustness of the model with respect to the \(r_0\) value, we test three values: \(r_0 \in \{0.1,0.27,0.5\}\). This leads to \(s_{0,u} = 1 - r_0 - 2 i_{0,u}\) random and unknown. Finally, we assume that \(\tau _u^2=\tau ^2\) is fixed and unknown. Thus, we have to study nine candidate models with: known parameters \((d_E,d_I)\in \{(0.8,1.8),(1.6,1.0),(1.9,4.1)\}\) and \(r_0\in \{0.1,0.27,0.5\}\); fixed and unknown parameter \(\tau ^2\) ; random and unknown parameters \(R_0\), \(i_{0}\) and p.

Therefore, using (19), we consider the following model for random parameters:

$$\begin{aligned} \phi _u=\left( R_{0,u},p_u,i_{0,u},\tau ^2\right) ' = h(\beta ,\xi _u), \quad \text{ with } \end{aligned}$$
(25)
$$\begin{aligned} h_1(\beta ,\xi _u)&= \exp \left[ \beta _1+\xi _{1,u}\right] +1,\\ h_j(\beta ,\xi _u)&= \frac{1}{1+\exp \left[ -(\beta _j+\xi _{j,u})\right] }, \ j=2,3, \\ h_4(\beta ,\xi _u)&= \exp \left[ \beta _4\right] , \end{aligned}$$

where fixed effects \(\beta \in {\mathbb {R}}^4\) and the random effects are \(\xi _u \sim _{i.i.d.} {\mathcal {N}}_3(0,\Gamma )\) with \(\Gamma \) a covariance matrix assumed to be diagonal.

Parameter estimates These nine candidate models correspond to different combinations of values of \(((d_E,d_I),r_0)\). They have exactly the same structure and the same complexity in terms of number of parameters to be estimated. After the inference is performed for each of these nine candidate models, we have to choose the best candidate values. Using importance sampling techniques, we estimate the observed log-likelihood of each model from the estimated parameters values initially obtained with the SAEM algorithm. Table 3 provides the estimated log-likelihood values of the nine models of interest. Irrespectively of the \(r_0\) value, we find that the model with \((d_E,d_I)=(1.9,4.1)\) outperforms the two other models in terms of log-likelihood value. Moreover, for a given combination of values of \((d_E,d_I)\), the estimated log-likelihood values are quite similar according to the three \(r_0\) tested values.

Table 3 Estimated values of the observed log-likelihood of the model obtained by testing nine combinations of values of \(((d_E,d_I),r_0)\)
Full size table

Remark 4

Model comparison is usually performed by using information criteria like BIC which are defined by adding a penalty term, depending on the total number of model parameters, to \(-2 \times \) the log-likelihood. The best model according to these criteria is the model that leads to the smallest criterion value. We could have used BIC to compare the nine candidate models, but as they have the same number of parameters, the penalty is useless and the comparison is fully based on the \(-2 \times \) log-likelihood term of the criterion. That is why we only show the estimated log-likelihood values in Table 3. Instead of comparing values of \(-2 \times \) log-likelihood, we directly compare log-likelihood values, so higher values are better.

Let us focus on the model with \((d_E,d_I)=(1.9,4.1)\). Table 4 presents the estimation results of the model parameters obtained by testing the three values of \(r_0\): 0.1, 0.27 and 0.5.

Table 4 Estimates of the mean, 5th and 95th percentiles and coefficient of variation (CV) for model parameters \(\left( R_{0,u},i_{0,u},p_u,\tau ^2\right) '\), assuming \((d_E,d_I)=(1.9,4.1)\) and testing three values of \(r_0\): 0.1, 0.27 and 0.5
Full size table

The average estimated value of \(R_0\) is quite contrasted according to the \(r_0\) value: between 1.81 and 3.28 from \(r_0=0.1\) to \(r_0=0.5\). By comparison, in Cauchemez et al. (2008), \(R_0\) is estimated to be 1.7 during school term, and 1.4 in holidays, using a population structured into households and schools. Chowell et al. (2008) estimated a different reproduction number \({\tilde{R}}=(1-r_0)R_0=1.3\), measuring the transmissibility at the beginning of an epidemic in a partially immune population, from mortality data. In our case, the average value of \({\tilde{R}}\) is estimated to 1.63, 1.63 and 1.64 when \(r_0=0.1\), 0.27 and 0.5 respectively. Therefore, given the nature of the observations (new infected individuals) and the considered model, this appears to be difficult to correctly identify \(R_0\) together with \(r_0\). Indeed, the fraction of immunized individuals at the beginning of each seasonal influenza epidemic is an important parameter for the epidemic dynamics, but its value is not well known. This has implications for the stability of the estimation of the other parameters. Interestingly, the average reporting rate is estimated particularly low (around \(10 \%\) irrespective of the \(r_0\) value). Moreover, we observe that \(R_0\) together with p and \(i_0\) seem to be variable from season to season, with moderate coefficient of variation \(\text {CV}(R_{0,u})\) close to \(15\%\) and high coefficients of variation \(\text {CV}(p_{u})\) and \(\text {CV}(i_{0,u})\) around \(50 \%\) and \(70 \%\) respectively.

It is possible to perform a maximum a posteriori (MAP) estimation of the parameters \(\phi _u\) corresponding to each period, by computing \(\hat{\phi }_u = \mathrm {argmax}_{\phi _u} p(\phi _u|Y_u;\hat{\theta })\) where \(\hat{\theta }\) is the parameter estimate obtained with the SAEM algorithm. We refer the reader to Appendix 6 for a graphical representation of the time-series behaviour of \(R_{0,u}\) and \(p_u\), which could be interesting from an epidemiological point of view.

Fig. 5
figure 5

Post-predictive check. Observations (number of ILI as proxy for new infectious for each of the U epidemics) (blue). Simulated trajectories obtained for \(r_0=0.1\) (red), \(r_0=0.27\) (magenta) and \(r_0=0.5\) (green) in three steps: (i) generation of 1000 \(\hat{\phi }_u\) values based on estimated values of parameters; (ii) given \(\hat{\phi }_u\), simulation of 1000 epidemics according to the model (18); (iii) computation of average trajectory (solid line) and 5th and 95th percentiles (dotted lines) of the 1000 simulated epidemics. Population size fixed to \(N=100{,}000\) (color figure online)

Full size image

The post-predictive check is shown in Fig. 5. The difference between the average simulated curves obtained with estimated parameter values is negligible according to the \(r_0\) value. Considering the values of \({\tilde{R}}\), very close in the three scenarios, the proximity of the predicted trajectories is not surprising. Let us emphasize that the majority of the observations are within the predicted envelope (5th and 95th percentiles). Moreover, the predicted average trajectory informs about generic trends of influenza outbreaks: on average, the epidemic peak should be reached around 25 days after the beginning of the outbreak with an incidence of 90/100, 000 inhabitants approximately.

Remark 5

We observe on Fig. 5 that the two epidemics lasting longer, corresponding to the seasons 1998–1999 and 2012–2013, tend to be above the 95% percentile near the end, which could be explained by the fact that they grow very slowly the first three weeks. Also, considering a different threshold defining the epidemic season (here taken equal to 160 cases per 100,000 inhabitants) could change the data-points considered for these two trajectories and hence their positioning with respect to the average or confidence bound trajectories. Finally, the predicted envelope of the 5th and 95th percentiles is ensured to contain, by construction, only \(90 \%\) of observations. Therefore, some observations can be found below the 5th percentile or above the 95th percentile.

6 Discussion

In this paper, we propose a generic inference method taking into account simultaneously in a unique model multiple epidemic trajectories and providing estimations of key parameters from incomplete and noisy epidemic data (prevalence or incidence). The framework of the mixed-effects models was used to describe the inter-epidemic variability, whereas the intra-epidemic variability was modeled by an autoregressive Gaussian process. The Gaussian formulation of the epidemic model for prevalence data used in Narci et al. (2021) was extended to the case where incidence data were considered. Then, the SAEM algorithm was coupled with Kalman-like filtering techniques in order to estimate model parameters.

The performances of the estimators were investigated on simulated data of SIR dynamics, under various scenarios, with respect to the parameter values of epidemic and observation processes, the number of epidemics (U), the average number of observations for each of the U epidemics (\({\bar{n}}\)) and the population size (N). The results show that all estimates are close to the true values (reasonable biases), whatever the inter-epidemic variability setting, even for small values of \({\bar{n}}\) and U. The performances, in term of precision, are improved when increasing U, whereas the bias and standard deviations of the estimations decrease when increasing \({\bar{n}}\). We also compared our method with a two-step empirical approach that processes the different data sets separately and combines the individual parameter estimates a posteriori to provide an estimate of inter-epidemic variability (Narci et al. 2021). When the number of observations is too low and/or the coefficient of variation of the random effects is high, SAEM-KM clearly outperforms KM.

The proposed inference method was also evaluated on an influenza data set provided by the Réseau Sentinelles, consisting in the daily number of new infectious individuals per 100,000 inhabitants between 1990 and 2017 in France, using a SEIR compartmental model. Testing different combinations of values for \((d_E,d_I)\) and \(r_0\), we find that \((d_E,d_I)=(1.9,4.1)\) leads to the best fitting model. Then, irrespective to the \(r_0\) value, we estimated an average value of \({\tilde{R}}=(1-r_0)R_0\) to be around 1.6. Moreover, we highlighted a non-negligible variability from season to season that is quantitatively assessed. This variability appears especially in the initial conditions (\(i_0\)) and the reporting rate (p), as a combined effect of observational uncertainties and differences between seasons. Although to a lesser extent, \(R_0\) also appears to vary between seasons, plausibly reflecting the variability in the transmission rate (\(\lambda \)). Obviously, the estimations can strongly depend on the choice of the compartmental model, the nature and frequency of the observations and the distribution of the random parameters. Our contribution is to propose a finer estimation of the model parameters by taking into account simultaneously all the influenza outbreaks in France for the inference procedure. This leads to an explicit and rigorous estimation of the seasonal variability.

Other methods have been implemented to deal with multiple epidemic dynamics. Bretó et al. (2020) proposed a likelihood-based inference methods for panel data modeled by non-linear partially observed jump processes incorporating unit-specific parameters and shared parameters. Nevertheless, the framework of mixed-effects models was not really investigated. Prague et al. (2020) used an ODE system with mixed effects on the parameters to analyse the first epidemic wave of Covid-19 in various regions in France by inferring key parameters from the daily incidence of infectious ascertained and hospitalized infectious cases. To our knowledge, there are no published studies aiming at the estimation of key parameters simultaneously from several outbreak time series using both a stochastic modeling of epidemic processes and random effects on model parameters.

The main advantage of our method is to propose a direct access to the inter-epidemic variability between multiple outbreaks. Taking into account simultaneously several epidemics in a unique model leads to an improvement of statistical inference compared with empirical methods which consider independently epidemic trajectories. For example, we can mention two experimental settings: (1) the number of epidemics is high but the number of observations per epidemic is low; (2) the number of observations per epidemic is high but the number of epidemics is low. In such cases, mixed-effects approaches can provide more satisfying estimation results. This benefit more than compensates for the careful calibration of the tuning parameters of the SAEM algorithm.

This paper focuses of independent epidemics. Even in this apparently simple case, a non negligible number of technical and methodological difficulties arise. Given these difficulties and as this setting is rarely suitable in practice, there is a compromise to find for inference, between a parsimonious description of the U epidemics and a more detailed one. The set-up of mixed-effects SDE allows to describe simultaneously the within and between epidemic stochasticity. This study can be considered as the first investigation step of the multiple epidemics data set, that does not prevent a second investigation step with a more accurate description including for instance some shared parameters, unit specific parameters, a dependence structure, etc. Extensions of this work would imply modifications of the model but also important modifications of the algorithm, the latter being necessarily specific to the way the dependence is accounted for. A first strategy could be to incorporate a given dependence structure between the \(X_u\)’s directly in the time series equations by specifying the \(X_{u,k}\)’s about this way: \(X_{u,k}=g_{\eta }(X_{1,k-1}, X_{2,k-1}, \ldots , X_{U,k-1}, V_k)\), where \(g_{\eta }(\cdot )\) is known up to parameter \(\eta \). This mechanically increases the number of parameters in \(\eta \), which may lead to high computation times when U is large. A second strategy should be to introduce a correlation between the \(\phi _u\)’s by defining the epidemic-specific parameters as \(\Phi = \begin{pmatrix} \phi _1 \\ \phi _2 \\ \vdots \\ \phi _U \end{pmatrix} \sim {\mathcal {N}}_{c \times U} (0,\Omega )\) with \(\Omega \) a non block diagonal covariance matrix of size \(c \times U\). Here again, the number of parameters to be estimated can be increased significantly depending on the way the dependency is parametrized. In both cases, the simulation step of the algorithm has to be modified because the random effects can no longer be simulated independently. The modifications of the algorithm implied by these two ways of modeling the dependence between epidemics require an important additional work and are thus not considered in this paper.

In some practical cases in epidemiology, it might be difficult to determine whether a parameter is fixed or random. Consequently, our approach could be associated with model selection techniques to inform this choice, using a criterion based on the log-likelihood of observations [see for instance Delattre et al. (2014) and Delattre and Poursat (2020)]. This would allow to determine more precisely which parameters reflect inter-individual variability and thus help to better understand the mechanisms underlying this variability. Moreover, we presented a case study on influenza outbreaks, where the variability between epidemics is seasonal, but our approach can be also applied on epidemics spreading simultaneously in many regions. In this case, the inter-epidemic variability is spatial and it would be interesting to evaluate trends from one region to another.