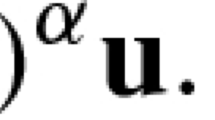Abstract
In this paper, we deal with the existence of global mild solutions and asymptotic behavior to the viscous Camassa–Holm equation in the locally uniform spaces. First we establish the global well-posedness for the Cauchy problem of viscous Camassa–Holm equation in \({\mathbb {R}}^1\) for any initial data \(u_0\in {\dot{H}}^1_U({\mathbb {R}}^1).\) Then we study the long time dynamical behavior of non-autonomous viscous Camassa–Holm equation on \({\mathbb {R}}^1\) with a new class of external forces and show the existence of \((H^1_U({\mathbb {R}}^1),H^1_\phi ({\mathbb {R}}^1))\)-uniform(w.r.t. \(g\in \mathcal {H}_{L^2_U({\mathbb {R}}^1)}(g_0)\)) attractor \(\mathcal {A}_{\mathcal {H}_{L^2_U({\mathbb {R}}^1)}(g_0)}\) with locally uniform external forces being translation uniform bounded but not translation compact in \(L_b^2({\mathbb {R}};L^2_U({\mathbb {R}}^1))\).
Similar content being viewed by others
References
Amann, H.: Nonhomogeneous linear and quasilinear elliptic and parabolic boundary value problems. In: Function Spaces, Differential Operators and Nonlinear Analysis. Teubner-Texte Math., vol. 133. Teubner, Stuttgart, pp. 9–126 (1993)
Arrieta, J., Cholewa, J., Dlotko, T., Rodriguez-Bernal, A.: Linear parabolic equations in locally uniform spaces. Math. Models Methods Appl. Sci. 14, 253–293 (2004)
Arrieta, J., Cholewa, J., Dlotko, T., Rodriguez-Bernal, A.: Asymptotic behavior and attractors for reaction diffusion equations in unbounded domain. Nonlinear Anal. 56, 515–554 (2004)
Arrieta, J., Moya, N., Rodriguez-Bernal, A.: Asymptotic behavior of reaction diffusion equations in weighted Sobolev spaces, Submitted (2009)
Babin, A., Vishik, M.: Attractors of partial differential evolution equations in an unbounded domain. Proc. R. Soc. Edinb. Sect. A 116, 221–243 (1990)
Bortolan, M.C., Carvalho, A.N., Langa, J.A.: Structure of attractors for skew product semiflows. J. Differ. Equ. 257(2), 490–522 (2014)
Bressan, A., Constantin, A.: Global conservative solutions of the Camassa–Holm equation. Arch. Ration. Mech. Anal. 183(2), 215–239 (2007)
Camassa, R., Holm, L.: An integrable shallow-water equation with peaked solitons. Phys. Rev. Lett. 71, 1661–1664 (1993)
Carvalho, A.N., Dlotko, T.: Partly dissipative systems in locally uniform spaces. Colloq. Math. 100, 221–242 (2004)
Carvalho, A.N., Langa, J.A., Robinson, J.C.: Attractors for Infinite-dimensional Non-autonomous Dynamical Systems. Applied Mathematical Sciences, vol. 182. Springer, Berlin (2012)
Chepyzhov, V., Vishik, M.: Attractors for Equations of Mathematical Physics, vol. 49. American Mathematical Society, New York (2002)
Chepyzhov, V., Vishik, M.: Attractors of nonautonomous dynamical systems and their dimension. J. Math. Pures Appl. 73, 279–333 (1994)
Cholewa, J.W., Dlotko, T.: Cauchy problems in weighted Lebesgue spaces. Czechoslov. Math. J. 54, 991–1013 (2004)
Cholewa, J.W., Dlotko, T.: Global Attractors in Abstract Parabolic Problems. Cambridge University Press, Cambridge (2000)
Constantin, A., Escher, J.: Global existence and blow-up for a shallow water equation. Ann. Sc. Norm. Sup. Pisa 26, 303–328 (1998)
Danchin, R.: A note on well-posedness for Camassa–Holm equation. J. Differ. Equ. 192(2), 429–444 (2003)
Escher, J., Yin, Z.: Initial boundary value problems of the Camassa–Holm equation. Commun. Partial Differ. Equ. 33, 377–395 (2008)
Fokas, A.S., Fuchssteiner, B.: Symplectic structures, their Bäcklund transformation and hereditary symmetries. Physica D. 4, 47–66 (1981)
Gui, G., Liu, Y., Olver, J., Qu, C.: Wave-breaking and Peakons for a modified Camassa–Holm equation. Commun. Math. Phys. 319, 731–759 (2013)
Hale, J.: Asymptotic Behavior of Dissipative Systems. Amer. Math. Soc, Providence, RI (1988)
Haraux, A.: Systemes Dynamiques Dissipatifs et Applications. Masson, Paris (1991)
Henry, D.: Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Mathematics, vol. 840. Springer, Berlin (1981)
Kato, T.: The Cauchy problem for quasi-linear symmetric hyperbolic systems. Arch. Ration. Mech. Anal. 58, 181–205 (1975)
Kouranbaeva, : The Camassa–Holm equation as geodesic flow on the diffeomorphism group. J. Math. Phys. 40, 857–868 (1999)
Lu, S., Wu, H., Zhong, C.: Attractors for nonautonomous 2D Navier–Stokes equations with normal external forces. Discret. Contin. Dyn. Syst. 13, 701–719 (2005)
McKean, H.P.: Breakdown of the Camassa–Holm equation. Commun. Pure Appl. Math. 57(3), 416–418 (2004)
Mielke, A., Schneider, G.: Attractors for modulation equations on unbounded domainsexistence and comparison. Nonlinearity 8(5), 743–768 (1995)
Moise, I., Rosa, R., Wang, X.: Attractors for noncompact nonautonomous systems via energy equations. Discret. Cont. Dyn. Syst. 10(1), 473–496 (2004)
Molinet, Luc: On well-posedness results for Camassa–Holm equation on the line: a survey. J. Nonlinear Math. Phys. 11(4), 521–533 (2004)
Stanislavova, M., Stefanov, A.: On global finite energy solutions of the Camassa–Holm equation. J. Fourier Anal. Appl. 11(5), 511–531 (2005)
Stanislavova, M., Stefanov, A.: Attractors for the viscous Camassa–Holm equation. Discret. Contin. Dyn. Syst. Ser. A 18(1), 159–186 (2007)
Xin, Z., Zhang, P.: On the weak solutions to a shallow water equation. Commun. Pure Appl. Math. 53(11), 1411–1433 (2000)
Xin, Z., Zhang, P.: On the uniqueness and large time behavior of the weak solutions to a shallow water equation. Commun. Partial Differ. Equ. 27(9–10), 1815–1844 (2002)
Yang, M., Sun, C.: Dynamics of strongly damped wave equations in locally uniform spaces: attractors and asymptotic regularity. Trans. Am. Math. Soc. 361, 1069–1101 (2009)
Yin, Z.: Well-posedness, global solutions and blowup phenomena for a nonlinearly dispersive wave equation. J. Evol. Equ. 4, 391–419 (2004)
Yin, Z.: On the blow-up scenario for the generalized Camassa–Holm equation. Commun. Partial Differ. Equ. 29, 867–877 (2004)
Yue, G.C., Zhong, C.K.: Dynamics of non-autonomous reaction-diffusion equations in locally uniform spaces. Topol. Methods Nonlinear Anal. 46, 935–965 (2015)
Yue, G.C., Zhong, C.K.: Global attractors for the Gray–Scott equations in locally uniform spaces. Discret. Contin. Dyn. Syst. B 21, 337–356 (2016)
Yue, G.C.: Attractors for non-autonomous reaction-diffusion equations with fractional diffusion in locally uniform spaces. Discret. Contin. Dyn. Syst. B 22, 1645–1671 (2017)
Zelik, S.: The attractor for a nonlinear hyperbolic equation in the unbounded domain. Discret. Contin. Dyn. Syst. 7, 593–641 (2001)
Zhong, C.K., Yang, M.H., Sun, C.Y.: The existence of global attractors for the norm-to-weak continuous semigroup and application to the nonlinear reaction–diffusion equations. J. Differ. Equ. 223, 367–399 (2006)
Acknowledgements
The author would like to thank the anonymous referee for the careful reading of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
The author is supported by NSF of China under Grant 11501289.
Appendix: Some Properties of Uniform Normal External Forces
Appendix: Some Properties of Uniform Normal External Forces
In this section we present some result concerning the locally uniform spaces \(L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) with \(1<p\) and \(1<q<N.\) Recall that a function \(\sigma (s)\in L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) is said to be translation compact(tr.c.) if the closure of \(\{\sigma (s+h)|h\in {\mathbb {R}}\}\) is compact in \(L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N)).\) The set of all tr.c. functions in \(L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) is denoted by \(L_c^p({\mathbb {R}};L^q_U({\mathbb {R}}^N)).\)
We first recall two propositions [11] that gives the compactness criterion in \(L^p(t_1,t_2;L^q_U({\mathbb {R}}^N)).\)
Proposition A.1
A set \(\Sigma \subset L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) is precompact in \(L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) if and only if the set \(\Sigma |_\Omega \) is precompact in \(L^p_{loc}({\mathbb {R}};L^q(\Omega ))\) for every bounded subset \(\Omega \subset {\mathbb {R}}^N.\) Here \(\Sigma |_{\Omega }\) denotes the restriction of the set \(\Sigma \) to the subset \(\Omega .\)
According to the definition of translation compact function in \(L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) and this proposition, a function \(g\in L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) is tr.c. if and only if
The following proposition gives a compactness criterion in \(L_{loc}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N)),\) whose proof is essentially given in Proposition 3.2 of [11].
Proposition A.2
Let \(\Omega \subset {\mathbb {R}}^N\) be a bounded domain. Then a function \(\psi (s)\) is tr.c. in \(L_{loc}^p({\mathbb {R}};L^q(\Omega ))\) if and only if
-
(i)
for any fixed \(h\in {\mathbb {R}}\) the set \(\big \{\int _t^{t+h}\psi (s)ds|t\in {\mathbb {R}}\big \}\) is precompact in \(L^q(\Omega );\)
-
(ii)
there exists a positive function \(\xi (s)\) with \(\xi (s)\rightarrow 0^+\) as \(s\rightarrow 0^+\) such that
$$\begin{aligned} \int _t^{t+1} \Vert \psi (s)-\psi (s+l)\Vert ^p_{L^q(\Omega )}ds\le \xi (|l|)\quad \text {for all}\;\;t\in {\mathbb {R}}. \end{aligned}$$(A.1)
The following relationship between tr.c. function space \(L_c^p({\mathbb {R}};L^q_U({\mathbb {R}}^N)),\) uniform normal function space \(L_{un}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) and \(L_b^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) has been essentially established for the bounded domain of \({\mathbb {R}}^N\) in [25]. According to Propositions A.1, A.2 and the definition of topology of these spaces, we can prove the following conclusion by using the method of [25]. Hence, we omit details here.
Theorem A.3
Let \(p,q\ge 1,\) then
-
(i)
\(L_c^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) is a closed subspace of \(L_b^p({\mathbb {R}};L^q_U({\mathbb {R}}^N));\)
-
(ii)
\(L_c^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\subset L_{un}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N));\)
-
(iii)
\(L_{un}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) is a closed subspace of \(L_b^p({\mathbb {R}};L^q_U({\mathbb {R}}^N)).\)
In particular, if the external force g(x, t) is given by \(g(x,t)=m(t)n(x),\) \(n(x)\in L^q_U({\mathbb {R}}^N),\) and let \(m(t)\in L^p_{loc}({\mathbb {R}})\) be the uniform normal, i.e., \(\sup \limits _{t\in {\mathbb {R}}}\int _t^{t+\eta }\Vert m(s)\Vert ^pds\le \varepsilon ,\) then
Now, we will give some examples to explain the inclusion relationship of these spaces given by Theorem A.3.
Example A.4
For \(k_1,k_2=1,2,\ldots ,\) we take
and
it follows that
On the other hand, for any \(\eta >0\) there exist \(k_2\) such that \(\frac{1}{k_2}\le \eta ,\) set \(t=k_2,\) then
which implies g(x, t) belonging to \(L_b^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) but not \(L_{un}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N)).\)
Example A.5
For \(k_1,k_2=1,2,\ldots ,\) we take
and
it yields
Thus, for any \(0<\varepsilon <\frac{1}{2^{\frac{1}{p-1}}},\) let \(\eta =\varepsilon ^{\frac{p}{p-1}},\) and we have
However, it is easy to see that for any \(\frac{1}{k_2^p}\le l<\frac{1}{k_2}-\frac{1}{k_2^p}\) satisfying \(k_2>2^{\frac{1}{p-1}},\)
which implies from Proposition A.2 that \(g(x,t)=m(t)n(x)\) dose not belong to \(L_c^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\) but in \(L_{un}^p({\mathbb {R}};L^q_U({\mathbb {R}}^N))\).
Rights and permissions
About this article
Cite this article
Yue, G. The Attractors of Camassa–Holm Equation in Unbounded Domains. Appl Math Optim 83, 2211–2240 (2021). https://doi.org/10.1007/s00245-019-09624-8
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00245-019-09624-8