Long-Time Behavior for a Class of Semi-linear Viscoelastic Kirchhoff Beams/Plates

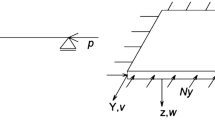
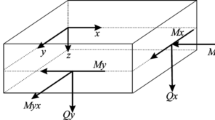
Abstract

This is a complementation work of the paper referred in Jorge Silva, Muñoz Rivera and Racke (Appl Math Optim 73:165–194, 2016) where the authors proposed a semi-linear viscoelastic Kirchhoff plate model. While in [28] it is presented a study on well-posedness and energy decay rates in a historyless memory context, here our main goal is to consider the problem in a past history framework and then analyze its long-time behavior through the corresponding autonomous dynamical system. More specifically, our results are concerned with the existence of finite dimensional attractors as well as their intrinsic properties from the dynamical systems viewpoint. In addition, we also present a physical justification of the model under consideration. Hence, our new achievements complement those established in [28] to the case of memory in a history space setting and extend the results in Jorge Silva and Ma (IMA J Appl Math 78:1130–1146, 2013, J Math Phys 54:021505, 2013) to the case of dissipation only given by the memory term.

Appendix: Examples for F

We finish this work by giving some examples of $C^1$-vector fields $F:\mathbb {R}^n\rightarrow \mathbb {R}^n$ satisfying Assumption $\mathbf {(A2)}$, or else, more generally that:

(a):

There exist positive constants $k_1,\ldots ,k_n$ and $q_1,\ldots ,q_n$ such that

$$\begin{aligned} |\nabla F_j(z)|\le k_j(1+|z|^{q_j}), \quad \forall \quad z\in \mathbb {R}^n, \quad \forall \quad j=1,\ldots ,n. \end{aligned}$$

(A.1)

(b):

$F=\nabla f$ with $f:\mathbb {R}^n\rightarrow \mathbb {R}$ so that

$$\begin{aligned} -a_0-a_1|z|^{2}\le f(z)\le F(z) z + a_2|z|^{2}, \quad \forall \; z\in \mathbb {R}^n, \end{aligned}$$

(A.2)

for some nonnegative constants $a_0,a_1,a_3\ge 0.$

We remark that it is important to consider at least one example such that (A.2) holds true with $a_0>0$, by differing of the examples presented in [28, Sect. 4.2]. For the sake of completeness, we also provide an example where $a_0=0.$ Also, since condition (A.1) is only technical, we shall omit comments on it in the next examples.

Example A.1

(Example 4.11 in [28]) Let us first consider

$$\begin{aligned} F(z)=|z|^{q}z, \ \ F=\nabla f \ \ \text{ with } \ \ f(z)=\frac{1}{q+2}|z|^{q+2}, \quad q\ge 0. \end{aligned}$$

Then, condition (A.2) is readily verified for any $a_1,a_2\ge 0$ and $a_0=0$. In this case, the vector field generates the p-Laplacian operator

$$\begin{aligned} \text{ div }F(\nabla u) \, = \, \text{ div }\left( |\nabla u|^{q} \nabla u\right) , \end{aligned}$$

with power $p=2q+1$ that must satisfy condition (3.5).

Example A.2

(Example 4.12 in [28]) Let $F=\nabla f$ be a conservative vector field, where

$$\begin{aligned} f(z)=\frac{\kappa }{q+2}|z|^{q+2}+\tau z, \end{aligned}$$

with $q\ge 0,$$\kappa >0,$ and $\tau =(\tau _1,\ldots ,\tau _n)\in \mathbb {R}^n.$ Thus, condition (A.2) is fulfilled with $a_0= \frac{|\tau |^2}{2}$, $a_1=\frac{1}{2}$, and any $a_2\ge 0$.

Example A.3

Let us take $F(z)=|z|^{q}z-\lambda |z|^{r}z, \, q>r>0, \lambda >0.$ Then, $F=\nabla f$, where

$$\begin{aligned} f(z)=\frac{1}{q+2}|z|^{q+2}-\frac{\lambda }{r+2}|z|^{r+2}. \end{aligned}$$

Let us verify (A.2). We first check that there exist $a_0, a_1 \ge 0$ such that

$$\begin{aligned} - a_0 - a_1 |z|^2 \le f(z), \quad \forall \, z \in \mathbb {R}^n. \end{aligned}$$

In fact, for a fixed $a_1 \ge 0$, it is enough to choose $a_0 \ge 0$ such that

$$\begin{aligned} a_0 \ge - \min _{t \ge 0}\left\{ \frac{t^{q+2}}{q+2} - \frac{\lambda t^{r+2}}{r+2} + a_1t^2 \right\} . \end{aligned}$$

To the second inequality in (A.2), it is enough to choose $a_2 \ge 0$ such that

$$\begin{aligned} a_2 \ge \max _{t \ge 0}\left\{ \left( \frac{1}{q+2} - 1\right) t^q - \lambda \left( \frac{1}{r+2} - 1\right) t^r\right\} . \end{aligned}$$

Note that since $(\frac{1}{q+2} - 1)< 0$ and $r < q$, such maximum there exists. In this case, the vector field generates the q, r-Laplacian operator provided in the elliptic problem (5.9).