A new parameter free partially penalized immersed finite element and the optimal convergence analysis

Abstract

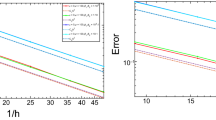
This paper presents a new parameter free partially penalized immersed finite element method and convergence analysis for solving second order elliptic interface problems. A lifting operator is introduced on interface edges to ensure the coercivity of the method without requiring an ad-hoc stabilization parameter. The optimal approximation capabilities of the immersed finite element space is proved via a novel new approach that is much simpler than that in the literature. A new trace inequality which is necessary to prove the optimal convergence of immersed finite element methods is established on interface elements. Optimal error estimates are derived rigorously with the constant independent of the interface location relative to the mesh. The new method and analysis have also been extended to variable coefficients and three-dimensional problems. Numerical examples are also provided to confirm the theoretical analysis and efficiency of the new method.

Appendices

Appendix A: Technical results for the 2D cases

1.1 Proof of Lemma 1

Proof

$:$ Note that when T is an isosceles right triangle, the proof can be found in the literature, see for example [18, 43]. We now provide the proof for $\alpha _{max}\le \pi /2$. Given a function $\phi \in S_h(T)$, if we known the jump $c_1:=(\nabla \phi ^+-\nabla \phi ^-)\cdot \mathbf {n}_h$ which is a constant, then the function $\phi$ can be written as

$$\begin{aligned} \phi =I_{h,T}\phi +c_1(w-I_{h,T}w), \end{aligned}$$

(A.1)

with

$$\begin{aligned} w(x)=\left\{ \begin{aligned}&w^+(x)=d_{\varGamma _{h,T}^{ext}}(x)~~&\text{ in } T_h^+,\\&w^-(x)=0&\text{ in } T_h^-, \end{aligned}\right. ~~~~ d_{\varGamma _{h,T}^{ext}}(x)=\left\{ \begin{aligned}&\mathrm{dist}(x,\varGamma _{h,T}^{ext})~~&\text{ if } x\in T_h^+,\\&-\mathrm{dist}(x,\varGamma _{h,T}^{ext})&\text{ if } x\in T_h^-, \end{aligned}\right. \nonumber \\ \end{aligned}$$

(A.2)

where $I_{h,T}$ is the standard linear nodal interpolation operator on $T, \varGamma _{h,T}^{ext}$ is a straight line containing $\varGamma _h\cap T$, and $\mathrm{dist}(x, \varGamma _{h,T}^{ext})$ is the distance between x and $\varGamma _{h,T}^{ext}$. Substituting (A.1) into the third identity in (2.4), we obtain the following equation for $c_1$,

$$\begin{aligned} (1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h)c_1=(\beta ^-/\beta ^+-1)\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}. \end{aligned}$$

(A.3)

Clearly, if we can prove

$$\begin{aligned} 0\le \nabla I_{h,T}w\cdot \mathbf {n}_h\le 1, \end{aligned}$$

(A.4)

then

$$\begin{aligned} (1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h)\ge \left\{ \begin{aligned}&1\qquad&\text{ if } \beta ^-/\beta ^+\ge 1,\\&\beta ^-/\beta ^+\qquad&\text{ if } 0<\beta ^-/\beta ^+<1, \end{aligned}\right. \end{aligned}$$

(A.5)

which implies that the equation (A.3) has a unique solution. Substituting the solution of (A.3) into (A.1) yields

$$\begin{aligned} \phi =I_{h,T}\phi +\frac{(\beta ^-/\beta ^+-1)\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}}{1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h}(w-I_{h,T}w), \end{aligned}$$

(A.6)

which proves the lemma.

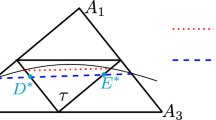
Next, we prove (A.4). There are two cases. Case $\mathrm I$: $\triangle A_2DE=T_h^+$ (see Fig. 4a) and Case $\mathrm II$: $\triangle A_2DE=T_h^-$. In Case $\mathrm I$, since $w(A_1)=w(A_3)=0$, it holds

$$\begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h=\nabla \lambda _2\cdot \mathbf{n }_hd_{\varGamma _{h,T}^{ext}}(A_2)=\nabla \lambda _2\cdot \mathbf{n }_h|A_2A_{2,\perp }|=1-\lambda _2(A_{2,\perp }),\qquad \end{aligned}$$

(A.7)

where $A_{2,\perp }$ is the orthogonal projection of the point $A_2$ onto the line DE, and $\lambda _i(x)$ is the standard linear basis function defined by $\lambda _i(A_j)=\delta _{ij}$ (the Kronecker symbol). The polynomial extension of $\lambda _i(x)$ is also denoted by $\lambda _i(x)$ for simplicity of notations. In Case II ($\triangle A_2DE=T_h^-$), for the sake of clarity, we replace the notations $w, \mathbf {n}_h$ and $d_{\varGamma _{h,T}^{ext}}$ by $\tilde{w}$, $\tilde{\mathbf {n}}_h$ and $\tilde{d}_{\varGamma _{h,T}^{ext}}$, respectively. Obviously, $\tilde{\mathbf {n}}_h=-\mathbf {n}_h$ and $\tilde{d}_{\varGamma _{h,T}^{ext}}(A_2)=-|A_2A_{2,\perp }|$. Similar to (A.7), we have

$$\begin{aligned} \nabla I_{h,T}\tilde{w}\cdot \tilde{\mathbf {n}}_h=1-\lambda _1(A_{1,\perp })+1-\lambda _3(A_{3,\perp }). \end{aligned}$$

(A.8)

However, using the signed distance function $\tilde{d}_{\varGamma _{h,T}^{ext}}$ we also have

$$\begin{aligned} \nabla I_{h,T}\tilde{w}\cdot \tilde{\mathbf {n}}_h= & {} \nabla (\sum _{i=1,3}\tilde{d}_{\varGamma _{h,T}^{ext}}(A_i)\lambda _i)\cdot \tilde{\mathbf{n }}_h=\nabla (\tilde{d}_{\varGamma _{h,T}^{ext}}-\tilde{d}_{\varGamma _{h,T}^{ext}}(A_2)\lambda _2)\cdot \tilde{\mathbf {n}}_h\nonumber \\= & {} 1-\nabla \lambda _2\cdot \mathbf{n }_h|A_2A_{2,\perp }|=1-\nabla I_{h,T}w\cdot \mathbf {n}_h. \end{aligned}$$

(A.9)

Thus, it suffices to consider Case $\mathrm I$: $\triangle A_2DE=T_h^+$ which is shown in Fig. 4a.

If $A_2$ and $A_{2,\perp }$ are on different sides of the line $A_1A_3$ (see Fig. 4b for an illustration), then we have $\angle A_1A_3A_2>\angle A_3QA_2>\frac{\pi }{2}$. This contradicts the condition $\alpha _{max}\le \frac{\pi }{2}$. Thus, we conclude that $A_2$ and $A_{2,\perp }$ are on the same side of the line $A_1A_3$, which together with the fact $\lambda _2(A_2)=1$, $\lambda _2(A_1)=\lambda _2(A_3)=0$, leads to

$$\begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h=1-\lambda _2(A_{2,\perp })\le 1, \end{aligned}$$

On the other hand, using the condition $\angle A_2A_3A_1$ and $\angle A_2A_1A_3\le \alpha _{max}\le \frac{\pi }{2}$, we conclude $\overrightarrow{A_1A_3}\cdot \mathbf{t }_h>0$, which implies

$$\begin{aligned} \begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h&=\nabla \lambda _2\cdot \mathbf{n }_h|A_2A_{2,\perp }|=|A_2A_{2,\perp }||\nabla \lambda _2|\mathbf{n }_{A_1A_3}\cdot \mathbf{n }_h\\&=|A_2A_{2,\perp }||\nabla \lambda _2||A_1A_3|^{-1}\overrightarrow{A_1A_3}\cdot \mathbf{t }_h\ge 0, \end{aligned} \end{aligned}$$

where $\mathbf{n }_{A_1A_3}$ is the unit normal vector of the line $A_1A_3$ pointing toward $A_2$. $\square$

A counter example for $\alpha _{max}>\frac{\pi }{2}$:

$$\begin{aligned} \begin{aligned}&A_1=(0,0),~~ A_2=(-\sqrt{3},1),~~ A_3=(1,0),~~ D=(0,0),\\&E=(-(2+\sqrt{3})^{-1}, \sqrt{3}(2+\sqrt{3})^{-1}),~~ \beta ^-=3,~~ \beta ^+=1,~~T_h^+=\triangle DA_2E. \end{aligned} \end{aligned}$$

By a direct calculation, we find that the shape function $\phi (x)$ cannot be determined by $\phi (A_i), i=1,2,3$ in this case.

1.2 Proof of Lemma 6

Proof

First we present the following useful inequality about basis functions of the linear IFE space $S_h(T)$. Let $\phi _{A_i}\in S_h(T)$ be the basis function corresponding to a vertex $A_i$ of T defined by $\phi _{A_i}(A_j)=\delta _{ij}$. From (A.6) and (A.4), it is easy to prove that

$$\begin{aligned} |\phi _{A_i}|_{W_\infty ^m(T)}\le Ch^{-m},~ m=0,1, \end{aligned}$$

(A.10)

where the constant C is independent of h and the interface location relative to the mesh.

Derive upper bounds of$|\varUpsilon (x)|_{H^m(T)},~m=0,1$. We construct $\varUpsilon$ as follows,

$$\begin{aligned} \varUpsilon =z-I^{\mathrm{IFE}}_{h,T} z, \quad z=\left\{ \begin{aligned}&v\qquad \text{ in } T_h^+,\\&0 \qquad \text{ in } T_h^-, \end{aligned}\right. \end{aligned}$$

(A.11)

where the function v is linear and satisfies

$$\begin{aligned} \beta ^+\nabla v\cdot \mathbf{n }_h=1,\quad v(D)=v(E)=0. \end{aligned}$$

(A.12)

Here $I^{\mathrm{IFE}}_{h,T} z$ interpolates nodal values of v defined on T, i.e., $I^{\mathrm{IFE}}_{h,T} z=\sum _{i}v(A_i)\phi _{A_i}$. It is easy to verify that the constructed function $\varUpsilon$ satisfies the definitions (4.9)–(4.10). Since $v(D)=v(E)=0$, we have $\nabla v\cdot \mathbf{t }_h=0$. Thus,

$$\begin{aligned} |\nabla v|^2= |\nabla v\cdot \mathbf{n }_h|^2+ |\nabla v\cdot \mathbf{t }_h|^2\le C. \end{aligned}$$

For any point $P\in T_h^+$, using the relation $v(P)=v(D)+\nabla v\cdot \overrightarrow{DP}$, we have

$$\begin{aligned} |z|^2_{L^\infty (T)}=|v|^2_{L^\infty (T_h^+)}\le |\nabla v|^2|DP|^2\le Ch^2. \end{aligned}$$

From (A.11) and (A.10), we get the desired estimates

$$\begin{aligned} \begin{aligned}&\Vert \varUpsilon \Vert ^2_{L^2(T)}\le 2\Vert z\Vert ^2_{L^\infty (T)}|T|+2\sum _iz^2(A_i)\Vert \phi _{A_i}\Vert ^2_{L^\infty (T)}|T|\le Ch^4,\\&|\varUpsilon |^2_{H^1(T)}\le 2|\nabla v|^2|T^+_h|+2\sum _iz^2(A_i)|\phi _{A_i}|^2_{W^1_\infty (T)}|T|\le Ch^2. \end{aligned} \end{aligned}$$

Derive upper bounds of $|\varPsi _i(x)|_{H^m(T^+_h\cup T_h^-)},~i=D,E,~m=0,1$. Without loss of generality, we assume that the interface $\varGamma$ intersects with the line segments $\overline{A_1A_2}$ and $\overline{A_2A_3}$ at points D, E, respectively, see Fig. 4a for an illustration. Since the triangulation is regular, we assume that there are two constants $\alpha _{min}$ and $\alpha _{max}$ such that $\alpha _{min}\le \angle A_1A_2A_3\le \alpha _{max}$.

Let $D^\prime$ and $E^\prime$ be two points on the line DE such that $\angle DA_2E=\angle D^\prime A_1E^\prime$ and $|A_2D^\prime |=|A_2E^\prime |$, see Fig. 4c for an illustration. Then, we have the key inequality

$$\begin{aligned} |DE|\ge |D^\prime E^\prime |= 2|A_2A_{2,\perp }|\tan \frac{\angle A_1A_2A_3}{2}\ge 2|A_2A_{2,\perp }|\tan \frac{\alpha _{min}}{2}\ge C|A_2A_{2,\perp }|.\nonumber \\ \end{aligned}$$

(A.13)

Similar to (A.11), we construct $\varPsi _D(x)$ as follows,

$$\begin{aligned} \varPsi _D=z-I_{h,T}^{\mathrm{IFE}} z, \quad z=\left\{ \begin{aligned}&v\qquad \text{ in } T_h^+,\\&0 \qquad \text{ in } T_h^-, \end{aligned}\right. \end{aligned}$$

(A.14)

where the function v is linear and satisfies

$$\begin{aligned} \beta ^+\nabla v\cdot \mathbf{n }_h=0,\quad v(D)=1,\quad v(E)=0. \end{aligned}$$

(A.15)

From (A.15), we have

$$\begin{aligned} \begin{aligned} \left| \nabla v\cdot \mathbf{t }_h\right| =\frac{1}{|DE|},\quad |v(A_2)|=|v(A_{2,\perp })|=|v(E)|+|A_{2,\perp }E|\left| \nabla v\cdot \mathbf{t }_h\right| =\frac{|A_{2,\perp }E|}{|DE|}. \end{aligned} \end{aligned}$$

If $A_{2,\perp }\in \overline{T}$, then $|A_{2,\perp }E|\le |DE|$ and $|v(A_2)|=|v(A_{2,\perp })|\le 1$. Otherwise, we have $\angle A_1A_2A_3<\pi /2$. Using (A.13), we obtain

$$\begin{aligned} |v(A_2)|\le C\frac{|A_{2,\perp }E|}{|A_2A_{2,\perp }|}\le C\tan (\frac{\pi }{2}-\angle A_1A_2A_3)\le C\tan (\frac{\pi }{2}-\alpha _{min})\le C, \end{aligned}$$

Fig. 4

A diagram of an interface element

where we have used the fact that the line DE cannot be parallel to the line $A_1A_2$. Hence, we have

$$\begin{aligned} \Vert z\Vert _{L^\infty (T)}\le C~ \text{ and } ~\Vert z\Vert ^2_{L^2(T)}\le \Vert z\Vert ^2_{L^\infty (T)}|T|\le Ch^2. \end{aligned}$$

Using (A.14) and (A.10), we have

$$\begin{aligned} \Vert \varPsi _D\Vert ^2_{L^2(T)}\le C(v(A_2)\Vert \phi _{A_2}\Vert ^2_{L^\infty (T)}|T|+\Vert z\Vert ^2_{L^2(T)})\le Ch^2. \end{aligned}$$

Since v is linear, we know that

$$\begin{aligned} |z|^2_{H^1(T_h^+\cup T_h^-)}=|\nabla v|^2|T_h^+|\le \frac{|T_h^+|}{|DE|^2}\le \frac{|DE||A_2A_{2,\perp }|}{2|DE|^2}\le C, \end{aligned}$$

where we have used the equality (A.13). It follows from (A.14) and (A.10) that

$$\begin{aligned} |\varPsi _D|^2_{H^1(T_h^+\cup T_h^-)}\le C(v(A_2)|\phi _{A_2}|^2_{W^1_\infty (T)}|T| +|z|^2_{H^1(T_h^+\cup T_h^-)})\le C. \end{aligned}$$

The upper bound estimate for $\varPsi _E$ is analogous. $\square$

Appendix B: Technical results for the 3D cases

1.1 Proof of Lemma 16

Proof

$:$ Similar to (A.6) for the 2D cases, we also have

$$\begin{aligned} \phi =I_{h,T}\phi +\frac{(\beta ^-/\beta ^+-1)\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}}{1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h}(w-I_{h,T}w),\qquad \forall \phi \in S_h(T),\nonumber \\ \end{aligned}$$

(B.1)

where $T_h^+$ and $T_h^-$ in the definition of w in (A.2) are replaced by $T^+$ and $T^-$, that is,

$$\begin{aligned} w(x)=\left\{ \begin{aligned}&w^+(x)=d_{\varGamma _{h,T}^{ext}}(x)~~&\text{ in } T^+,\\&w^-(x)=0&\text{ in } T^-. \end{aligned}\right. \end{aligned}$$

(B.2)

It suffices to prove the following relation:

$$\begin{aligned} 0\le \nabla I_{h,T}w\cdot \mathbf {n}_h\le 1. \end{aligned}$$

(B.3)

There are only two types of interface elements. Type I interface element: the plane $\varGamma _{h,T}^{ext}$ cuts three edges of the tetrahedron (see Fig. 5); Type II interface element: the plane $\varGamma _{h,T}^{ext}$ cuts four edges of the tetrahedron (see Fig. 6).

Fig. 5

Type I interface element in 3D. The plane $\varGamma _{h,T}^{ext}$ cuts three edges of the element

For Type I interface element, we take the tetrahedron in Fig. 5 as an illustration. Similar to the 2D cases, we only need to consider the case $A_1\in T^+$. Let $A_{i,\perp }$ be the orthogonal projection of the point $A_i$ onto the plane $\varGamma _{h,T}^{ext}$. Similar to (A.7), we have

$$\begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h =1-\lambda _1(A_{1,\perp }), \end{aligned}$$

(B.4)

where $\lambda _i$ is the standard 3D linear basis function associated with the vertex $A_i$. Let H be the orthogonal projection of the point $A_1$ onto the plane $A_2A_3A_4$. The dihedral angle between $A_1A_2A_3$ and $A_4A_2A_3$ is denoted by $A_1\text{- }A_2A_3\text{- }A_4$. As we assume that the dihedral angles $A_1\text{- }A_2A_3\text{- }A_4, A_1\text{- }A_3A_4\text{- }A_2, A_1\text{- }A_2A_4\text{- }A_3$ are less than or equal to $\pi /2$, the point H must be on the triangle $\triangle A_2A_2A_4$ or its boundary, and there exists a point of intersection D of the line segment $\overline{A_1H}$ and the plane $\varGamma _{h,T}^{ext}$. Let $(\varGamma _{h,T}^{ext})^\perp$ be a plane that passes through the points $A_1, H$ and $A_{1,\perp }$. Obviously, we can choose a point Q, different from H, on the line of intersection of the plane $(\varGamma _{h,T}^{ext})^\perp$ and the plane $A_2A_2A_4$ such that $\varGamma _{h,T}^{ext}\cap \overline{A_1Q}\not =\emptyset$. The point of intersection of $\varGamma _{h,T}^{ext}$ and $\overline{A_1Q}$ is denoted by E.

Now we focus on the triangle $\triangle A_1HQ$ (see the right picture in Fig. 5). Let $\tilde{\lambda }_1$ be the standard 2D linear basis function on the triangle $\triangle A_1HQ$ associated with the point $A_1$. Note that $\lambda _1(H)=\lambda _1(Q)=0$ and $\lambda _1(A_1)=1$, it holds $\tilde{\lambda }_1(x)=\lambda _1(x)$ on the plane $(\varGamma _{h,T}^{ext})^\perp$. Since the maximum angle of the triangle $\triangle A_1HQ$ is equal to $\pi /2$, using the result of the 2D cases (see the proof of Lemma 1 in Appendix A.1), we obtain

$$\begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h =1-\tilde{\lambda }_1(A_{1,\perp })\in [0,1]. \end{aligned}$$

Fig. 6

Type II interface element in 3D. The plane $\varGamma _{h,T}^{ext}$ cuts four edges of the element

For Type II interface element, we take the tetrahedron in Fig. 6 as an illustration. The plane $\varGamma _{h,\varGamma }^{ext}$ intersects with the edges $\overline{A_1A_2}, \overline{A_2A_4}, \overline{A_3A_4}$ and $\overline{A_1A_3}$ at the points $D_1, D_2, D_3$ and $D_4$. In view of the limiting cases,

$$\begin{aligned} {\left\{ \begin{array}{ll} &{} {D_4\rightarrow A_1, D_3 \rightarrow A_4}~ (\text {i.e.,}\varGamma _{h,T}^{ext}\rightarrow \text {the plane }A_1A_2A_4), \\ &{} {D_2 \rightarrow A_2, D_3 \rightarrow A_3}~ (\text {i.e.,}\varGamma _{h,T}^{ext}\rightarrow \text {the plane }A_1A_2A_3),\\ &{}{D_1\rightarrow A_2, D_4\rightarrow A_3}~ (\text {i.e.,}\varGamma _{h,T}^{ext}\rightarrow \text {the plane }A_2A_3A_4),\\ &{}{D_1\rightarrow A_1, D_2 \rightarrow A_4}~ (\text {i.e.,}\varGamma _{h,T}^{ext}\rightarrow \text {the plane }A_1A_3A_4),\\ \end{array}\right. } \end{aligned}$$

the following relation must be true,

$$\begin{aligned} 0< D_4\text{- }D_1D_2\text{- }A_4< \max \{A_3\text{- }A_1A_2\text{- }A_4, A_3\text{- }A_2A_4\text{- }A_1, \pi -A_3\text{- }A_1A_4\text{- }A_2\}. \end{aligned}$$

Together with the condition $\gamma _{max}\le \pi /2$, we conclude that,

$$\begin{aligned} 0< D_4\text{- }D_1D_2\text{- }A_4<\pi -A_3\text{- }A_1A_4\text{- }A_2. \end{aligned}$$

(B.5)

Without loss of generality, we assume $A_1\in T^+$, so we have

$$\begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h =1-\lambda _1(A_{1,\perp })+(1-\lambda _4(A_{4,\perp })). \end{aligned}$$

Let $(\varGamma _{h,T}^{ext})^\perp$ be the plane that passes through the points $A_1$ and $A_4$ and is perpendicular to the plane $\varGamma _{h,T}^{ext}$. Let Q be the point of intersection of the plane $(\varGamma _{h,T}^{ext})^\perp$ and line $A_2A_3$.

Now we focus on the triangle $\triangle A_1QA_4$ (see the right picture in Fig. 6). Let $\tilde{\lambda }_1$ and $\tilde{\lambda }_4$ be the standard 2D linear basis functions on the triangle $\triangle A_1QA_4$ associated with the points $A_1$ and $A_4$, respectively. Note that $\lambda _1(A_4)=\lambda _1(Q)=0$ and $\lambda _4(A_1)=\lambda _4(Q)=0$, we have $\tilde{\lambda }_1(x)=\lambda _1(x)$ and $\tilde{\lambda }_4(x)=\lambda _4(x)$ on the plane $(\varGamma _{h,T}^{ext})^\perp$. Therefore, it holds

$$\begin{aligned} \nabla I_{h,T}w\cdot \mathbf {n}_h =1-\tilde{\lambda }_1(A_{1,\perp })+(1-\tilde{\lambda }_4(A_{4,\perp })), \end{aligned}$$

which is the same as the Eq. (A.8) for Case II in the 2D cases if we consider the triangle $\triangle A_1QA_4$. In order to use the result of the 2D cases, we need to verify the angle condition of the triangle $\triangle A_1QA_4$. In view of the relation (B.5), we consider two cases: $D_4\text{- }D_1D_2\text{- }A_4\in (0,\pi /2]$ and $D_4\text{- }D_1D_2\text{- }A_4\in [\pi /2,\pi -A_3\text{- }A_1A_4\text{- }A_2)$. If the dihedral angle $D_4\text{- }D_1D_2\text{- }A_4\in (0,\pi /2]$, then the point Q is on the ray $\overrightarrow{A_2A_3}$ and the following relation holds:

$$\begin{aligned} 0\le Q\text{- }A_1A_4\text{- }A_2<\pi /2. \end{aligned}$$

(B.6)

Note that the existence of the point Q relies on $\alpha _{max}\le \pi /2, \gamma _{max}\le \pi /2$ and the relation (B.6).

By the conditions $\angle A_2A_4A_1\le \alpha _{\max }\le \pi /2$, $Q\text{- }A_4A_2\text{- }A_1 \le \gamma _{max}\le \pi /2$, and the relation $Q\text{- }A_1A_4\text{- }A_2<\pi /2$ from (B.6), it is easy to see that $\angle QA_4A_1\le \pi /2$ (see Fig. 7 for clarity). Analogously, we have $\angle QA_1A_4\le \pi /2$ since $Q\text{- }A_1A_4\text{- }A_2<\pi /2, Q\text{- }A_1A_2\text{- }A_4\le \gamma _{\max }\le \pi /2$ and $\angle A_2A_1A_4 \le \alpha _{\max }\le \pi /2$. In view of the proof of Lemma 1 in Appendix A.1 for Case II, by the relations $\angle QA_1A_3\le \pi /2$ and $\angle QA_4A_1\le \pi /2$, we obtain the estimate (B.3). We emphasize that the condition for the angle $\angle A_1QA_4$ is actually unnecessary when the points D and E are on the edges $\overline{QA_1}$ and $\overline{QA_4}$, respectively.

If the dihedral angle $D_4\text{- }D_1D_2\text{- }A_4\in [\pi /2,\pi -A_3\text{- }A_1A_4\text{- }A_2)$, then the point Q is on the ray $\overrightarrow{A_2G}$, and it holds $0\le Q\text{- }A_1A_4\text{- }A_2<\pi /2-A_3\text{- }A_1A_4\text{- }A_2$, where the point G is on the line $A_2A_3$ but not on the ray $\overrightarrow{A_2A_3}$ (see Fig. 6). Obviously, we have $Q\text{- }A_1A_4\text{- }A_3<\pi /2$. Therefore, the proof of $\angle QA_4A_1\le \pi /2$ and $\angle QA_1A_4\le \pi /2$ is similar to that of the case $D_4\text{- }D_1D_2\text{- }A_4\in (0,\pi /2]$. $\square$

Fig. 7

Estimate the angle $\angle QA_4A_1$

1.2 Proof of Lemma 17

Proof

$:$ Let $A_i$ be a vertice of the element T, and $\phi _{A_i}$ be the corresponding IFE basis function. Similar to the 2D cases, using (B.1)–(B.3) we obtain

$$\begin{aligned} |\phi _{A_i}|_{W_\infty ^m(T^+\cup T^-)}\le Ch^{-m},~ m=0,1. \end{aligned}$$

The function $\varPsi (x)$ can be constructed explicitly as

$$\begin{aligned} \varPsi =z-I_{h,T}^\mathrm{IFE}z, \quad \quad z(x)=\left\{ \begin{aligned}&1\quad&\text{ in } T^+,\\&0&\text{ in } T^-. \end{aligned} \right. \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} |\varPsi |_{W^m_\infty (T^+\cup T^-)}&\le |z|_{W^m_\infty (T^+\cup T^-)}+\Vert z\Vert _{L^\infty (T)}\sum _{i}|\phi _{A_i}|_{W^m_\infty (T^+\cup T^-)}\le Ch^{-m}, \end{aligned} \end{aligned}$$

which implies $|\varPsi |^2_{H^m(T^+\cup T^-)}\le Ch^{3-2m}$. The estimates for $\varUpsilon$ and $\varTheta _i$ can be obtained similarly by constructing these function as

$$\begin{aligned} \varUpsilon =z-I_{h,T}^\mathrm{IFE}z,\quad \quad z(x)=\left\{ \begin{aligned}&\frac{1}{\beta ^+}(x-x^*)\cdot \mathbf {n}_h\quad&\text{ in } T^+,\\&0&\text{ in } T^-, \end{aligned} \right. \end{aligned}$$

and

$$\begin{aligned} \varTheta _{i}=z-I_{h,T}^\mathrm{IFE}z,\quad \quad z(x)=\left\{ \begin{aligned}&(x-x^*)\cdot \mathbf {t}_{i,h}\quad&\text{ in } T^+,\\&0&\text{ in } T^-. \end{aligned} \right. \end{aligned}$$

$\square$

1.3 Proof of Lemma 12 for the 3D cases

Proof

$:$ Since $I_h\phi$ is continuous across each face of the triangulation, it holds

$$\begin{aligned} \Vert [\phi ]_e\Vert ^2_{L^2(e)}=\Vert [\phi -I_h\phi ]_e\Vert ^2_{L^2(e)}\le C\sum _{i=1,2}\left\| (\phi -I_h\phi )|_{T_i}\right\| ^2_{L^2(e)}. \end{aligned}$$

(B.7)

It suffices to estimate the term on an element T with e as its face. By (B.1)–(B.3), we have

$$\begin{aligned} \left\| (\phi -I_{h}\phi )|_{T}\right\| ^2_{L^2(e)}\le Ch^2|e||\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}|^2\le Ch\Vert \nabla I_{h,T}\phi \cdot {\mathbf {n}_h}\Vert _{L^2(T)}^2. \end{aligned}$$

(B.8)

Using the identity (B.1) we also have

$$\begin{aligned} \nabla I_{h,T}\phi \cdot \mathbf {n}_h=\frac{\left( 1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h\right) (\nabla \phi ^\pm \cdot \mathbf {n}_h)}{1+(\beta ^-/\beta ^+-1)\nabla w^\pm \cdot \mathbf {n}_h}. \end{aligned}$$

By the definition of w in (B.2) and the estimate (B.3), we get

$$\begin{aligned} |\nabla I_{h,T}\phi \cdot \mathbf {n}_h|\le C|\nabla \phi ^+\cdot \mathbf {n}_h| ~~ \text{ and } ~~|\nabla I_{h,T}\phi \cdot \mathbf {n}_h|\le C|\nabla \phi ^-\cdot \mathbf {n}_h|, \end{aligned}$$

which leads to

$$\begin{aligned} \Vert \nabla I_{h,T}\phi \cdot {\mathbf {n}_h}\Vert _{L^2(T)}^2= & {} |\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}|^2|T^+|+|\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}|^2||T^-|\nonumber \\\le & {} C|\nabla \phi ^+\cdot \mathbf {n}_h|^2|T^+|+C|\nabla \phi ^-\cdot \mathbf {n}_h||T^-|\nonumber \\\le & {} C\Vert \nabla \phi \Vert ^2_{L^2(T)}. \end{aligned}$$

(B.9)

The desired result (4.48) now follows from (B.7)–(B.9). $\square$

1.4 Proof of Lemma 18

Proof

$:$ Note that $T^\triangle =(T_h^+\backslash T^+)\cup (T_h^-\backslash T^-)$ is the mis-matched region on T. For any $\phi \in S_h(T)$, it follows from (B.1)–(B.2) that for $m=0,1$,

$$\begin{aligned} \begin{aligned} |\phi ^+-\phi ^-|_{W^m_\infty (T^\triangle )}&=\left| \frac{(\beta ^-/\beta ^+-1)\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}}{1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h}\right| |d_{\varGamma _{h,T}^{ext}}|_{W^m_\infty (T^\triangle )}\le Ch^{2-2m}|\nabla I_{h,T} \phi \cdot \mathbf {n}_h|, \end{aligned} \end{aligned}$$

where in the last inequality we have utilized (B.3) and the first inequality in (6.1). The first inequality in (6.1) also implies $|T^\triangle |/|T|\le Ch$. By the definition of $\widehat{I_{h}^\mathrm{IFE}}$ in (6.15) and the inequality (B.9) we have

$$\begin{aligned} \begin{aligned} |\widehat{I_{h}^\mathrm{IFE}}\phi -\phi |^2_{H^m(T)}&=|\phi ^+-\phi ^-|^2_{H^m(T^\triangle )}\le Ch^{4-4m}|\nabla I_{h,T} \phi \cdot \mathbf {n}_h|^2|T|(|T^\triangle |/|T|)\\&\le Ch^{5-4m}\Vert \nabla I_{h,T} \phi \cdot \mathbf {n}_h\Vert ^2_{L^2(T)}\le Ch^{5-4m}\Vert \nabla \phi \Vert ^2_{L^2(T)}, \end{aligned}\nonumber \\ \end{aligned}$$

(B.10)

and

$$\begin{aligned} \begin{aligned} |\widehat{I_{h}^\mathrm{IFE}}\phi -\phi |^2_{L^2(e)}&=|\phi ^+-\phi ^-|^2_{L^2(e)}\le Ch^{4}|\nabla I_{h,T} \phi \cdot \mathbf {n}_h|^2|T|(|e|/|T|)\\&\le Ch^{3}\Vert \nabla I_{h,T} \phi \cdot \mathbf {n}_h\Vert ^2_{L^2(T)}\le Ch^{3}\Vert \nabla \phi \Vert ^2_{L^2(T)}. \end{aligned} \end{aligned}$$

(B.11)

Choosing $\phi =I_{h}^\mathrm{IFE}v$, we get

$$\begin{aligned} \widehat{I_{h}^\mathrm{IFE}}\phi -\phi =\widehat{I_{h}^\mathrm{IFE}}(I_{h}^\mathrm{IFE}v)-I_{h}^\mathrm{IFE}v=\widehat{I_{h}^\mathrm{IFE}}v-I_{h}^\mathrm{IFE}v, \end{aligned}$$

which together with (B.10) and (B.11) yields the desired results (6.16). $\square$

1.5 Proof of Lemma 19

Proof

$:$ By the Cauchy–Schwarz inequality we have

$$\begin{aligned} \left| \int _{\varGamma }\beta ^- \nabla u^-\cdot \mathbf {n} [v_h]_\varGamma ds\right| ^2\le C\Vert \nabla u^-\cdot \mathbf {n}\Vert ^2_{L^2(\varGamma )}\sum _{T\in \mathcal {T}_h^\varGamma }\Vert [v_h]_{\varGamma }\Vert ^2_{L^2(\varGamma \cap T)}. \end{aligned}$$

(B.12)

For any $\phi \in S_h(T)$, it follows from (B.1)–(B.2) that

$$\begin{aligned} \begin{aligned} \Vert [\phi ]_{\varGamma \cap T}\Vert _{L^\infty (\varGamma \cap T)}&=\left| \frac{(\beta ^-/\beta ^+-1)\nabla I_{h,T}\phi \cdot {\mathbf {n}_h}}{1+(\beta ^-/\beta ^+-1)\nabla I_{h,T}w\cdot \mathbf {n}_h}\right| \Vert d_{\varGamma _{h,T}^{ext}}\Vert _{L^\infty (\varGamma \cap T)}\le Ch^2|\nabla I_{h,T} \phi \cdot \mathbf {n}_h|, \end{aligned} \end{aligned}$$

where in the last inequality we have used (B.3) and the first inequality in (6.1). Using the fact $|\varGamma \cap T|\le Ch^2$ which can be obtain by applying the interface trace inequality (see Lemma 3.2 in [49]) to a constant function, we further have

$$\begin{aligned} \Vert [\phi ]_{\varGamma \cap T}\Vert ^2_{L^2(\varGamma \cap T)}\le Ch^6|\nabla I_{h,T} \phi \cdot \mathbf {n}_h|^2\le Ch^{3}\Vert \nabla I_{h,T} \phi \cdot \mathbf {n}_h\Vert ^2_{L^2(T)}\le Ch^{3}\Vert \phi \cdot \mathbf {n}_h\Vert ^2_{L^2(T)}, \end{aligned}$$

where we have used (B.9) in the last inequality. The lemma follows from the above inequalities and the global trace inequality on $\varOmega ^-$. $\square$