Skip to main content
SpringerLink
Log in

A Variational Reduction and the Existence of a Fully Localised Solitary Wave for the Three-Dimensional Water-Wave Problem with Weak Surface Tension

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

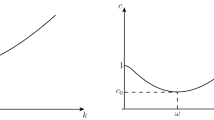
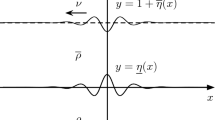
Fully localised solitary waves are travelling-wave solutions of the three- dimensional gravity–capillary water wave problem which decay to zero in every horizontal spatial direction. Their existence has been predicted on the basis of numerical simulations and model equations (in which context they are usually referred to as ‘lumps’), and a mathematically rigorous existence theory for strong surface tension (Bond number \({\beta}\) greater than \({\frac{1}{3}}\)) has recently been given. In this article we present an existence theory for the physically more realistic case \({0 < \beta < \frac{1}{3}}\). A classical variational principle for fully localised solitary waves is reduced to a locally equivalent variational principle featuring a perturbation of the functional associated with the Davey–Stewartson equation. A nontrivial critical point of the reduced functional is found by minimising it over its natural constraint set.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Similar content being viewed by others

References

  1. Ablowitz M.J., Segur H.: On the evolution of packets of water waves. J. Fluid Mech. 92, 691–715 (1979)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  2. Benci V., Cerami G.: Positive solutions of some nonlinear elliptic problems in exterior domains. Arch. Rat. Mech. Anal. 99, 283–300 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  3. Benjamin T.B., Olver P.J.: Hamiltonian structure, symmetries and conservation laws for water waves. J. Fluid Mech. 125, 137–185 (1982)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  4. Buffoni, B: Existence of fully localised water waves with weak surface tension. Mathematisches Forschungsinstitut Oberwolfach, Report no 19/2015, 1037–1039, 2015.

  5. Buffoni B., Groves M.D., Sun S.M., Wahlén E.: Existence and conditional energetic stability of three-dimensional fully localised solitary gravity–capillary water waves. J. Differ. Equ. 254, 1006–1096 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  6. Cipolatti R.: On the existence of standing waves for a Davey–Stewartson system. Commun. Part. Differ. Equ. 17, 967–988 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  7. Craig W.: Water waves, Hamiltonian systems and Cauchy integrals. In Microlocal Analysis and Nonlinear Waves (Eds. Beals M., Melrose R. B. and Rauch J.) Springer, New York, 37–45, 1991.

  8. Dias F., Kharif C.: Nonlinear gravity and capillary–gravity waves. Ann. Rev. Fluid Mech. 31, 301–346 (1999)

    Article  ADS  MathSciNet  Google Scholar 

  9. Djordjevic V.D., Redekopp L.G.: On two-dimensional packets of capillary–gravity waves. J. Fluid Mech. 79, 703–714 (1977)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Ekeland I.: On the variational principle. J. Math. Anal. Appl. 47, 324–353 (1974)

    Article  MathSciNet  MATH  Google Scholar 

  11. Groves M.D., Sun S.-M.: Fully localised solitary-wave solutions of the three-dimensional gravity–capillary water-wave problem. Arch. Rat. Mech. Anal. 188, 1–91 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  12. Hörmander L.: Lectures on Nonlinear Hyperbolic Differential Equations. Springer, Heidelberg (1997)

    MATH  Google Scholar 

  13. Kadomtsev B.B., Petviashvili V.I.: On the stability of solitary waves in weakly dispersing media. Sov. Phys. Dokl. 15, 539–541 (1970)

    ADS  MATH  Google Scholar 

  14. Lions P.L.: The concentration-compactness principle in the calculus of variations. The locally compact case, part 1. Ann. Inst. Henri Poincaré Anal. Non Linéaire 1, 109–145 (1984)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  15. Lions P.L.: The concentration-compactness principle in the calculus of variations. The locally compact case, part 2. Ann. Inst. Henri Poincaré Anal. Non Linéaire 1, 223–283 (1984)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  16. Papanicolaou G.C., Sulem C., Sulem P.L., Wang X.P.: The focusing singularity of the Davey–Stewartson equations for gravity–capillary surface waves. Physica D 72, 61–86 (1994)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  17. Parau, E.I., Vanden-Broeck, J.-M., Cooker, M.J.: Three-dimensional gravity–capillary solitary waves in water of finite depth and related problems. Phys. Fluids 17, 122101, 2005.

  18. Willem M.: Minimax Theorems. Birkhäuser, Boston (1996)

    Book  MATH  Google Scholar 

  19. Zakharov V.E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194 (1968)

    Article  ADS  Google Scholar 

  20. Zakharov V.E., Kuznetsov E.A.: Three-dimensional solitons. Zh. Eksp. Teor. Fiz. 66, 594–597 (1974)

    ADS  Google Scholar 

  21. Zakharov V.E., Kuznetsov E.A.: Hamiltonian formalism for systems of hydrodynamic type. Sov. Sci. Rev. Sec. C: Math. Phys. Rev. 4, 167–220 (1984)

    MathSciNet  MATH  Google Scholar 

  22. Zakharov V.E., Kuznetsov E.A.: Hamiltonian formalism for nonlinear waves. Physics-Uspekhi 40, 1087–1116 (1997)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Section de mathématiques, Station 8, Ecole Polytechnique Fédérale de Lausanne, 1015, Lausanne, Switzerland

    Boris Buffoni

  2. Fachrichtung Mathematik, Universität des Saarlandes, Postfach 151150, 66041, Saarbrücken, Germany

    Mark D. Groves

  3. Department of Mathematical Sciences, Loughborough University, Loughborough, LE11 3TU, UK

    Mark D. Groves

  4. Centre for Mathematical Sciences, Lund University, P.O. Box 118, 22100, Lund, Sweden

    Erik Wahlén

Authors
  1. Boris Buffoni
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mark D. Groves
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erik Wahlén
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Boris Buffoni.

Additional information

Communicated by P. Rabinowitz

M. D. Groveswould like to thank theKnut andAliceWallenberg Foundation for funding a visiting professorship at Lund University during which this paper was prepared. E.Wahlén was supported by the Swedish Research Council (Grant No. 621-2012-3753).

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Buffoni, B., Groves, M.D. & Wahlén, E. A Variational Reduction and the Existence of a Fully Localised Solitary Wave for the Three-Dimensional Water-Wave Problem with Weak Surface Tension. Arch Rational Mech Anal 228, 773–820 (2018). https://doi.org/10.1007/s00205-017-1205-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-017-1205-1

Search

Navigation