Skip to main content
SpringerLink
Log in

Solitons and Scattering for the Cubic–Quintic Nonlinear Schrödinger Equation on \({\mathbb{R}^3}\)

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

We consider the cubic–quintic nonlinear Schrödinger equation:

$$i\partial_t u = -\Delta u - |u|^2u + |u|^4u.$$

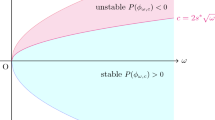
In the first part of the paper, we analyze the one-parameter family of ground state solitons associated to this equation with particular attention to the shape of the associated mass/energy curve. Additionally, we are able to characterize the kernel of the linearized operator about such solitons and to demonstrate that they occur as optimizers for a one-parameter family of inequalities of Gagliardo–Nirenberg type. Building on this work, in the latter part of the paper we prove that scattering holds for solutions belonging to the region \({{\mathcal{R}}}\) of the mass/energy plane where the virial is positive. We show that this region is partially bounded by solitons also by rescalings of solitons (which are not soliton solutions in their own right). The discovery of rescaled solitons in this context is new and highlights an unexpected limitation of any virial-based methodology.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Akahori, T., Ibrahim, S., Kikuchi, H., Nawa, H.: Existence of a ground state and blow-up problem for a nonlinear Schrödinger equation with critical growth. Differ. Integral Equ. 25(3–4), 383–402 (2012)

  2. Akahori T., Ibrahim S., Kikuchi H., Nawa H.: Existence of a ground state and scattering for a nonlinear Schrödinger equation with critical growth. Sel. Math. (N.S.) 19(2), 545–609 (2013)

    Article  MATH  Google Scholar 

  3. Akahori T., Nawa H.: Blowup and scattering problems for the nonlinear Schrödinger equations. Kyoto J. Math. 53, 629–672 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  4. Anderson D.L.T.: Stability of time-dependent particlelike solutions in nonlinear field theories. II. J. Math. Phys. 12(6), 945–952 (1971)

    Article  ADS  Google Scholar 

  5. Bahouri H., Gérard P.: High frequency approximation of solutions to critical nonlinear wave equations. Am. J. Math. 121, 131–175 (1999)

    Article  MathSciNet  MATH  Google Scholar 

  6. Begout P., Vargas A.: Mass concentration phenomena for the L 2-critical nonlinear Schrödinger equation. Trans. Am. Math. Soc. 359, 5257–5282 (2007)

    Article  MATH  Google Scholar 

  7. Berestycki H., Cazenave T.: Instabilité des états stationnaires dans les équations de Schrödinger et de Klein-Gordon non linéaires. C. R. Acad. Sci. Paris Sér. I Math. 293(9), 489–492 (1981)

    MathSciNet  MATH  Google Scholar 

  8. Berestycki H., Lions P.-L.: Nonlinear scalar field equations. I. Existence of a ground state. Arch. Ration. Mech. Anal. 82(4), 313–345 (1983)

    MathSciNet  MATH  Google Scholar 

  9. Béthuel F., Gravejat P., Saut J.-C.: Travelling waves for the Gross–Pitaevskii equation II. Commun. Math. Phys. 285, 567–651 (2009)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  10. Bourgain J.: Global well-posedness of defocusing critical nonlinear Schrödinger equation in the radial case. J. Am. Math. Soc. 12(1), 145–171 (1999)

    Article  MATH  Google Scholar 

  11. Brézis H., Lieb E.: A relation between pointwise convergence of functions and convergence of functionals. Proc. Am. Math. Soc. 88(3), 486–490 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  12. Brothers J.E., Ziemer W.P.: Minimal rearrangements of Sobolev functions. J. Reine Angew. Math. 384, 153–179 (1988)

    MathSciNet  MATH  Google Scholar 

  13. Buslaev V.B., Grikurov V.E.: Simulation of instability of bright solitons for NLS with saturating nonlinearity. IMACS J. Math. Comput. Simul. 56(6), 539–546 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  14. Carles R., Keraani S.: On the role of quadratic oscillations in nonlinear Schrödinger equation II. The L 2-critical case. Trans. Am. Math. Soc. 359, 33–62 (2007)

    Article  MATH  Google Scholar 

  15. Cazenave, T.: Semilinear Schrödinger Equations. Courant Lecture Notes in Mathematics, Vol. 10. American Mathematical Society, Providence, RI, 2003

  16. Clausius, R.: On a mechanical theorem applicable to heat. Philos. Mag. Ser. 4 40, 122–127 (1870)

  17. Coddington, E.A., Levinson, N.: Theory of Ordinary Differential Equations. McGraw-Hill Book Company, Inc., New York, 1955

  18. Coffman C.V.: Uniqueness of the ground state solution for \({\Delta u-u+u^3=0}\) and a variational characterization of other solutions. Arch. Ration. Mech. Anal. 46, 81–95 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  19. Colliander J., Keel M., Staffilani G., Takaoka H., Tao T.: Global well-posedness and scattering for the energy-critical nonlinear Schrödinger equation in \({\mathbb{R}^3}\). Ann. Math. (2) 167(3), 767–865 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  20. Desyatnikov A., Maimistov A., Malomed B.: Three-dimensional spinning solitons in dispersive media with the cubic–quintic nonlinearity. Phys. Rev. E. 61(3), 3107–3113 (2000)

    Article  ADS  Google Scholar 

  21. Dodson, B.: Global well-posedness and scattering for the defocusing, L 2-critical nonlinear Schrödinger equation when \({d\geq 3}\). J. Am. Math. Soc. 25(2), 429–463 (2012)

  22. Duyckaerts T., Holmer J., Roudenko S.: Scattering for the non-radial 3D cubic nonlinear Schrödinger equation. Math. Res. Lett. 15(6), 1233–1250 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  23. Duyckaerts T., Roudenko S.: Threshold solutions for the focusing 3D cubic Schrödinger equation. Rev. Mat. Iberoam. 26(1), 1–56 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  24. Fang D., Xie J., Cazenave T.: Scattering for the focusing energy-subcritical nonlinear Schrödinger equation. Sci. China Math. 54, 2037–2062 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Fibich G., Merle F.: Self-focusing on bounded domains. Phys. D 155(1–2), 132–158 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  26. Fröhlich J., Jonsson B.L.G., Lenzmann E.: Boson stars as solitary waves. Commun. Math. Phys. 274(1), 1–30 (2007)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  27. Gammal, A., Frederico, T., Tomio, Lauro., Abdullaev, F. Kh.: Stability analysis of the D-dimensional nonlinear Schrödinger equation with trap and two- and three-body interactions. Phys. Lett. A 267, 305–311 (2000)

  28. Gammal A., Frederico T., Tomio Lauro., Chomaz Ph.: Atomic Bose–Einstein condensation with three-body interactions and collective excitations. J. Phys. B At. Mol. Opt. Phys. 33, 4053–4067 (2000)

    Article  ADS  Google Scholar 

  29. Gérard, P., Meyer, Y., Oru, F.: Inégalités de Sobolev précisées. Séminaire É.D.P. (1996–1997), Exp. No. IV

  30. Gérard P.: The Cauchy problem for the Gross–Pitaevskii equation. Ann. Inst. H. Poincaré Anal. Non Linéaire 23(5), 765–779 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  31. Gidas, B., Ni, W.M., Nirenberg, L.: Symmetry of Positive Solutions of Nonlinear Elliptic Equations in \({\mathbb{R}^n}\). Mathematical Analysis and Applications, Part A, pp. 369–402, Adv. in Math. Suppl. Stud., Vol. 7a, Academic Press, London, 1981

  32. Ginibre J., Velo G.: Smoothing properties and retarded estimates for some dispersive evolution equations. Commun. Math. Phys. 144(1), 163–188 (1992)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  33. Ginzburg V.L.: Theories of superconductivity (a few remarks). Helv. Phys. Acta 65, 173–186 (1992)

    Google Scholar 

  34. Glassey R.T.: On the blowing up of solutions to the Cauchy problem for nonlinear Schrödinger equations. J. Math. Phys. 18, 1794–1797 (1977)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  35. Grillakis M.: On nonlinear Schrödinger equations. Commun. Partial Differ. Equ. 25(9–10), 1827–1844 (2000)

    Article  MATH  Google Scholar 

  36. Gustafson S., Nakanishi K., Tsai T. P.: Scattering theory for the Gross–Pitaevskii equation in three dimensions. Commun. Contemp. Math. 11(4), 657–707 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  37. Gustafson S., Nakanishi K., Tsai T.P.: Scattering for the Gross–Pitaevskii equation. Math. Res. Lett. 13(2), 273–285 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  38. Ionescu A.D., Pausader B.: The energy-critical defocusing NLS on \({\mathbb{T}^3}\). Duke Math. J. 161(8), 1581–1612 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  39. Keel M., Tao T.: Endpoint Strichartz estimates. Am. J. Math. 120(5), 955–980 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  40. Kenig C., Merle F.: Global well-posedness, scattering and blow-up for the energy-critical, focusing, non-linear Schrödinger equation in the radial case. Invent. Math. 166(3), 645–675 (2006)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  41. Keraani S.: On the defect of compactness for the Strichartz estimates for the Schrödinger equations. J. Differ. Equ. 175(2), 353–392 (2001)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  42. Keraani S.: On the blow-up phenomenon of the critical nonlinear Schrödinger equation. J. Funct. Anal. 235, 171–192 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  43. Killip R., Kwon S., Shao S., Vişan M.: On the mass-critical generalized KdV equation. Discrete Contin. Dyn. Syst. 32(1), 191–221 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  44. Killip R., Oh T., Pocovnicu O., Vişan M.: Global well-posedness of the Gross–Pitaevskii and cubic–quintic nonlinear Schrödinger equations with non-vanishing boundary conditions. Math. Res. Lett. 19(5), 969–986 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  45. Killip R., Stovall B., Visan M.: Scattering for the cubic Klein–Gordon equation in two space dimensions. Trans. Am. Math. Soc. 364(3), 1571–1631 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  46. Killip R., Vişan M.: The focusing energy-critical nonlinear Schrödinger equation in dimensions five and higher. Am. J. Math. 132(2), 361–424 (2010)

    Article  MATH  Google Scholar 

  47. Killip R., Vişan M.: Global well-posedness and scattering for the defocusing quintic NLS in three dimensions. Anal. PDE 5(4), 855–885 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  48. Killip, R., Vişan, M.: Nonlinear Schrödinger Equations at Critical Regularity. Evolution equations, 325–437, Clay Math. Proc., Vol. 17. Amer. Math. Soc., Providence, RI, 2013

  49. Killip R., Vişan M., Zhang X.: Quintic NLS in the exterior of a strictly convex obstacle. Am. J. Math. 138(5), 1193–1346 (2016)

    Article  MathSciNet  Google Scholar 

  50. Koch, H., Tataru, D., Vişan, M.: Dispersive Equations and Nonlinear Waves. Generalized Korteweg–de Vries, Nonlinear Schrödinger, Wave and Schrödinger Maps. Oberwolfach Seminars, Vol. 45. Birkhäuser, Basel, 2014

  51. Kolodner I.I.: Heavy rotating string—a nonlinear eigenvalue problem. Commun. Pure Appl. Math. 8, 395–408 (1955)

    Article  MathSciNet  MATH  Google Scholar 

  52. Kwong, M.K.: Uniqueness of positive solutions of \({\Delta u-u+u^p=0}\) in \({\mathbb{R}^n}\). Arch. Ration. Mech. Anal. 105(3), 243–266 (1989)

  53. Le Coz, S., Martel, Y., Raphaël, P.: Minimal mass blow up solutions for a double power nonlinear Schrödinger equation. Rev. Mat. Iberoam. 32(3), 795–833 (2016)

  54. LeMesurier B.J., Papanicolaou G., Sulem C., Sulem P.-L.: Focusing and multi-focusing solutions of the nonlinear Schrödinger equation. Phys. D 31(1), 78–102 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  55. Lions P.-L.: The concentration-compactness principle in the calculus of variations. The locally compact case. I. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(2), 109–145 (1984)

    Article  ADS  MATH  Google Scholar 

  56. Mariş, M.: Travelling waves for nonlinear Schrödinger equations with nonzero conditions at infinity. Ann. Math. (2) 178(1), 107–182 (2013)

  57. McLeod, K.: Uniqueness of positive radial solutions of \({\Delta u+f(u)}\) in \({\mathbb{R}^n}\). II. Trans. Am. Math. Soc. 339(2), 495–505 (1993)

  58. Merle F., Raphaël P.: Blow up of the critical norm for some radial L 2 super critical nonlinear Schrödinger equations. Am. J. Math. 130(4), 945–978 (2008)

    Article  MATH  Google Scholar 

  59. Merle F., Vega L.: Compactness at blow-up time for L 2 solutions of the critical nonlinear Schrödinger equation in 2D. Int. Math. Res. Not. 8, 399–425 (1998)

    Article  MATH  Google Scholar 

  60. Miao C., Xu G., Zhao L.: The dynamics of the 3D radial NLS with the combined terms. Commun. Math. Phys. 318(3), 767–808 (2013)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  61. Mihalache D., Mazilu D., Crasovan L.-C., Malomed B.A., Lederer F.: Three-dimensional spinning solitons in the cubic–quintic nonlinear medium. Phys. Rev. E 61(6), 7142–7145 (2000)

    Article  ADS  Google Scholar 

  62. Mihalache D., Mazilu D., Crasovan L.-C., Towers I., Buryak A.V., Malomed B.A., Torner L.: Stable spinning solitons in three dimensions. Phys. Rev. Lett. 88(7), 4 (2002)

    Article  Google Scholar 

  63. Nakanishi, K., Schlag, W.: Invariant Manifolds and Dispersive Hamiltonian Evolution Equations. Zurich Lectures in Advanced Mathematics. European Mathematical Society (EMS), Zürich, 2011

  64. Nakanishi K., Schlag W.: Global dynamics above the ground state energy for the cubic NLS equation in 3D. Calc. Var. Partial Differ. Equ. 44(1–2), 1–45 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  65. Payne L.E., Sattinger D.H.: Saddle points and instability of nonlinear hyperbolic equations. Isr. J. Math. 22(3–4), 273–303 (1975)

    Article  MathSciNet  MATH  Google Scholar 

  66. Reed, M., Simon, B.: Methods of Modern Mathematical Physics. IV. Analysis of Operators. Academic Press, London, 1978

  67. Serrin J., Tang M.: Uniqueness of ground states for quasilinear elliptic equations. Indiana Univ. Math. J. 49(3), 897–923 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  68. Shatah J., Strauss W.: Instability of nonlinear bound states. Commun. Math. Phys. 100(2), 173–190 (1985)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  69. Strichartz R.S.: Restrictions of Fourier transforms to quadratic surfaces and decay of solutions of wave equations. Duke Math. J. 44(3), 705–714 (1977)

    Article  MathSciNet  MATH  Google Scholar 

  70. Sulem, C., Sulem, P.-L.: The Nonlinear Schrödinger Equation. Self-Focusing and Wave Collapse. Applied Mathematical Sciences, Vol. 139. Springer, New York, 1999

  71. Tao T., Vişan M., Zhang X.: The nonlinear Schrödinger equation with combined power-type nonlinearities. Commun. Partial Differ. Equ. 32(7–9), 1281–1343 (2007)

    Article  MATH  Google Scholar 

  72. Vlasov S.N., Petrishchev V.A., Talanov V.I.: Averaged description of wave beams in linear and nonlinear media (the method of moments). Radiophys. Quantum Electron. 14, 1062–1070 (1971)

    Article  ADS  Google Scholar 

  73. Weinstein, M.: Nonlinear Schrödinger equations and sharp interpolation estimates. Comm. Math. Phys. 87(4), 567–576 (1982/83)

  74. Weinstein M.: Modulational stability of ground states of nonlinear Schrödinger equations. SIAM J. Math. Anal. 16(3), 472–491 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  75. Yajima K.: Existence of solutions for Schrödinger evolution equations. Commun. Math. Phys. 110(3), 415–426 (1987)

    Article  ADS  MathSciNet  MATH  Google Scholar 

  76. Zhang X.: On the Cauchy problem of 3-D energy-critical Schrödinger equations with subcritical perturbations. J. Differ. Equ. 230(2), 422–445 (2006)

    Article  ADS  MATH  Google Scholar 

  77. Zhou C., He X.T.: Stochastic diffusion of electrons in evolutive Langmuir fields. Phys. Scr. 50, 415–418 (1994)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of California, Los Angeles, Los Angeles, CA, 90095, USA

    Rowan Killip

  2. School of Mathematics, The University of Edinburgh, James Clerk Maxwell Building, The King’s Buildings, Mayfield Road, Edinburgh, EH9 3JZ, UK

    Tadahiro Oh

  3. The Maxwell Institute for the Mathematical Sciences, James Clerk Maxwell Building, The King’s Buildings, Mayfield Road, Edinburgh, EH9 3JZ, UK

    Tadahiro Oh

  4. Department of Mathematics, Princeton University, Fine Hall, Washington Rd., Princeton, NJ, 08544-1000, USA

    Oana Pocovnicu

  5. School of Mathematics, Institute for Advanced Study, Einstein Dr., Princeton, NJ, 08540, USA

    Oana Pocovnicu

  6. Department of Mathematics, Heriot-Watt University, Edinburgh, EH14 4AS, UK

    Oana Pocovnicu

  7. The Maxwell Institute for the Mathematical Sciences, Edinburgh, EH14 4AS, UK

    Oana Pocovnicu

  8. Department of Mathematics, University of California, Los Angeles, Los Angeles, CA, 90095, USA

    Monica Vişan

Authors
  1. Rowan Killip
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tadahiro Oh
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Oana Pocovnicu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Monica Vişan
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rowan Killip.

Additional information

Communicated by S. Serfaty

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Killip, R., Oh, T., Pocovnicu, O. et al. Solitons and Scattering for the Cubic–Quintic Nonlinear Schrödinger Equation on \({\mathbb{R}^3}\) . Arch Rational Mech Anal 225, 469–548 (2017). https://doi.org/10.1007/s00205-017-1109-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-017-1109-0

Search

Navigation