1 Introduction

Silicone rubber materials are long-established in the electronics industry. Silica-reinforced silicones, for instance, are widely used for both the assembly and the encapsulation of electronic devices, thanks to their interesting properties in terms of sealing and thermal stability [1]. Also, the last decades have seen the rise of electrically conductive silicone rubbers that, thanks to the addition of metallic fillers in high proportion (such as silver, copper and aluminum), are able to conduct electric signals. Electrically conductive adhesives are proved to have good mechanical strength and excellent electrical conductivity [2, 3]. Therefore, they are adequate replacements for conventional assembly techniques in the electronics industry, as they are simpler and safer to implement than procedures like brazing and soldering [4, 5].

These composite materials withstand extreme working conditions during their lifetime, like high temperatures [6], moisture [7] and chemicals that degrade the integrity of the assembly, such as oxygen, hydrogen and others [8]. These conditions trigger aging reactions that permanently modify the properties of the materials, leading to the deterioration of their properties and lifetime reduction. Moreover, these materials are subjected to various mechanical loads, coming from impact and vibrations [9], as well as differential expansion due to coefficient of thermal expansion (CTE) mismatch [10]. The study of their mechanical behavior and aging mechanisms is therefore crucial to their reliability assessment.

The impact of chemical aging to the mechanical behavior of rubber-like materials has been thoroughly treated in literature. Johlitz [11] mentions that, globally, two types of mechanisms can trigger changes of a polymer during chemical aging: chain scissions and cross-linking reformation. The first mechanism refers to the degradation of molecular bonds on the polymer chains and usually leads to a softening of the elastomer, while the latter refers to an aging-induced formation of new cross-linking points, generally leading to a stiffer and less flexible material [12]. Examples of possible cause of chemical aging in elastomers are high temperatures [13], oxidation [14, 15] and exposure to radiation [16].

For the case of silicone rubbers, many aging conditions have been investigated. For instance, Camino et al. [17, 18] quantify and explain the thermal degradation of PDMS in an inert atmosphere. Under high temperatures, the polymer goes through a chain scission process in the Si-O links of its main backbones, leading to the outgassing of oligomer decomposition products (mainly hexamethylcyclotrisiloxane). They also proved that the aging kinetics is modified under the presence of oxygen in the atmosphere. Tomer et al. [19] studied the oxidation, chain scission and cross-linking formation of silicone rubbers upon different types of aging and proposed chemical pathways that explain the aging-related changes in the material behavior. Wang et al. [20] studied the thermo-oxidative aging of silicone rubber under temperatures up to 250 \(^{\circ }\)C and found that, in those conditions, cross-linking reactions drive the changes in the material, whose hardness increases with aging time and temperature. Kashi et al. [21] observed a decrease in both the tensile strength and the elongation at break for silicone rubber after accelerated aging in oil. Regarding the aging conditions specific to high-performance electronics, some previous works exist [22, 23], but many subjects are yet to be addressed, specially in the context of aging in hermetic environments.

This work proposes both the measurement and the modeling of the mechanical properties of filled silicone rubber after aging in a hermetic environment at extreme temperatures. Measurement of viscoelastic properties is done through torsional Dynamic Mechanical Analysis (DMA). These tests allow to characterize the materials in their unaged state and to observe the changes in the material behavior induced by aging. Following the experimental study, an aging-dependent generalized Maxwell model is proposed with the objective of modeling the viscoelastic behavior of the materials as a function of aging time and temperature.

2 Materials and methods

This section presents the silicone materials that are analyzed in this study, the procedure of the sample manufacturing, the aging conditions they are subjected to and the principle of the mechanical tests performed.

2.1 Materials and specimen preparation

Three commercially available silicone-based adhesive materials used for the assembly of electronic devices are investigated. These composite materials are composed of a polymer matrix that is reinforced with fillers. The composition of the matrix and the nature and quantity of the fillers are different for each specific product. The compositions of the three materials are listed in Table 1. These data are extracted from the Safety Data Sheets provided by the manufacturers. Therefore, the complete list of ingredients and/or their exact proportion in the mixture may not be fully disclosed in some cases due to industrial secret. All three materials are ready-to-use formulations, meaning that all the ingredients composing the final product are previously mixed by the manufacturer. The silica-filled silicones are manufactured by Dow, and the silver-filled silicones are manufactured by Henkel.

Table 1 Formulation of silicone materials expressed in mass percentage (% w/w)
Full size table

Two silica-filled materials with different filler proportion (14 % and 24 %) are studied. They are classical applications of room temperature vulcanized (RTV) silicone elastomers and their matrices are composed of polydimethylsiloxane (PDMS). They polymerize through a condensation reaction thanks to the action of the curing agent methyltrimetoxysilane, which initiates the cross-linking process in the presence of ambient humidity. Both materials have a similar chemical composition of their matrices, the essential difference between them being the quantity of reinforcing fillers.

The silver-filled material is an electrically conductive adhesive of PDMS-PMHS (bloc polymer of polydimethylsiloxane and polymethylhydrosiloxane), highly filled with silver particles for conductivity purposes. The amount of filler must be above the percolation threshold of the material. This threshold indicates the critical volume fraction of fillers needed for the material to be conductive, under the hypothesis that the metallic fillers are homogeneously spread in the matrix [24, 25]. The manufacturer provides only a range for the mass proportion of the silver-filled silicone. The precise amount of fillers was measured through density measurements and can be estimated to 84 %. In this case, the cross-linking of the network is achieved through the action of ethyl silicate 32, a thermally activated cross-linker.

Rectangular solid samples of the silicones are obtained through molding. The base material is poured into molds, and then, a 15-minute vacuum cycle is performed to decrease the initiation of voids in the cured silicone. For the case of RTV silica-filled silicones, the samples are left to polymerize in ambient temperature during 48 hours. This time is needed for the cross-linking of the network to complete. The dimensions of the samples for these materials are 30 mm \(\times \) 6 mm \(\times \) 2.8 mm (length \(\times \) width \(\times \) thickness). The silver-filled material is cured in an oven, following a precise curing cycle that is kept confidential. The dimensions of the samples for this material are 30 mm \(\times \) 10 mm \(\times \) 2 mm (length \(\times \) width \(\times \) thickness).

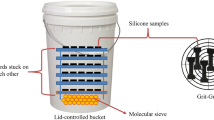
Concerning the aging conditions, the samples are aged in a hermetic environment initially filled with nitrogen. Aging is done at three temperatures (150 \(^{\circ }\)C, 180 \(^{\circ }\)C and 210 \(^{\circ }\)C) for four different times (1, 2, 3 and 6 months). The hermetic aging atmosphere is initially inert, but, as aging evolves, many compounds are bound to be outgassed and thus modify the atmosphere in which the material ages [17, 26]. This could lead to modifications in the aging reactions and their kinetics.

Given the conditions of the studied aging, the only driving force that triggers the aging reactions is temperature. Since the aging times are in the scale of months, and that the thermal homogeneity of the samples can be reached within hours, it is safe to assume that the temperature will be homogeneous through the thickness of the samples during aging. Therefore, the aging can be considered homogeneous. Besides, only chemical aging is considered in this work, as opposed to physical aging. Indeed, physical aging is relevant for polymers in a glassy state, and the studied silicones are aged and tested in their rubbery state, at temperatures considerably larger than the glass transition temperature.

2.2 Methods

The viscoelastic behavior of the filled silicone rubbers is studied through Dynamic Mechanical Analysis (DMA) in torsional mode. An Anton Paar MCR 502 rheometer is used for the experiments. This system is equipped with grips that allow the correct fixing of a rectangular specimen for the torsion test. A photograph of the setup with a mounted specimen is presented in Fig. 1.

Fig. 1
figure 1

Experimental setup: Specimen mounted in Anton Paar MCR 502 rheometer

Full size image

Two types of tests are run: amplitude sweeps for amplitudes between 0.001 % and 10 % at ambient temperature and constant frequency of 1 Hz, only for samples in their unaged state, and frequency sweeps from 0.01 to 10 Hz at ambient temperature, for both unaged and aged samples.

2.2.1 Amplitude sweep tests

Amplitude sweep tests are carried for the three silicone materials only in their unaged state, at a constant temperature of 25 \(^{\circ }\)C and a frequency of 1 Hz, for strain amplitudes ranging from \(0.001\,\%\) to \(10\,\%\). Five data points per decade are considered, which are spread evenly following a logarithmic rule. A positive tensile force is applied to avoid buckling of the specimen. The positive tensile force chosen is 0.5 N for both silica-filled silicones and 2 N for the silver-filled one. The difference in these values is explained since the silver-filled material is stiffer that the silica-filled ones, and thus, a higher value of positive tensile force should be applied to avoid buckling.

2.2.2 Frequency sweep tests

Frequency sweeps for different aging states of the studied filled silicones are performed in order to quantify the impact of aging on their viscoelastic behavior. The tests are performed at a constant temperature of 25 \(^{\circ }\)C, for frequencies between \(10^{-2}\) and 10 Hz, and applying the strain amplitudes defined through the amplitude sweeps, presented in Sect. 3.1.

3 Linear viscoelasticity characterization

This section presents the experimental results belonging to the viscoelastic properties of the three studied silicone rubbers, in their unaged and aged states.

These tests consist of applying a sinusoidal shear strain \(\gamma (t)\) and recording the shear stress \(\sigma (t)\) developed in the sample. The evolution of the imposed shear strain can be represented as

$$\begin{aligned} \gamma (t) = \gamma _0 \, \sin (\omega t) \end{aligned}$$
(1)

where \(\gamma _0\) is the strain amplitude, \(\omega \) is the angular frequency and t is time. For small strains, and in the case of a linear response of the material, the measured stress can be represented as

$$\begin{aligned} \sigma (t) = \sigma _0 \, \sin (\omega t + \delta ). \end{aligned}$$
(2)

where \(\sigma _0\) refers to the stress amplitude and the angle \(\delta \) corresponds to the phase difference between the stress and strain signals. Indeed, while for a purely elastic material the strain and stress are in phase, in the case of a viscoelastic material there will be a delay of the stress with respect to the strain signal.

Based on these quantities, it is possible to define the storage modulus (\(G^{\prime }\)), the loss modulus (\(G^{\prime \prime }\)) and the dynamic complex modulus (\(G^{*}\)) as

$$\begin{aligned} G^{\prime } = \dfrac{\sigma _0}{\gamma _0} \, \sin (\delta ) \end{aligned}$$
(3)
$$\begin{aligned} G^{\prime \prime } = \dfrac{\sigma _0}{\gamma _0} \, \cos (\delta ). \end{aligned}$$
(4)
$$\begin{aligned} G^{*} = G^{\prime } + i\,G^{\prime \prime } \end{aligned}$$
(5)

The storage modulus represents the reversible part of the dynamic mechanical material behavior, while the loss modulus accounts for the dissipative part. Their quotient allows to define the loss factor (\(\tan (\delta )\)), which measures the fraction of the energy that is dissipated in each loading cycle.

$$\begin{aligned} \tan (\delta ) = \dfrac{G^{\prime \prime }}{G^{\prime }} \end{aligned}$$
(6)

Different tests performed using this technique are presented in the following subsections.

3.1 Amplitude sweep tests

Amplitude sweep tests allow to determine the linear viscoelastic region of the material, in which its complex modulus remains almost constant. The limit strain amplitude can be determined when the storage modulus deviates from the small strain plateau with a tolerance of 10 % [27]. One of the objectives of this test is the definition of an optimal strain amplitude for the temperature and frequency sweep tests. The optimal amplitude must be low enough to ensure that the test is done in the linear regime under the small strain hypothesis [28]. However, the choice of an excessively low value can lead to noisy results due to the low torsional momentum achieved in this range.

The experimental results belonging to the amplitude sweep tests of 14 % and 24 % silica-filled silicones are shown in Figs. 2 and 3, respectively. All amplitude sweep tests were performed at least twice. For both cases, some data points acquired at very low strain amplitude values, close to 0.001 %, were disregarded due to excessive noise in the measurements. In the graphs, it is possible to see for both materials under cyclic loading at small strains, that the storage and loss modulus are independent of the applied strain amplitude. The values of the storage modulus in the small strain plateau are 0.5 MPa for the 14% silica-filled silicone, and 1.2 MPa for the 24% silica-filled one. The difference in the moduli values can be explained by the different filler proportion, the stiffer material being the on with the most reinforcing particles. For strains above 1 %, a non-linearity effect is triggered and the moduli become strain dependent. Above this limit (\(\gamma _{0_{\mathrm {lim}}}\)), the storage and loss modulus show a decrease, and the loss factor increases until it reaches a peak. Considering these results, the value \(\gamma _0 = 1\,\%\) is chosen for the temperature and frequency sweep tests of silica-filled silicones, as this value allows for an accurate measurement of the signals and a negligible effect of the non-linearity. This value also respects the drop of the storage modulus lower than 10 % proposed in the literature.

The experimental results of the silver-filled silicone are plotted in Fig. 4. The evolution of the moduli shows a plateau-like behavior for values of \(\gamma _0\) between 0.001 % and 0.01 %. The storage modulus at small strains is 166 MPa for this material, a much higher value than for the silica-filled silicones as a result of the elevated filler content. In this case, the silicone exhibits a nonlinear behavior for amplitudes larger than 0.01 %. Above this point, the material shows the signs of the Payne effect, a strain-related non-linearity that is characteristic for highly-filled materials [29]. A sharp decrease in the storage modulus is observed, while the loss modulus shows a gradual increase. The loss factor increases as well, until it reaches its peak value at an amplitude of 0.5 %. In this case, the strain amplitude \(\gamma _0 = 0.01\,\%\) is chosen for the following tests, for the same reasons explained above for the other materials.

It is interesting to point out that the filler content does not only have an impact to the stiffness of the materials, but also to the strain needed for the nonlinear behavior to manifest and the relative stiffness decrease for amplitudes above \(\gamma _{0_{\mathrm {lim}}}\). Figure 5 shows a comparison of the normalized amplitude of the complex modulus for the three materials. For the construction of these curves, the values of \(|G^{*} |\) are normalized with respect to the value of the storage modulus in the small strain plateau for each material. It is possible to see that for an applied strain of 10 %, the absolute value of the complex modulus decreases 10 % with respect to the small strain value for the 14 % silica-filled silicone, while the decrease reaches 15 % for that filled with 24 %, at the same level of strain amplitude. The effect of fillers is even more evident in the silver-filled material, which has a modulus decrease of 85 % at a strain amplitude of 4 %.

These results are taken into account for the tests presented in the following section, for which the applied strain is below the limit values. More precisely, an amplitude of \(\gamma _0=1\,\%\) is chosen for both silica-filled silicones, while \(\gamma _0=0.01\,\%\) is chosen for the silver-filled material.

Fig. 2
figure 2

Storage and loss modulus a and loss factor b as a function of strain amplitude at \(f=1\) Hz and \(\theta =25\) \(^{\circ }\)C, for 14 % silica-filled silicone

Full size image
Fig. 3
figure 3

Storage and loss modulus a and loss factor b as a function of strain amplitude at \(f=1\) Hz and \(\theta =25\) \(^{\circ }\)C, for 24 % silica-filled silicone

Full size image
Fig. 4
figure 4

Storage and loss modulus a and loss factor b as a function of strain amplitude at \(f=1\) Hz and \(\theta =25\) \(^{\circ }\)C, for silver-filled silicone

Full size image
Fig. 5
figure 5

Normalized amplitude of complex modulus as a function of the strain amplitude at \(f=1\) Hz and \(\theta =25\) \(^{\circ }\)C, for the three materials analyzed

Full size image

3.2 Frequency sweep at ambient temperatures for different aging conditions

The results for frequency sweep tests at ambient temperature for different aging conditions, namely the resulting storage and loss moduli, are plotted in Figs. 6, 7 and 8 for the three materials. Most frequency sweep tests were performed twice, with the exception of some aging conditions for which fragilization and failure during mounting occurred, and only one test could be done.

Fig. 6
figure 6

Storage and loss modulus for frequencies between \(10^{-2}\) to 10 Hz for \(\gamma _0=1\,\%\) at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of 14% silica-filled silicone

Full size image
Fig. 7
figure 7

Storage and loss modulus for frequencies between \(10^{-2}\) to 10 Hz for \(\gamma _0=1\,\%\) at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of 24% silica-filled silicone

Full size image
Fig. 8
figure 8

Storage and loss modulus for frequencies between \(10^{-2}\) to 10 Hz for \(\gamma _0=0.01\,\%\) at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of silver-filled silicone

Full size image

The effects of the aging parameters, i.e., aging time \(t_a\) and aging temperature \(\theta _a\), are clear in the results. A progressive softening of the materials is observed with respect to the unaged state, which intensifies as the aging parameters increase. This softening effect can be captured with the gradual decrease in the storage and the loss modulus. This allows to conclude that chain scissions drive the aging evolution, with regard to the mechanical properties of the material. The softening effect appears to be more pronounced for the silica-filled silicones than for the silver-filled one. This difference could be linked to the difference in the formulation and the cross-linking mechanisms.

4 Material modeling

This section presents the aging-dependent generalized Maxwell model used to describe the results shown in Sect. 3.2. It is a viscoelastic model based on a continuous spectrum of relaxation times \(H(\tau )\) and viscosities \(\eta _i\) depending on the aging parameters (\(t_a\) and \(\theta _a\)).

Fig. 9
figure 9

Schematic representation of aging-dependent generalized Maxwell model

Full size image

Figure 9 shows a representation of a generalized Maxwell model with n elements. The quantities \(G_i\) and \(\eta _i\) of each element are related to the relaxation time \(\tau _i\), such that

$$\begin{aligned} \tau _i = \dfrac{\eta _i}{G_i}. \end{aligned}$$
(7)

Similar approaches have been implemented in literature to model nonlinear viscoelastic behavior of polymers depending on different variables, such as static prestrain [30], dynamic strain for the consideration of the Payne effect [31] and physical aging [32]. The cited articles can be consulted for further information on the model construction, as they are major references of the current work.

The continuous spectrum of relaxation times can be seen as a statistical time distribution of the molecular mobility of the polymer and can be directly related to its global viscosity [33]. Taking a time-based approach in viscoelasticity, \(H(\tau )\) can be related to the relaxation modulus G(t) through the following expression

$$\begin{aligned} G(t) = G_{\infty } + \int _{-{\infty }}^{+\infty } H(\tau ) \, e^{-\frac{t}{\tau }} \, d\ln (\tau ). \end{aligned}$$
(8)

In the frequency domain, a similar relation exists between the complex dynamic modulus and the continuous spectrum of relaxation times, as follows

$$\begin{aligned} G^{*}(\omega ) = G_{\infty } + \int _{-{\infty }}^{+\infty } H(\tau ) \dfrac{i \omega \tau }{1 + i \omega \tau } \, d\ln (\tau ). \end{aligned}$$
(9)

As explained by Jalocha [32], the identification of the spectrum \(H(\tau )\) cannot be done directly from the mechanical tests. Smith [34] proposes a method to identify it from the complex modulus, but its implementation presents some difficulties. Baumgaertel et al. [35] propose to use the relaxation modulus to identity the continuous relaxation spectrum. This approach will be followed in this work. Indeed, the method by Smith employs complex quantities in the calculation of \(H(\tau )\), which can lead to singularities, is more difficult to perform and is less straight-forward than the simple equations proposed by Baumgaertel. Motivated by experience, the following analytical expression is used to fit the relaxation modulus.

$$\begin{aligned} G(t) = G_{\infty } + \dfrac{G_g}{\left( 1+\dfrac{t}{t_0}\right) ^{\beta }} , \end{aligned}$$
(10)

where \(G_{\infty }\), \(G_g\), and \(t_0\) are parameters dependent only on the material, and \(\beta \) is a parameter dependent on both the material and the state of aging. Since the identification is based on the relaxation modulus, the experimental frequency-dependent data obtained through Dynamic Mechanical Analysis must be converted to the time domain. Such conversion between the time and frequency domains is possible through analytical Fourier transform. However, simple approximate expressions exist in literature to estimate the temporal quantities from the frequency data and vice-versa [36, 37]. In this study, the approximation of Schwarzl [36] is used, as follows

$$\begin{aligned} G(t)\Bigr |_{t=\frac{1}{\omega }} \approx G^{\prime }(\omega )-0.566\,G^{\prime \prime }(\omega /2)+0.203\,G^{\prime \prime }(\omega ). \end{aligned}$$
(11)

This equation needs the values of \(G^{\prime \prime }(\omega /2)\) as an input. In this case, it has been chosen to estimate these values through interpolation of the experimental data. For the specific case of the first data point (corresponding to the minimum frequency tested), where interpolation is not possible for the value \(G^{\prime \prime }(\omega _{min}/2)\), it is obtained through extrapolation of the values of \(G^{\prime \prime }\) of the two smallest frequencies tested.

The analytical expression of \(H(\tau )\) can be found by replacing Eq. 10 in Eq. 8 and performing the Laplace transform of Eq. 8, leading to the expression

$$\begin{aligned} H\left( \tau ,\beta \right) = \dfrac{G_g}{\Gamma \left( \beta \right) } \left( \dfrac{\tau }{t_0}\right) ^{-\beta } e^{-\frac{t_0}{\tau }}. \end{aligned}$$
(12)

Therefore, the form of \(H(\tau )\) is given by the parameters \(G_g\), \(\beta \) and \(t_0\), which are found by fitting Eq. 10 to the experimental relaxation modulus.

The objective of this model is to find a direct link between the relaxation spectra and the elements in the Maxwell model. A first mathematical step toward that link is the equality between Eq. 8 and the expression for the relaxation modulus calculated from the elements of the Maxwell model, as follows

$$\begin{aligned} G_\infty + \sum _{i=1}^{n}G_i \, e^{-\frac{t}{\tau _i}} =G_\infty + \int _{-\infty }^{\infty }H(\tau ) \, e^{-\frac{t}{\tau }} \, d\ln (\tau ). \end{aligned}$$
(13)

The model requires a discretization of the space of relaxation times, which is performed by choosing a set of n relaxation times evenly distributed in a logarithmic scale. The logarithmic step between each relaxation time, named a such that \(\tau _{i+1} = \tau _i \cdot a\), can be calculated from the maximum and minimum relaxation times as

$$\begin{aligned} a = \root n \of {\frac{\tau _{max}}{\tau _{min}}}. \end{aligned}$$
(14)

A schematization of the discretized relaxation times is shown in Fig. 10.

Fig. 10
figure 10

Schematic representation of the discretization of relaxation times

Full size image

In the figure, \(\tau _i^{+}=\sqrt{\tau _{i} \cdot \tau _{i+1}}\) and \(\tau _i^{-} = \sqrt{ \tau _{i} \cdot \tau _{i-1}}\) represent the logarithmic means between \(\tau _i\) and its neighbors. For any relaxation time such that \(\tau _i^{-}< \tau < \tau _i^{+}\), it is possible to write Eq. 13 as

$$\begin{aligned} G_i \, e^{-\frac{t}{\tau _i}} =G_\infty + \int _{\tau _{i}^{-}}^{\tau _{i}^{+}}H(\tau ,\beta ) \, e^{-\frac{t}{\tau }} \, d\ln (\tau ). \end{aligned}$$
(15)

Under the hypothesis that the interval between \(\tau _{i-1}\) and \(\tau _{i+1}\) is small enough, it is possible to consider that integrand stays constant within that range and thus

$$\begin{aligned} G_i \,e^{-\frac{t}{\tau _i}} = H(\tau _i,\beta )\,e^{-\frac{t}{\tau _i}}\,\ln \left( \dfrac{\tau _{i}^{-}}{\tau _{i}^{+}}\right) . \end{aligned}$$
(16)

Considering this expression and Eq. 7, it is possible to find the following relationship between the viscosities of the generalized Maxwell model and the discretized relaxation spectrum:

$$\begin{aligned} \eta _i(\beta ) = \tau _i \,H(\tau _i,\beta )\ln \left( \sqrt{\dfrac{\tau _{i-1}}{\tau _{i+1}}}\right) . \end{aligned}$$
(17)

It is thus possible to affirm that once the relaxation times are known and discretized, the knowledge of the discretized relaxation spectrum is sufficient for the calculation of viscosities and proposal of a generalized Maxwell model. Since the relaxation spectrum depends on the aging state, which is represented by the parameter \(\beta \), the generalized Maxwell model will also be directly dependent on the aging state. The identification of the parameters \(G_\infty \), \(G_g\) and \(t_0\) as well as the evolution of \(\beta \) is therefore sufficient for the proposal of an aging-dependent model. This identification process was performed for all tested materials and is presented in Sect. 4.1. The relationship between the parameter \(\beta \) and the aging parameters will be discussed later in the article.

4.1 Application to experimental data

The presented model is applied to the experimental data provided in Sect. 3.2. For simplification, the entire identification procedure is explained for the 24% silica-filled silicone, and only the final results for the other two materials are presented afterward.

The estimated relaxation modulus of this material found after the conversion of the storage and loss moduli as per Eq. 11 is plotted in Fig. 11. These relaxation data are applied for the parameter identification of Eq. 10. The fit is also plotted in Fig. 11, which demonstrates that the proposed function correctly reproduces the behavior of the material. The set of optimized values of the parameters \(G_{\infty }\), \(G_g\) and \(t_0\) is shown in Table 2.

Fig. 11
figure 11

Relaxation modulus for times between 0.016 and 16 s at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of 24% silica-filled silicone, estimated from Eq. 11, and fitted values as per Eq. 10

Full size image
Table 2 Parameters for aging-depend Maxwell model identification
Full size table

Following the previously described steps, after the parameter identification it is possible to find the continuous spectrum of relaxation times, which depends on the parameter \(\beta \) (and therefore on the aging parameters). The plots of H as function of the relaxation time for different aging conditions are shown in Fig. 12. The values reached by this function become higher as the parameter \(\beta \) increases.

Fig. 12
figure 12

Continuous spectrum of relaxation times for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of 24% silica-filled silicone

Full size image

Finally, all parameters of the aging-dependent Maxwell model are found thanks to a discretization of the relaxation times, and the application of Eqs. 7 and 17. The comparison between the experimental relaxation modulus for varying aging times and the identified Maxwell model is shown in Fig. 13. In this case, the space of relaxation times was discretized into \(n=21\) points with \(\tau _{min} = 10^{-4} s\) and \(\tau _{max} = 10^{25} s\). It is important to mention that values of minimum and maximum relaxation times take values well outside of the experimental range. The choice of such extreme values is necessary from a numerical point of view to obtain a correct fit of the material behavior for the whole data set, for different aging conditions.

Fig. 13
figure 13

Relaxation modulus for times between 0.016 and 16 s at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of 24% silica-filled silicone, estimated from Eq. 11, and comparison with identified aging-dependent Maxwell model

Full size image

This figure shows that the identified aging-dependent generalized Maxwell model accurately describes the changes in the mechanical properties of the studied material as aging progresses.

The final step for the postulation of an aging-dependent model is the proposition of a relation between the parameter \(\beta \) that has already been identified and the aging parameters \(\theta _a\) and \(t_a\). The phenomenological Eq. 18 is used to describe this relation.

$$\begin{aligned} \beta (\theta _a,t_a) = \beta _0 \cdot \left( 1 + \frac{t_a}{t_{a_0}} \right) ^{a \cdot \exp (b\,\theta _a)} \end{aligned}$$
(18)

The values of \(\beta \) for each pair of \((\theta _a,t_a)\) are presented in Fig. 14. It is possible to see that \(\beta \) increases with higher values of the aging parameters and that the proposed equation adequately captures the evolution of \(\beta \) as function of \(t_a\) and \(\theta _a\). The coefficients identified for the evolution of the parameter \(\beta \) are listed in Table 2.

Fig. 14
figure 14

Evolution of \(\beta \) as a function of aging parameters, and comparison with modeled values as per Eq. 18, for 24% silica-filled silicone

Full size image

The same identification procedure was applied to the other two filled silicones. A summary of the results for the identification of the model as well as the relation of \(\beta \) with the aging time and temperature is shown in Figs. 15 and 16. The identified parameters are summarized in Table 2. It is possible to see that the model accurately predicts the behavior of the 14 % silica-filled silicone, but lacks precision when it comes to the silver-filled one. While the results are encouraging, it is possible that the model needs modifications and extensions to be applicable for a diversity of other materials with different aging responses than those treated in this article.

Fig. 15
figure 15

Relaxation modulus for times between 0.016 and 16 s at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of 14% silica-filled silicone, estimated from Eq. 11, and comparison with identified aging-dependent Maxwell model. d Evolution of \(\beta \) as a function of aging parameters, and comparison with modeled values as per Eq. 18

Full size image
Fig. 16
figure 16

Relaxation modulus for times between 0.016 and 16 s at 25 \(^{\circ }\)C for different aging parameters (a \(\theta _a=150\) \(^{\circ }\)C, b \(\theta _a=180\) \(^{\circ }\)C, c \(\theta _a=210\) \(^{\circ }\)C) of silver-filled silicone, estimated from Eq. 11, and comparison with identified aging-dependent Maxwell model. d Evolution of \(\beta \) as a function of aging parameters, and comparison with modeled values as per Eq. 18

Full size image

5 Conclusions

This work presents a contribution to the experimental study and modeling of filled silicone elastomers after aging in a hermetic and initially inert atmosphere. Dynamic Mechanical Analysis tests in torsional mode allow to correctly capture the viscoelastic properties and provide some interesting results. Amplitude sweep tests allow to observe the appearance of a nonlinear behavior above a certain strain amplitude and the impact of the filler content to this non-linearity. It was possible to observe that the non-linearity occurs for strain amplitudes above 1 % for the silica-filled silicones and above 0.01 % for the silver-filled silicone.

The frequency sweep tests at ambient temperature allowed to compare different aging conditions and to show that the aging translates into a softening of the material, manifested by a decrease in the moduli measured by DMA. This behavior was correctly described by an aging-dependent generalized Maxwell model based on the proposition of a continuous relaxation spectrum depending on the aging parameters.