Global reliability sensitivity analysis index and its efficient numerical simulation solution in presence of both random and interval hybrid uncertainty

Abstract

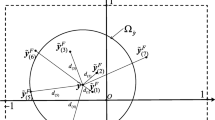
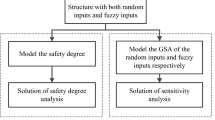
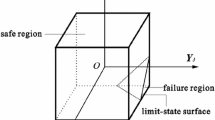
In the presence of both random and interval hybrid uncertainty (RI-HU), investigating global reliability sensitivity (GRS) can identify the effect of random input on the structural safety globally. To this end, this work establishes the GRS index model and its corresponding efficient solution, and the innovation includes three aspects. Firstly, the GRS of the random input is defined by the average absolute difference between the failure probability upper bound (FP-UB) and the conditional FP-UB on the fixed random input under the RI-HU, and it can reflect the effect of the fixed random input on the structural safety. Secondly, the conditional FP-UB on fixing the random input at the realization is approximated by the conditional FP-UB on fixing the random input in a differential interval. Then the conditional probability theorem can be employed to convert estimating the GRS into the state recognition of the samples, which is the by-product of estimating the FP-UB by the numerical simulation. Finally, by the strategy of surrogating the performance function twice, the meta-importance sampling method is developed to efficiently estimate the GRS in presence of the RI-HU. The rationality of the proposed GRS index model and the efficiency of the developed estimation method are fully verified by the numerical and engineering examples.

Appendix

1.1 SL-AK-MCS for GRS in presence of RI-HU

The basic idea of SL-AK-MCS is to build a single Kriging model to surrogate performance function with random and interval inputs directly. The strategy of constructing Kriging model to surrogate performance function in presence of RI-HU in SL-AK-MCS method is similar with the strategy of constructing ${g}_{K_2}\left(\boldsymbol{x},\boldsymbol{y}\right)$ listed in Subsection 3.2.2 of this work. The main implementation procedures of SL-AK-MCS for GRS in presence of RI-HU are summarized briefly as follows:

• (1) Construct the initial Kriging model g_K(x, y).

Generate N_x ‐ size sample pool ${S}_x=\left\{{x}_1,{x}_2,\dots, {x}_{N_x}\right\}$ according to the joint PDF f_X(x) of the random inputs and N_y ‐ size sample pool ${S}_y=\left\{{y}_1,{y}_2,\dots, {y}_{N_y}\right\}$ of interval variables according to y ∈ [y^L, y^U]. Randomly select N₁ training samples from S_x and S_y to constitute initial training samples $\left({\boldsymbol{x}}_k^T,{\boldsymbol{y}}_k^T\right)\left(k=1,2,\dots {N}_1\right)$; then compute the corresponding performance functions, and construct the initial training set $T=\left\{\Big(\left({x}_k^T,{y}_k^T\right),g\Big({x}_k^T,{y}_k^T\left)\right),k=1,2,\dots {N}_1\right\}$.

• (2) Select new training samples according to the criterions listed in Subsection 3.2.2 (2).

• (3) Judge the convergence of g_K(x, y) according to the criterions listed in Subsection 3.2.2 (3). When g_K(x, y) is convergent, turn to Step (4). Otherwise, turn to Step (2), and select new training samples to refine T to update g_K(x, y).

• (4) Estimate the FP-UB ${P}_f^U$ and obtain failure samples.

Predict the failure domain indicator function value ${\hat{I}}_{F_{\mathrm{min}}}\left({\boldsymbol{x}}_i\right)$ by (A1) at sample points x_i(i = 1, 2, …, N_x) in the sample pool S_x by the convergent g_K(x, y):

$$ {I}_{F_{\mathrm{min}}}\left(\boldsymbol{x}\right)=\left\{\begin{array}{c}0\kern0.5em \mathrm{if}\ \boldsymbol{x}\notin {F}_{\mathrm{min}}=\left\{\underset{y\in \left[{y}^L,{y}^U\right]}{\min }{g}_K\left(\boldsymbol{x},\boldsymbol{y}\right)\le 0\right\}\\ {}1\kern0.5em \mathrm{if}\ \boldsymbol{x}\in {F}_{\mathrm{min}}=\left\{\underset{y\in \left[{y}^L,{y}^U\right]}{\min }{g}_K\left(\boldsymbol{x},\boldsymbol{y}\right)\le 0\right\}\end{array}\right. $$

(A1)

Then the failure samples can be obtained, and the estimate ${\hat{P}}_f^U$ of ${P}_f^U$ can be estimated as follows:

$$ {\hat{P}}_f^U=\frac{1}{N_x}\sum \limits_{i=1}^{N_x}{\hat{I}}_{F_{\mathrm{min}}}\left({\boldsymbol{x}}_i\right) $$

(A2)

• (5) Estimate GRS in presence of RI-HU according to (18) using strategies revealed in Subsection 3.2.3.

1.2 DL-AK-MCS for GRS in presence of RI-HU

The DL-AK-MCS strategy builds two nested Kriging models to estimate the ${P}_f^U$ in the presence of RI-HU. In the inner loop, the Kriging model g_K(x^∗, y) surrogating the relation of performance function with respect to the interval inputs on the random input vector fixed at x^∗ is built, which is responsible for searching the minimum of performance function at the fixed random input x^∗. In the outer loop, the Kriging model G_eK(x) for the minimum surface G_e(x) = min {g(x, y), y ∈ [y^L, y^U]} should be built, which is a model respect to the random input vector and is used for reliability analysis. After the outer Kriging model is convergent, the FP-UB and failure samples can be obtained, and (18) can be used to estimate the GRS in presence of RI-HU. The main implementation procedures of DL-AK-MCS for GRS in presence of RI-HU are summarized as follows:

• (1) Generate N_x ‐ size sample pool ${S}_x=\left\{{x}_1,{x}_2,\dots, {x}_{N_x}\right\}$ according to the joint PDF f_X(x) of the random inputs. Randomly select ${N}_1^x$ random samples ${\boldsymbol{x}}_k^T\left(k=1,2,\dots {N}_1^x\right)$ from S_x as the initial training samples for the outer loop Kriging model.

• (2) Construct the inner loop Kriging model g_K(x^∗, y) at the fixed random input x^∗.

• 1) Generate sample pool ${S}_y=\left\{{y}_1,{y}_2,\dots, {y}_{N_y}\right\}$ of interval variables according to y ∈ [y^L, y^U]. Select ${N}_1^y$ samples ${\boldsymbol{y}}_k^T\left(k=1,2,\dots {N}_1^y\right)$ from S_y. Compute the actual performance function values $g\left({x}^{\ast },{y}_k^T\right)\left(k=1,\dots, {N}_1^y\right)$, and construct training set ${T}^y=\left\{\Big({y}_k^T,g\left({x}^{\ast },{y}_k^T\right)\Big),\Big(k=1,\dots, {N}_1^y\Big)\right\}$_.

• 2) Build the inner loop Kriging model g_K(x^∗, y) using training set T^y.

• 3) Estimate the expected maximum improvement E(I(y)) by (A3) for samples in S_y:

$$ E\left(I(y)\right)=E\left[\max \left({g}_K^{\mathrm{min}}\left({x}^{\ast}\right)-{g}_K\left({x}^{\ast },y\right),0\right)\right] $$

(A3)

where ${g}_K^{\mathrm{min}}\left({x}^{\ast}\right)=\underset{y\in \left[{y}^L,{y}^U\right]}{\min }{g}_K\left({x}^{\ast },y\right)$. The expected maximum improvement E(I(y)) is an extension of the one in Ref. (Wang and Wang 2015).

• 4) If $\underset{y\in {S}_y}{\max }E\left(I(y)\right)\ge {C}_B$ (C_B is the stopping condition corresponding to E(I(y)), which has been provided in Ref. (Wang and Wang 2015)), select the new training sample by ${y}^u=\arg \underset{y\in {S}_y}{\max }E\left(I(y)\right)$. Let ${T}^y=\left\{{T}^y\cup \Big({y}^u,g\left({x}^{\ast },{y}^u\right)\Big),\Big(k=1,\dots, {N}_1^y\Big)\right\}$, and return to Step (2). Otherwise, terminate updating the inner loop Kriging model, and go to Step (4).

• (4) Obtain ${G}_e\left({x}_k^T\right)=\underset{y\in \left[{y}^L,{y}^U\right]}{\min }{g}_K\left({x}_k^T,y\right)\left(k=1,2,\dots, {N}_1^x\right)$ using the inner loop Kriging model g_K(x^∗, y) obtained in Step (3). Let ${T}^x=\left\{\Big({x}_k^T,{G}_e\left({x}_k^T\right)\Big),\Big(k=1,\dots, {N}_1^x\Big)\right\}$.

• (5) Construct the outer loop Kriging model G_eK(x) by T^x.

• (6) Judge the convergence of G_eK(x)according to the criterions listed in Subsection 3.2.2 (3).

When the convergence criterion is satisfied, terminate the outer loop iteration and obtain the convergent G_eK(x); then go to Step (7). Otherwise, find the new training sample by ${x}^u=\arg \underset{x\in {S}_x}{\max }{C}_A(x)$, where C_A(x) is a learning function for the selection of samples proposed in Ref. (Wang and Wang 2015). Compute ${G}_e\left({x}^u\right)=\underset{y\in \left[{y}^L,{y}^U\right]}{\min }{g}_K\left({x}^u,y\right)$ by the inner loop Kriging model g_K(x^∗, y) obtained in Step (3). Let ${T}^x=\left\{{T}^x\cup \Big({x}^u,{G}_e\left({x}^u\right)\Big),\Big(k=1,\dots, {N}_1^x\Big)\right\}$, and go to Step (5).

• (7) Estimate ${P}_f^U$ using (A4) and obtained failure samples:

$$ {P}_f^U=\frac{1}{N_x}\sum \limits_{i=1}^{N_x}{I}_F\left({G}_{eK}\left({\boldsymbol{x}}_i\right)\right) $$

(A4)

where I_F(G_eK(x_i)) is the indicator function of failure domain F = {x : G_eK(x) ≤ 0}. If G_eK(x) ≤ 0, I_F(⋅) = 1. If G_eK(x) > 0, I_F(⋅) = 0..

• (8) Estimate GRS in presence of RI-HU according to (18) using strategies revealed in Subsection 3.2.3.