Multi-fidelity modeling with different input domain definitions using deep Gaussian processes

Abstract

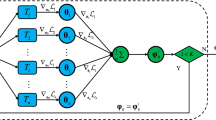
Multi-fidelity approaches combine different models built on a scarce but accurate dataset (high-fidelity dataset), and a large but approximate one (low-fidelity dataset) in order to improve the prediction accuracy. Gaussian processes (GPs) are one of the popular approaches to exhibit the correlations between these different fidelity levels. Deep Gaussian processes (DGPs) that are functional compositions of GPs have also been adapted to multi-fidelity using the multi-fidelity deep Gaussian process (MF-DGP) model. This model increases the expressive power compared to GPs by considering non-linear correlations between fidelities within a Bayesian framework. However, these multi-fidelity methods consider only the case where the inputs of the different fidelity models are defined over the same domain of definition (e.g., same variables, same dimensions). However, due to simplification in the modeling of the low fidelity, some variables may be omitted or a different parametrization may be used compared to the high-fidelity model. In this paper, deep Gaussian processes for multi-fidelity (MF-DGP) are extended to the case where a different parametrization is used for each fidelity. The performance of the proposed multi-fidelity modeling technique is assessed on analytical test cases and on structural and aerodynamic real physical problems.

Appendices

Appendix 1: Derivation of the evidence lower bound of MF-DGP-EM

By marginalizing the latent variable, the log evidence of the model $\log p\left (\{y^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s}|\{X^{t}\}_{t=1}^{s} \right )$ is given by:

$$ \begin{array}{ll} &\log p\left( \{\mathbf{y}^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s}|\{X^{t}\}_{t=1}^{s},\right) = \\ &\log \int\int\int\int p\left( \{y^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s} ,\mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}|\{X^{t}\}_{t=1}^{s} \right)\\& \mathrm{d}\mathcal{F}\mathrm{d}\mathcal{U}\mathrm{d}\mathcal{H}\mathrm{d}\mathcal{V} \end{array} $$

(30)

Then, the variational approximation used in (13) $q(\mathcal {F},\mathcal {U},$ ${\mathscr{H}},\mathcal {V})$ is introduced as follows:

$$ \begin{array}{ll} &\log p\left( \{\mathbf{y}^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s}|\{X^{t}\}_{t=1}^{s} \right) =\\ & \log \int\int\int\int p\left( \{\mathbf{y}^{t}\}_{t=1}^{s},\mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}|\{X^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s} \right) \\&\frac{q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right)}{q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right)}\mathrm{d}\mathcal{F}\mathrm{d}\mathcal{U}\mathrm{d}\mathcal{H}\mathrm{d}\mathcal{V} \end{array} $$

(31)

A lower bound on the log evidence of the model is obtained using Jensen inequality which relates a concave function of an integral (the logarithm in this case) to the concave function of the integral (Jensen et al. 1906):

$$ \begin{array}{ll} &\log p\left( \{\mathbf{y}^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s}|\{X^{t}\}_{t=1}^{s} \right) \geq \\ & \mathcal{L}= \int\int\int\int q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right) \times \\& \log \frac{p\left( \{\mathbf{y}^{t}\}_{t=1}^{s},\{X^{t}_{t-1}\}_{t=2}^{s},\mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}|\{X^{t}\}_{t=1}^{s}\right)}{q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right),}\\ &\mathrm{d}\mathcal{F}\mathrm{d}\mathcal{U}\mathrm{d}\mathcal{H}\mathrm{d}\mathcal{V} \end{array} $$

(32)

Then, by replacing the variational distribution by its expression in (13) and canceling out equivalent terms in the numerator and denominator, the following expression is obtained (the dependence on $\{X^{t}\}_{t=1}^{s}$ for notation simplicity) :

$$ \begin{array}{ll} &\mathcal{L} = \int\int\int\int q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right)\\ & \log\left( \frac{(p(\{\mathbf{y}^{t}\}_{t=1}^{s}|\mathcal{F})p(\{X^{t}_{t-1}\}_{t=2}^{s}|\mathcal{H}) \times p(\mathcal{U}) \times p(\mathcal{V})}{q(\mathcal{U}) \times q(\mathcal{V})}\right)\\ &\mathrm{d}\mathcal{F}\mathrm{d}\mathcal{U}\mathrm{d}\mathcal{H}\mathrm{d}\mathcal{V} \end{array} $$

(33)

Next, the $\log$ expression is separated into a sum of four terms:

$$ \begin{array}{ll} &\mathcal{L} = \int\int\int\int q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right) \log\left( p(\{\mathbf{y}^{t}\}|\mathcal{F})\right)+\\ & q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right) \log\left( p(\{X^{t}_{t-1}\}_{t=2}^{s})\right)+ \\ & q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right) \log \left( \frac{p(\mathcal{U})}{q(\mathcal{U})} \right)+\\ & q\left( \mathcal{F},\mathcal{U},\mathcal{H},\mathcal{V}\right) \log \left( \frac{p(\mathcal{V})}{q(\mathcal{V})} \right)\\ &\mathrm{d}\mathcal{F}\mathrm{d}\mathcal{U}\mathrm{d}\mathcal{H}\mathrm{d}\mathcal{V} \end{array} $$

(34)

The first term does not depend on the variables ${\mathscr{H}}, \mathcal {U}$, and $\mathcal {V}$; thus, it comes back to:

$$ \begin{array}{ll} \mathcal{L}_{1} = \int q\left( \mathcal{F}\right) \log\left( p(\{\mathbf{y}^{t}\}_{t=1}^{s}|\mathcal{F})\right)\mathrm{d}\mathcal{F} \end{array} $$

(35)

For the second term of the sum, the log expression does not depend on on the variables $\mathcal {F}, \mathcal {U}$, and $\mathcal {V}$; thus, the second term comes back to:

$$ \begin{array}{ll} \mathcal{L}_{2} = \int q\left( \mathcal{H}\right) \log\left( p(\{X^{t}_{t-1}\}_{t=2}^{s}|\mathcal{H})\right)\mathrm{d}\mathcal{H} \end{array} $$

(36)

For the third term, the log expression does not depend on on the variables $\mathcal {F}, {\mathscr{H}}$, and $\mathcal {V}$; thus, the third term comes back to:

$$ \begin{array}{ll} \mathcal{L}_{3} = \int q\left( \mathcal{U}\right)\log \left( \frac{p(\mathcal{U})}{q(\mathcal{U})} \right) \mathrm{d}\mathcal{U} \end{array} $$

(37)

For the fourth term, the log expression does not depend on on the variables $\mathcal {F}, {\mathscr{H}}$, and $\mathcal {U}$; thus, the fourth term comes back to:

$$ \begin{array}{ll} \mathcal{L}_{4} = \int q\left( \mathcal{V}\right)\log \left( \frac{p(\mathcal{V})}{q(\mathcal{V})} \right) \mathrm{d}\mathcal{V} \end{array} $$

(38)

By injecting these terms in (34) and identifying the expectation and KL divergence terms, then factorizing over the training dataset the final expression is obtained:

$$ \begin{array}{@{}rcl@{}} \mathcal{L}&=&\sum\limits_{t=1}^{s} \sum\limits_{i=1}^{n_{t}} \mathbb{E}_{q(f_{t}^{(i),t})} \left[\log p\left( y^{(i),t}|f_{t}^{(i),t}\right)\right] +\\ &&\sum\limits_{t=1}^{s-1} \sum\limits_{i=1}^{n_{t}} \mathbb{E}_{q(H_{t}^{(i),t+1})} \left[\log p\left( X^{(i),t+1}|H_{t}^{(i),t+1}\right)\right] - \\ && \sum\limits_{l=1}^{s} KL\left[q\left( \mathbf{u}_{l}\right)||p\left( \mathbf{u}_{l};Z_{l-1}\right)\right]-\\ && \sum\limits_{l=1}^{s-1} KL\left[q\left( V_{l}\right)||p\left( V_{l};Z_{l+1}\right)\right] \end{array} $$

(39)

Appendix 2: Training of MF-DGP-EM

The training of MF-DGP-EM comes back to the maximization of the ELBO. This maximization is performed with respect to the hyperparameters of the fidelities GPs $\{\theta \}_{l=1}^{s}$, the hyperparameters of the input mapping multi-output GPs $\{\theta _{\text {map}}\}_{l=1}^{s-1}$, the induced inputs $\{Z_{l}\}_{l=1}^{s}, \{W_{l}\}_{l=1}^{s-1}$, and also the variational parameters of the variational distributions $\{q(\mathbf {u}_{l})\}_{l=1}^{s},\{q(V_{l})\}_{l=1}^{s-1}$.

1.1 The variational variables

Including the variational distribution parameters makes the parameter space not Euclidian; hence, the ordinary gradient is not a suitable direction to follow (Amari and Douglas 1998). In fact, the variational distribution parameter space has a Riemannian structure defined by the Fisher information. In this case, the natural gradient which comes back to the ordinary gradient rescaled by the inverse Fisher information matrix is the steepest descent direction. This approach is used for MF-DGP-EM. Specifically, the optimization procedure consists of a loop between an optimization step using a stochastic ordinary gradient (Adam Optimizer (Kingma and Ba 2014)) with respect to the Euclidian space parameters and an optimization step using the natural gradient with respect to all the variational parameters of the variational distributions.

1.2 The induced inputs

One of the major difficulties in MF-DGP is the optimization of the inducing inputs $\{Z_{l}\}_{l=1}^{s}$. In Cutajar et al. (2019), the inducing inputs were arbitrary fixed and not optimized. In fact, except for the first layer, the inducing inputs in MF-DGP do not play the same role as in classic DGPs, where they are defined in the original input space. Specifically, the input space of the inner layers of the MF-DGP is augmented with the output of the previous layer, inducing a non-linear dependence between the d first components and the d + 1 component of each element in this augmented input space. In fact, due to the dependence between the d first components and the d + 1 component of each induced variable, freely optimizing Z_l (with 2 ≤ l ≤ s) as vectors with independent components is no longer suitable.

To overcome this issue in MF-DGP-EM, $\{Z_{l}\}_{l=2}^{s}$ are constrained as follows:

$$ Z_{l} = \left[Z_{l,1:d},f^{*}_{l-1}\left( H^{*}_{l-1}(Z_{l,1:d})\right)\right] ; \forall 2\leq l\leq s $$

(40)

where $f^{*}_{l-1}(\cdot )$ corresponds to the posterior mean prediction at the previous layer and $H^{*}_{l-1}(\cdot )$ to the mean mapped value into the lower fidelity. This constraint keeps a dependency between Z_l,d+ 1 and Z_l,1:d, allowing to remove Z_l,d+ 1 from the expression of the ELBO. Hence, the optimization is done with respect to Z_l,1:d instead of Z_l.

Appendix 3: Numerical setup

• All experiments were executed on Grid’5000 using a Tesla P100 GPU. The code is based on GPflow (Matthews et al. 2017), Doubly-Stochastic-DGP (Salimbeni and Deisenroth 2017), and emukit (Paleyes et al. 2019).

• For all GPs, Automatic Relevance Determination (ARD) Squared Exponential (SE) kernels are used with a length scale and variance initialized to 1. The data is scaled so the HF data have a zero mean and a variance equal to 1.

• The Adam optimizer is set with β₁ = 0.9 and β₂ = 0.99 and a step size γ^adam = 0.003.

• The natural gradient step size is initialized for all layers at γ^nat = 0.01

• The number of training iterations for MF-DGP-EM is fixed to 28,000 iterations (one iteration = Adam step + natural gradient step).

• The mean of the variational distribution of the inducing variables for the layer t is initialized at y^t, and for the input mapping GP at layer t at $X^{t+1}_{t}$.

• The inducing input of the fidelity GP at layer t is initialized at X^t, and for the input mapping GP at layer t it is initialized at X^t+ 1.

• A Github repository featuring MF-DGP-EM will be available after the publication of the paper.

Appendix 4: Numerical results

Table 2 Performance of the different multi-fidelity models on problem 1 (21 and 22) using 20 repetitions with different LHS generated DoE

Table 3 Performance of the different multi-fidelity models on problem 2 (24 and 25) using 20 repetitions with different LHS generated DoE

Table 4 Performance of the different multi-fidelity models on the structural problem (Section 4.2) using 20 repetitions with different LHS generated DoE

Table 5 Performance of the different multi-fidelity models on the aerodynamic problem (Section 4.3) using 20 repetitions with different LHS generated DoE