1 Introduction

Metamodels are frequently used to represent the responses of numerical simulations using less computationally expensive mathematical models. The reader is referred to Barthelemy and Haftka (1993), Wang and Shan (2007), Forrester and Keane (2009), and Viana et al. (2014, 2010) for reviews on metamodel-based optimisation in general.

This paper is concerned with Kriging which is an interpolating metamodelling technique based on spatial correlation that was first proposed by Krige (1951) and later implemented by Matheron (1963) for use within the mining industry. The use of Kriging for replacing expensive computational models with metamodels was shown by Sacks et al. (1989).

In many simulation software products derivatives with respect to the design variables, hereafter referred to as design sensitivities, can be cost efficiently obtained using for instance the adjoint method. The reader is referred to Martins and Hwang (2013) for a review on obtaining design sensitivities. If design sensitivities are available, these can be incorporated into the Kriging equations in order to enhance the metamodel quality (Han et al. 2013; Zimmermann 2013; Kim and Lee 2010). This is commonly known as gradient enhanced kriging (GEK). One of the main challenges of kriging, and gradient enhanced kriging in particular, is the computational cost associated with building the metamodel. This requires optimisation of a condensed log likelihood function with respect to a set of hyper-parameters, one for each design variable. Every evaluation of the condensed log likelihood function requires decomposition of a square correlation matrix, \(\textbf {R} \in \mathbb {R}^{d \times d}\). For kriging d = p, where p is the number of training points, and for gradient enhanced kriging d = p×(n+1) where n is the number of design variables. For problems with a small number of design variables, gradient based algorithms such as sequential quadratic programming have shown good performance (Zimmermann 2013; Lockwood and Anitescu 2010). To increase the probability of finding a better solution for problem with several optima, multiple start-points have also been proposed, with as few as five points (Lockwood and Anitescu 2010) or as many ten times the number of hyper-parameters (Liu and Batill 2002). For larger problems the optimisation is often carried out using global algorithms such as simulated annealing (Xiong et al. 2007) and genetic algorithm (Forrester et al. 2008). Toal et al. (2011) proposed a Hybrid optimisation scheme where promising points from a particle swarm optimisation were used as starting points for gradient based optimisations using sequential quadratic programming. In the same paper it was also shown how the adjoint method can be used to obtain partial derivatives of the condensed log likelihood function with respect to the correlation matrix, which greatly reduces the computational effort required when compared to finite differences and the direct method.

Ill-conditioning of the correlation matrix can become an issue when building metamodels where training points are located near each other (Haaland et al. 2011), especially for Gaussian correlation matrices (Zimmermann 2015). Attempts have been made to reduce ill conditioning by, for instance, using uniform subsets of the training points Rennen (2008), adding regularisation terms along the diagonal of the correlation matrix which makes the kriging metamodel approximate rather than interpolate the data, and constraining the condition number explicitly during optimisation Dalbey (2013).

In this paper partial derivatives of the condition number of the correlation matrix with respect to the hyper-parameters are obtained making it possible to constrain the condition number directly in a gradient based optimisation approach. A two-step approach is suggested for optimisation of the hyper parameters. In the first step, the optimisation problem is considered as a single variable problem by treating all hyper parameters as one variable. The solution to this problem is then used as a starting point for a gradient based optimisation algorithm. In both cases an upper bound constraint is enforced on the condition number of the correlation matrix. The approach is tested on several analytical examples using two types of gradient based optimisation algorithms, the sequential quadratic programming and the method of feasible directions. The approach is compared to gradient based optimisations starting from random points, multiple starting points and, a genetic algorithm followed by gradient based optimisations. Finally a case study is presented where the responses of an aircraft wing-box with 126 design variables is approximated using the suggested approach and compared to a selection of optimisation methods.

2 Kriging

Kriging is an interpolating metamodel technique based on spatial correlation that was first proposed by Krige (1951) and later implemented by Matheron (1963) for use within the mining industry. The use of kriging for approximation of expensive computational models was shown by Sacks et al. (1989).

Following the notation of Jones (2001), kriging is derived from the assumption that computer simulations are entirely deterministic and any error in the fit of a metamodel is entirely down to missing terms in the model. Given a set of p training points \(\textbf {x}^{(i)} \in \mathbb {R}^{n}\), i = 1,p and the corresponding function values y (i), i = 1,p, the kriging model can in general be written as

$$ \hat{y}(\textbf{x}) = \sum\limits_{j=1}^{h} b_{j}(\textbf{x})a_{j} + \hat\epsilon(\textbf{x}) $$
(1)

where b j (x) is the j-th regressor, a j the corresponding regression coefficient, and \(\hat \epsilon _{i}(\textbf {x})\) is the model of the error in the weighted least squares fit. It is assumed that the error, 𝜖 i (x), is continuous for any continuous function y(x), and that the error at two points 𝜖(x (i)) and 𝜖(x (j)) are correlated with their distance according to some model ψ(x (i),x (j)). As the error is modelled explicitly in kriging, the model will exactly interpolate through the training points.

The first part of the model (1), the polynomial regression, can be of arbitrary order, however the order of the regression model will dictate the number of required points which must be at least as many as the number of regressors. Kriging with zero-th order polynomials is usually referred to as ordinary kriging while using first or higher order polynomials are denoted universal kriging. In this work, ordinary kriging is used. The model for ordinary kriging, hereafter referred to as kriging, takes the form

$$ \hat{y}(\textbf{x}) = \hat{\mu} + \hat\epsilon(\textbf{x}) $$
(2)

where the estimated mean \(\hat {\mu }\) is determined by solving the weighted least squares problem

$$ \hat{\mu} = \left( \textbf{F}^{T}\textbf{R}^{-1}\textbf{F}\right)^{-1} \textbf{F}^{T}\textbf{R}^{-1}\textbf{y}, $$
(3)

and F is a matrix of regressors, representing a zero-th order basis function in ordinary kriging, is reduced to a vector of ones according to

$$ \mathbf{F}=\boldsymbol{1}=[\underset{\mathrm{p}}{\underbrace{1,...,1}}]^{T}. $$
(4)

The correlation matrix, R, contains the estimated spatial correlation between all the training points

$$ \textbf{R}=\left[\begin{array}{ccc} \psi(\textbf{x}^{(1)},\textbf{x}^{(1)})&\hdots&\psi(\textbf{x}^{(1)},\textbf{x}^{(p)}) \\ \vdots&\ddots&\vdots\\ \psi(\textbf{x}^{(p)},\textbf{x}^{(1)})&\hdots&\psi(\textbf{x}^{(p)},\textbf{x}^{(p)}) \end{array}\right] $$
(5)

here modelled as a Gaussian function according to

$$ \psi(\textbf{x}^{(i)},\textbf{x}^{(j)}) = exp{\left[ \sum\limits_{k=1}^{n} -\theta_{k} \left( \left|\left|\textbf{x}_{k}^{(i)}-\textbf{x}_{k}^{(j)}\right|\right|\right)^{2} \right]}, $$
(6)

where 𝜃 k is a so called hyper-parameter that scales the influence of the k-th design variable. The value of 𝜃 k is obtained through optimisation and will be discussed in Section 5. The second part of (2), the error \(\hat \epsilon (\textbf {x})\), treated as a stochastic process, is modelled as

$$ \hat\epsilon(\textbf{x}) = \textbf{w}^{T}\textbf{r}(\textbf{x}) $$
(7)

where r contains basis functions depending on the spatial correlation model (6) between the evaluation point, x (e), and the training points

$$ \textbf{r}=\left[\psi(\textbf{x}^{(e)},\textbf{x}^{(1)}), ...,\psi(\textbf{x}^{(e)},\textbf{x}^{(p)})\right]^{T}, $$
(8)

and corresponding weights, w, obtained through solving the linear equation system

$$ \textbf{w}=\textbf{R}^{-1}\left( \textbf{y}-\textbf{F}\hat{\mu}\right). $$
(9)

The final predicted kriging predictor is given by

$$ \hat{y}(\textbf{x}^{(e)}) = \hat{\mu} + \textbf{w}^{T}\textbf{r}, $$
(10)

and a predicted mean squared error of the kriging predictor is obtained as

$$ s^{2}(\textbf{x}^{(e)}) = \hat{\sigma}^{2} \left[ 1-\textbf{r}^{T}\textbf{R}^{-1}\textbf{r}+\frac{(1-\textbf{F}^{T}\textbf{R}^{-1}\textbf{r})^{2}}{\textbf{F}^{T}\textbf{R}^{-1}\textbf{F}} \right], $$
(11)

where \(\hat {\sigma }\) is the predicted system variance

$$ \hat{\sigma}^{2} = \frac{1}{p}\left( \textbf{y}-\textbf{F}\mu\right)^{T}\textbf{R}^{-1}\left( \textbf{y}-\textbf{F}\mu\right). $$
(12)

It should be noted that in order to solve the systems of linear equations in (3), (9), (11) and (12) Cholesky decomposition (DPOTRF) and back substitution (DPOTRS) routines from the Intel Math Kernel Library 11.2 (Intel 2015) was used.

3 Gradient-enhanced kriging

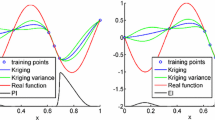
If, in addition to function values, design sensitivities are available they may be used to improve the accuracy of the kriging metamodel. The method of incorporating gradients in kriging is commonly referred to as gradient enhanced kriging (GEK) and is described in this section. Figure 1 shows an example of a kriging and gradient enhanced kriging fit respectively for a one dimensional function. It is clear that the gradient enhanced fit is of superior quality. The presented implementation is inspired by Han et al. (2013) and Lockwood and Anitescu (2010) to which the reader is referred for further information. In order to create a gradient enhanced kriging fit the correlation matrix is extended to include derivative terms according to

$$ \textbf{R}=\left[\begin{array}{cccc} \textbf{Q}^{1,1}&Q^{1,2}\\ (\textbf{Q}^{1,2})^{T}&\textbf{Q}^{2,2} \end{array}\right]. $$
(13)

where Q 1,1 is the correlation matrix used in the non-gradient case

$$ \textbf{Q}^{1,1}=\left[\begin{array}{ccc} \psi(\textbf{x}^{(1)},\textbf{x}^{(1)})&\hdots&\psi(\textbf{x}^{(1)},\textbf{x}^{(p)}) \\ \vdots&\ddots&\vdots\\ \psi(\textbf{x}^{(p)},\textbf{x}^{(1)})&\hdots&\psi(\textbf{x}^{(p)},\textbf{x}^{(p)}) \end{array}\right], $$
(14)

Q 1,2 contains the first derivatives of R according to

$$ \textbf{Q}^{1,2}=\left[\begin{array}{ccc} \frac{\partial \psi(\textbf{x}^{(1)},\textbf{x}^{(1)})}{\partial \textbf{x}^{(1)}}&\hdots&\frac{\partial \psi(\textbf{x}^{(1)},\textbf{x}^{(p)})}{\partial \textbf{x}^{(p)}}\\ \vdots&\ddots&\vdots\\ \frac{\partial \psi(\textbf{x}^{(p)},\textbf{x}^{(1)})}{\partial \textbf{x}^{(1)}}&\hdots&\frac{\partial \psi(\textbf{x}^{(p)}\textbf{x}^{(p)})}{\partial \textbf{x}^{(p)}} \end{array}\right], $$
(15)

where

$$ \frac{\partial \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial \textbf{x}^{(j)}} = \left[ \begin{array}{c} \frac{\partial \psi(\textbf{x}^{(i)},\textbf{x}^{(i)})}{\partial x^{(j)}_{1}} \hdots \frac{\partial \psi(\textbf{x}^{(i)},\textbf{x}^{(i)})}{\partial x^{(j)}_{n}} \end{array} \right]. $$
(16)

and, using the Gaussian function in (6)

$$ \frac{\partial \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial x^{(j)}_{k}} = 2\theta_{k}\left( x^{(i)}_{k}-x^{(j)}_{k}\right) \psi\left( \textbf{x}^{(i)}_{k},\textbf{x}^{(j)}_{k}\right). $$
(17)

The sub-matrix Q 2,2 contains the second derivatives

$$ \textbf{Q}^{2,2}=\left[\begin{array}{ccc} \frac{\partial^{2} \psi(\textbf{x}^{(1)},\textbf{x}^{(1)})}{\partial\textbf{x}^{(1)} \partial\textbf{x}^{(1)}}&\hdots&\frac{\partial^{2} \psi(\textbf{x}^{(1)},\textbf{x}^{(p)})}{\partial\textbf{x}^{(1)} d\textbf{x}^{(p)}} \\ \vdots&\ddots&\vdots\\ \frac{\partial^{2} \psi(\textbf{x}^{(p)},\textbf{x}^{(1)})}{\partial\textbf{x}^{(p)} \partial\textbf{x}^{(1)}}&\hdots&\frac{\partial^{2} \psi(\textbf{x}^{(p)}\textbf{x}^{(p)})}{\partial\textbf{x}^{(p)} \partial\textbf{x}^{(p)}} \end{array}\right], $$
(18)

where

$$ \frac{\partial^{2} \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial\textbf{x}^{(i)} \partial\textbf{x}^{(j)}} = \left[\begin{array}{ccc} \frac{\partial^{2} \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial x_{1}^{(i)}\partial x_{1}^{(j)}} & \hdots &\frac{\partial^{2} \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial x_{n}^{(i)}\partial x_{1}^{(j)}} \\ \vdots&\ddots&\vdots\\ \frac{\partial^{2} \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial x_{1}^{(i)}\partial x_{n}^{(j)}} & \hdots &\frac{\partial^{2} \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial x_{n}^{(i)}\partial x_{n}^{(j)}} \end{array}\right], $$
(19)

and, using the Gaussian function in (6)

$$ \begin{array}{lll} &\frac{\partial^{2} \psi(\textbf{x}^{(i)},\textbf{x}^{(j)})}{\partial x_{l}^{(i)} \partial x_{k}^{(j)}} = \\ &\left\{\begin{array}{llll} 2\theta_{k}\left[-2\theta_{k}\left( x_{k}^{(i)}-x_{k}^{(j)}\right)^{2} +1\right]\psi(\textbf{x}^{(i)},\textbf{x}^{(j)}) & \text{ , \(k = l\)}\\ -4\theta_{k}\theta_{l} \left[\left( x_{k}^{(i)}-x_{k}^{(j)}\right)\left( x_{l}^{(i)}-x_{l}^{(j)}\right)\right] \psi(\textbf{x}^{(i)},\textbf{x}^{(j)}) & \text{ , \(k \neq l\)} \end{array}\right. \end{array} $$
(20)

The vector of spatial correlations between the evaluation points and the training points is extended in the same manner to

$$ \textbf{r}= \left[ \begin{array}{c} \psi(\textbf{x}^{(e)},\textbf{x}^{(1)})\\ \vdots\\ \psi(\textbf{x}^{(e)},\textbf{x}^{(p)})\\ \frac{\partial \psi(\textbf{x}^{(e)},\textbf{x}^{(p)})}{\partial \textbf{x}^{(1)}}\\ \vdots\\ \frac{\partial \psi(\textbf{x}^{(e)},\textbf{x}^{(p)})}{\partial \textbf{x}^{(p)}}\\ \end{array} \right], $$
(21)

using the expression in (17). The vector of function values is extended to include design sensitivities as well as the function values

$$ \textbf{y} = \left[ \begin{array}{c} f(\textbf{x}^{(1)})\\ \vdots\\ f(\textbf{x}^{(p)})\\ \frac{\partial f(\textbf{x}^{(1)})}{\partial \textbf{x}}\\ \vdots\\ \frac{\partial f(\textbf{x}^{(p)})}{\partial \textbf{x}} \end{array} \right], $$
(22)

where

$$ \frac{\partial f(\textbf{x}^{(i)})}{\partial \textbf{x}} = \left[ \begin{array}{c} \frac{\partial f(\textbf{x}^{(i)})}{\partial x_{1}}\\ {\vdots} \\ \frac{\partial f(\textbf{x}^{(i)})}{\partial x_{n}}\\ \end{array} \\ \right]. $$
(23)

Similarly, the basis polynomial vector is extended to include the derivatives of the regression basis function. In the case of a zero-th order basis function, a vector of zeroes according to

$$ \textbf{F}= \begin{array}{llll} [& \textbf{1} & \textbf{0}] \end{array} =[\underbrace{1,...,1}_{\text{p}},\underbrace{0, ...,0}_{\text{p \(\times\) n}}]^{T}. $$
(24)

recalling that n is the number of design variables and p is the number of training points. The predicted mean is calculated as

$$ \hat{\mu} = \left( \textbf{F}^{T}\textbf{R}^{-1}\textbf{F}\right)^{-1} \textbf{F}^{T}\textbf{R}^{-1}\textbf{y}, $$
(25)

and the weights vector takes the form

$$ \textbf{w}=\textbf{R}^{-1}\left( \textbf{y}-\textbf{F}\hat{\mu}\right). $$
(26)

The final predicted kriging estimation at a point x (e) is calculated as

$$ \begin{array}{llll} \hat{y}(\textbf{x}^{(e)}) = \hat{\mu} + \textbf{w}^{T}\textbf{r} \end{array} $$
(27)

and a predicted mean squared error of the kriging prediction is given by

$$ s^{2}(\textbf{x}^{(e)}) = \hat{\sigma}^{2} \left[ 1-\textbf{r}^{T}\textbf{R}^{-1}\textbf{r}+\frac{(1-\textbf{F}^{T}\textbf{R}^{-1}\textbf{r})^{2}}{\textbf{F}^{T}\textbf{R}^{-1}\textbf{F}} \right], $$
(28)

where the predicted system variance is obtained as

$$ \hat{\sigma}^{2} = \frac{1}{n(1 + p)}\left( \textbf{y}-\textbf{F}\mu\right)^{T}\textbf{R}^{-1}\left( \textbf{y}-\textbf{F}\mu\right). $$
(29)
Fig. 1
figure 1

Kriging fit in one dimension. Gradient enhanced kriging significantly improves quality of fit

Full size image

It should be noted that in order to solve the systems of linear equations in (25), (26), (28) and (29) Cholesky decomposition (DPOTRF) and back substitution (DPOTRS) routines from the Intel Math Kernel Library 11.2 (Intel 2015) was used.

4 Noise regularisation

Although kriging is an interpolation technique it is possible to create a regression-like metamodel through regularisation as shown by Forrester et al. (2006). This is performed by adding a regularisation parameter to the diagonal elements of the correlation matrix according to

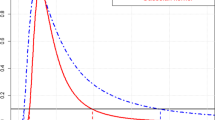
$$ \begin{array}{llll} &\textbf{R}= \textbf{R} + \lambda\textbf{I},& \lambda > 0, \end{array} $$
(30)

where λ is the regularisation parameter. The higher the value of lambda the more the metamodel is allowed to deviate from the training points. This is demonstrated in Fig. 2 which shows a one-dimensional fit of a noisy function with and without regularisation. It can be seen that the regularisation smooths the noisy function. Adding a regularisation parameter has an added benefit of improving the conditioning of the kriging equation system.

Fig. 2
figure 2

Kriging approximation of a noisy function

Full size image

For the gradient-enhanced case there is a possibility of noise in both the function values and the gradients values. As such it is beneficial to have two regularisation parameters, as proposed by Lukaczyk et al. (2013), one relating to the function values and one for the gradients. This leads to an augmentation of the correlation matrix according to

$$ \textbf{R}=\left[\begin{array}{cc} \textbf{Q}^{1,1}&Q^{1,2}\\ (\textbf{Q}^{1,2})^{T}&\textbf{Q}^{2,2} \end{array}\right] + \left[\begin{array}{cc} \lambda_{1}\textbf{I} & \quad\textbf{0} \\ \quad\textbf{0} & \lambda_{2}\textbf{I} \end{array} \right]. $$
(31)

By having two regularisation parameters, the regularisation of noisy function values and gradients can be addressed separately.

5 Hyper-parameter tuning

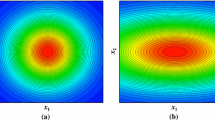
To obtain a good kriging fit it is important to determine suitable values of the hyper-parameters. Failing to do so may result in a sub-standard fit. Figure 3 shows an example of (a) an overestimated hyper parameter and (b) an optimised hyper parameter.

The hyper-parameters are determined through maximisation of the condensed log likelihood function (Jones 2001)

$$ \phi(\boldsymbol\theta) = -\frac{p}{2} \ln(\hat{\sigma}^{2}\left( \boldsymbol\theta\right)) -\frac{1}{2}\ln(|\textbf{R}(\boldsymbol\theta)|), $$
(32)

and for the gradient enhanced case (Han et al. 2013)

$$ \phi(\boldsymbol\theta) = -\frac{p(n+1)}{2} \ln(\hat{\sigma}^{2}\left( \boldsymbol\theta\right))-\frac{1}{2}\ln(|\textbf{R}(\boldsymbol\theta)|), $$
(33)

where |R(𝜃)| denotes the determinant of the correlation matrix. To prevent ill conditioning of the correlation matrix the condition number is constrained to be lower than some threshold during optimisation. The condition number is obtained as

$$ k(\textbf{R}) = \|\textbf{R}^{-1}\| \|\textbf{R}\|. $$
(34)

where ∥R∥ denotes the norm of the correlation matrix which is here calculated as the Frobenius norm

$$ \|\textbf{R}\| = \|\textbf{R}\|_{F} =\sqrt{\sum\limits_{i}\sum\limits_{j} R_{i,j}^{2}}. $$
(35)

and ∥R −1∥ denotes the norm of the inverse correlation matrix which is calculated using the matrix inversion (DPOTRI) routine from the Intel Math Kernel Library 11.2 (Intel 2015) using the matrix decomposition previously obtained for Kriging. Formally, the hyper-parameter optimisation problem takes the form

$$ \begin{array}{llll} & \underset{\boldsymbol\theta,\boldsymbol\lambda}{\text{maximise}} & & \phi(\boldsymbol\theta,\boldsymbol\lambda) \\ & \text{subject to} & & \kappa(\textbf{R}(\boldsymbol\theta,\boldsymbol\lambda)) \leq \kappa_{max} \\ \end{array} $$
(36)

where κ m a x is the upper bound constraint on the condition number. Here, κ m a x = 107 is used.

Fig. 3
figure 3

Importance of hyper-parameter optimisation

Full size image

Because of the computational expense related to hyper parameter optimisation this work is concerned with hyper parameter optimisation using gradient based optimisation techniques. In the following section it is shown how to obtain the gradients of the condensed log likelihood function and of the condition number with respect to the hyper parameters and regularisation parameters. These are then used for a hyper parameter optimisation approach outlined in the subsequent section.

6 Obtaining gradients

In order to use gradient based optimisation techniques, the gradients of the response functions are required. These can be obtained using different methods, with varying associated computational cost, depending on the problem at hand. For a large number of design variables, it may be prohibitively expensive to use finite differences or the direct method as the cost is proportional to the number of design variables. The computational cost of the adjoint method, however, is proportional to the number of response functions, which in this case are two, the condensed likelihood function and the condition number.

Using the chain rule the gradients of the condensed likelihood function with respect to the hyper parameters can be written as

$$ \frac{\partial \phi}{\partial\boldsymbol\theta} = \sum\limits_{i=1}^{p}\sum\limits_{j=1}^{p} \frac{\partial \phi}{\partial R_{ij}} \frac{\partial R_{ij}}{\partial\boldsymbol\theta} $$
(37)

and with respect to the regularisation parameters

$$ \frac{\partial \phi}{\partial\boldsymbol\lambda} = \sum\limits_{i=1}^{p}\sum\limits_{j=1}^{p} \frac{\partial \phi}{\partial R_{ij}} \frac{\partial R_{ij}}{\partial\boldsymbol\lambda}. $$
(38)

Similarly the gradients of the condition number with respect to the hyper parameters can be written as

$$ \frac{\partial \kappa}{\partial\boldsymbol\theta} = \sum\limits_{i=1}^{p}\sum\limits_{j=1}^{p} \frac{\partial \kappa}{\partial R_{ij}} \frac{\partial R_{ij}}{\partial\boldsymbol\theta} $$
(39)

and with respect to the regularisation parameters

$$ \frac{\partial \kappa}{\partial\boldsymbol\lambda} = \sum\limits_{i=1}^{p}\sum\limits_{j=1}^{p} \frac{\partial \kappa}{\partial R_{ij}} \frac{\partial R_{ij}}{\partial\boldsymbol\lambda} $$
(40)

In total there are four types of derivatives to establish. The gradients of the condensed likelihood function with respect to the correlation matrix, the gradients of the condition number with respect to the correlation matrix, and the gradients of the correlation matrix with respect to the hyper parameters and regularisation parameters. These are discussed in the following sections.

6.1 Gradients of the condensed likelihood function w.r.t. the correlation matrix

The partial derivatives of the condensed likelihood function with respect to the correlation matrix can be obtained using the adjoint method as shown by Toal et al. (2009) according to

$$ \begin{array}{lll} \frac{\partial \phi}{\partial\textbf{R}} = \bar{\textbf{R}}= \frac{1}{2\hat{\sigma}^{2}} \textbf{R}^{-T} \left( \textbf{y}-\textbf{F}\hat{\mu}\right) \left( \textbf{y}-\textbf{F}\hat{\mu}\right)^{T} \textbf{R}^{-T} -\frac{1}{2}\textbf{R}^{-T}. \end{array} $$
(41)

where \(\bar {\textbf {R}}\) is the adjoint of the correlation matrix. This is applicable to both the non-gradient and gradient-enhanced case.

6.2 Gradients of the condition number w.r.t. the correlation matrix

The adjoint method can also be used for obtaining gradients of the condition number with respect to the correlation matrix. Using the chain rule and recalling (34) the derivatives of the condition number with respect to the correlation matrix can be written as

$$ \frac{\partial\kappa}{\partial\textbf{R}} = \frac{\partial \|\textbf{R}^{-1}\|\|\textbf{R}\|}{\partial\textbf{R}} = \frac{\partial\|\textbf{R}\|}{\partial\textbf{R}}\|\textbf{R}^{-1}\| + \frac{\partial \|\textbf{R}^{-1}\|}{\partial\textbf{R}}\|\textbf{R}\| $$
(42)

With this result the intermediate variables for reversed differentiation of the condition number with respect to the correlation matrix can be determined. The intermediate variable for the first term can, given that the intermediate variable for the condition number itself has been initialised to \(\bar {\kappa }=1\), be written as

$$ \overline{\|\textbf{R}\|} = \bar{\kappa} \|\textbf{R}^{-1}\| = \|\textbf{R}^{-1}\|. $$
(43)

Using the results presented by Giles (2008) which are based on the work of Dwyer and MacPhail (1948) the adjoint of the Frobenius norm can be determined according to

$$ \overline{\textbf{R}} = \overline{\|\textbf{R}\|} \frac{1}{\|\textbf{R}\|} \textbf{R} $$
(44)

which together with (43) leads to the adjoint of the correlation matrix for the first term in (42)

$$ \overline{\textbf{R}}_{1} = \frac{\|\textbf{R}^{-1}\|}{\|\textbf{R}\|} \textbf{R}. $$
(45)

In the second term the intermediate variable from the product rule can be obtained as

$$ \overline{\|\textbf{R}^{-1}\|} = \bar{\kappa} \|\textbf{R}\| = \|\textbf{R}\| $$
(46)

Again, using the adjoint of the Frobenius norm leads to

$$ \overline{\textbf{R}^{-1}} = \overline{\|\textbf{R}^{-1}\|} \frac{1}{\|\textbf{R}^{-1}\|} \textbf{R}^{-1}. $$
(47)

Giles (2008) also presents the Adjoint of the inverse as

$$ \overline{\textbf{R}} = -\textbf{R}^{-T}\overline{\textbf{R}^{-1}}\textbf{R}^{-T} $$
(48)

which together with (47) and (46) leads to the adjoint of the correlation matrix for the second term in (42)

$$ \overline{\textbf{R}}_{2} = -\textbf{R}^{-T} \frac{\|\textbf{R}\|}{\|\textbf{R}^{-1}\|} \textbf{R}^{-1}\textbf{R}^{-T} $$
(49)

Adding (45) and (49) yields the gradients of the condition number with respect to the hyper parameters as

$$ \frac{\partial\kappa}{\partial\textbf{R}} = \overline{\textbf{R}}_{1} + \overline{\textbf{R}}_{2} = \frac{\|\textbf{R}^{-1}\|}{\|\textbf{R}\|} \textbf{R} - \frac{|\textbf{R}\|}{\|\textbf{R}^{-1}\|}\left( \textbf{R}^{-T}\ \textbf{R}^{-1}\textbf{R}^{-T}\right), $$
(50)

which is applicable both for the non-gradient and gradient-enhanced case.

6.3 Gradients of the correlation matrix w.r.t. regularisation parameters

The gradients of the correlation matrix with respect to the regularisation parameters can easily be obtained from (30) for the non-gradient case as

$$ \frac{\partial R}{\partial\lambda} = \textbf{I}_{p} $$
(51)

where \(\textbf {I}_{p} \in \mathbb {R}^{p \times p}\), is the identity matrix with the number of diagonal elements of p. For the gradient-enhanced case from (31), for the first regularisation parameter as

$$ \frac{\partial R}{\partial\lambda_{1}} = \left[\begin{array}{cc} \textbf{I}_{p} & \textbf{0} \\ \textbf{0} & \textbf{0} \end{array} \right] $$
(52)

and for the second regularisation parameter as

$$ \frac{\partial R}{\partial\lambda_{2}} = \left[\begin{array}{cc} \textbf{0} & \textbf{0} \\ \textbf{0} & \textbf{I}_{d} \end{array} \right] $$
(53)

where d = p×n.

6.4 Gradients of the correlation matrix w.r.t. the hyper parameters

For the non-gradient case, the partial derivatives of the correlation matrix with respect to the hyper parameters can be calculated as

$$ \frac{\partial R_{i,j}}{\partial\theta_{m}} = -\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2} R_{i,j}. $$
(54)

For the gradient enhanced case they can be calculated as

$$ \begin{array}{ccccc} \frac{\partial \textbf{R}}{\partial\theta_{m}} = \left[\begin{array}{ccc} \frac{\partial \textbf{Q}^{1,1}}{\partial\theta_{m}} &\frac{\partial \textbf{Q}^{1,2}}{\partial\theta_{m}} \\ \frac{\partial (\textbf{Q}^{1,2})^{T}}{\partial\theta_{m}} & \frac{\partial \textbf{Q}^{2,2}}{\partial\theta_{m}} \end{array}\right] \end{array}. $$
(55)

where the first quadrant can be calculated according to (54) as

$$ \frac{\partial \textbf{Q}^{1,1}}{\partial\theta_{m}} = -\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2} R_{i,j}. $$
(56)

and, through the derivation shown in Appendix Appendix, to the following expression for the upper right quadrant

$$ \frac{\partial Q^{1,2}_{i,j k}}{\partial \theta_{m}} = \left\{\begin{array}{llll} \left[\frac{1}{\theta_{m}}-\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2}\right]Q^{2,1}_{i,j k} &,m=k\\ -\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2} Q^{1,2}_{i,j k} &,m \neq k\end{array}\right., $$
(57)

and the lower right quadrant

$$ \begin{array}{llll} &\frac{\partial Q^{2,2}_{i l,j k}}{\partial \theta_{m}} = &\left\{\begin{array}{lllll} -\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2} Q^{2,2}_{i l,j k} &, m \neq k, m \neq l\\ \left[\frac{1}{\theta_{k}}-\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2}\right]Q^{2,2}_{i l,j k} &, m = k, m \neq l\\ \left[\frac{1}{\theta_{l}}-\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2}\right]Q^{2,2}_{i l,j k} &, m \neq k, m = l\\ \left[2-8\theta_{k}\left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2}\right]R_{i,j} - \left( {x^{m}_{i}}-{x^{m}_{j}}\right)^{2} Q^{2,2}_{i l,j k} &, m = k, m = l\end{array} \right. \end{array}, $$
(58)

for i = 1,...,p, j = 1,...,p, k = 1,...,n and l = 1,...,n.

7 Computational performance

In order to get an idea of the computational cost of obtaining the function values and the partial derivatives of the parameter tuning problem a benchmark example was carried out. The benchmark was carried out using a 76 design variable analytical function with 100 training points. The computational cost of the various routines for the gradient enhanced case are outlined in Table 1. It is shown that the cost of calculating the condensed log likelihood function value and the condition number of the correlation matrix adds up to 6.9 seconds while their partial derivatives with respect to the hyper parameters and regularisation parameters takes 45.3 seconds. This means that for this particular case the cost of the partial derivatives are 6.6 times more expensive than the function values themselves. This is of course less costly than obtaining the gradients through the direct method or finite differences which would incurr a computational cost of around 76 times (the number of design variables) the cost of performing a function evaluation.

Table 1 Computational cost for evaluation of the various variables in kriging for a test problem with 76 design variables and 100 training points
Full size table

8 Proposed optimisation approach

In the proposed approach the aim is to use the derived gradients for hyper parameter optimisation using gradient based methods. Here a method for choosing bounds and a suitable start-point for a gradient based optimisation algorithm is presented.

8.1 Finding a suitable starting point

As seen in, for instance, (Chung and Alonso 2002) it is possible to reduce the complexity of the hyper-parameter optimisation problem by considering the set of hyper-parameters as a single variable according to

$$ \theta = \left[ \theta_{1}, ..., \theta_{n} \right] = \gamma \left[ 1, ..., 1 \right] $$
(59)

where γ is the single considered variable. This is more commonly known as a radial basis function (RBF). The resulting, reduced, optimisation problem can be solved using a one dimensional line search, in this case a golden search (GS). This greatly reduces the computational cost of the optimisation problem but also limits the optimisation to find a solution on the hyper diagonal of the design space. Here, instead of accepting the resulting point as the final solution, it is used as a starting point for optimisation in full space. The reduced optimisation problem is defined as

$$ \begin{array}{lllll} & \underset{\gamma}{\text{maximise}} & & \phi(\theta) \\ & \text{subject to} & & \kappa(\textbf{R}(\theta)) \leq \kappa_{max} \\ & & & {\theta} = \gamma\left[ 1, ..., 1 \right] \\ & & & 0 < \gamma \leq \gamma_{max} \\ \end{array} $$
(60)

where κ m a x is the upper bound constraint on the condition number, chosen as a user input, and γ m a x is the upper bound of the single hyper parameter, chosen such that all off diagonal elements of the correlation matrix can become sufficiently small, i.e. such that m i n(R i j ) = R m i n ,i ≠ j, where R m i n is a user input. In this work R m i n = 10−6.

8.2 Gradient based optimisation

After a starting point has been found through the golden search a gradient based method is to be used in order to explore the full hyper-parameter and regularisation parameter space. Two gradient based optimisation methods are considered, the method of feasible directions (MFD) developed by Vanderplaats (1973) based on the work of Zoutendijk (1960) and sequential quadratic programming (SQP) developed by Madsen et al. (2002) based on the work of Powell (1978).

To ensure a well conditioned correlation matrix at the solution, the condition number is constrained throughout the optimisation. This is enabled through use of the gradients of the condition number with respect to the hyper and regularisation parameters as outlined in Section 6.

9 Comparative study of optimisation approaches

In this section the proposed approach outlined in the previous section is compared to a selection of optimisation approaches, listed in Table 2. These approaches include sequential quadratic programming (SQP) and method of feasible directions (MFD) from one random (R-) start point , 10 multi (M-) start-points and the proposed method whereby the start-point is found by a golden search (GS-). Furthermore a genetic algorithm (GA) with 5000 evaluations and MDF and SQP starting from the resulting GA solution is included in the study.

Table 2 Considered optimisation methods and corresponding abbreviations
Full size table

The study consists of two parts. The first one is carried out on two dimensional functions and the second on a dimensionally scalable problem.

9.1 Two dimensional benchmark study

This study investigates and compares the performance of the optimisation approaches on a suite of two dimensional analytical functions. The functions used in the case study, selected from those presented in Jamil and Yang (2013), are presented in Table 3. In order to reduce the risk of sporadic solutions 50 design of experiments (DOEs) were generated using different seed. Each of these were used in the optimisation of the tuning parameters for the metamodel.The mean time spent, the mean resulting condensed log likelihood and the mean generalisation error of the metamodels, for each of the optimisation approaches, is shown in Table 4.

Table 3 Two dimensional benchmark functions
Full size table
Table 4 Condensed log-likelihood of gradient enhanced kriging metamodel built using 12 training points averaged over 50 training DoEs
Full size table

The GA, GA-MFD and GA-SQP provide the highest condensed log-likelihood values, however these methods take the longest of the tested methods as the number of evaluations carried out by GA within the 2D design variable space is exhaustive. The GS, R-MFD and R-SQP provide the worst results. It is possible to increase the likelihood that a good value is found by the MFD and SQP by using a multi-start strategy as shown, however this increases the amount of time required to build the metamodel. The GS-MFD and GS-SQP provide similar resulting values of the condensed log-likelihood function to the GA-MFD and GA-SQP results at a far lower computation cost. In this case the M-MFD is also finding high values of the condensed log likelihood function to a relatively low computational cost, albeit higher than the GS-MFD and GS-SQP. It is worth noting that for these functions there seems to be a good correlation between a high log likelihood and a low generalisation error.

9.2 Dimensionally scalable benchmark study

This study aims to benchmark the optimisation techniques for functions with higher dimensionality. This was done using the following dimensionally scalable polynomial function

$$ \begin{array}{lllll} &f(\textbf{x}) =\frac{i}{n} \underset{{i}}{\sum} c_{1}{x^{3}_{i}} + c_{2}{x^{2}_{i}} + c_{3}x_{i} + c_{4} + c_{5} sin(fx_{i})\\ &c_{1} = 0.5 \\ &c_{2} = -2.02\left( i-\frac{n}{2}\right) \\ &c_{3} = 7.0\left( i-\frac{n}{2}\right) \\ &c_{4} = 1.0 \\ &c_{5} = 35.0 \\ &c_{6} = 1.0 \\ \end{array} $$
(61)

where n is the total number of design variables, chosen as 10, 40 and 60 respectively in this benchmark study. The function has varying degrees of non-linearity between the different design variables and is evaluated in the range 0 to 5. As with the 2D function 50 different training DOEs were evaluated for each of the three cases in order to reduce the risk of sporadic solutions.

Tables 5, 6 and 7 show the results of the parameter tuning for the dimensionally scalable polynomial in the cases of 10, 40 and 60 design variables respectively. For the 10 design variable case, Table 5, it can be seen that the GS-MFD and GS-SQP perform very well in comparison to the other algorithms, providing the highest log-likelihood together with the hybrid GAs. In this case the remaining algorithms do not perform as well.The GS-MFD and GS-SQP provide the lowest generalised error over the 50 validation DoEs, followed by the GA-MFD and GA-SQP.

Table 5 Scalable polynomial 10 design variables
Full size table
Table 6 Scalable polynomial 40 design variables
Full size table
Table 7 Scalable polynomial 60 design variables
Full size table

When increasing dimensionality of the scalable polynomial function to 40 design variables the benefit of the proposed approach becomes more apparent. The proposed approach delivers a solution with high mean condensed log-likelihood value for a low computational effort when compared to the other evaluated methods. The GS-SQP provides the highest mean condensed log-likelihood value for all numbers of training points. The GS-MFD provides the second highest mean log likelihood over all of the number of training points, followed by the GA-SQP. In the 50 training point case the M-SQP provides the second highest mean condensed log likelihood. However for the 10 and 20 training point cases does not perform as well. For the 10 and 20 training point cases the GS-MFD and GS-SQP take slightly longer to build than the R-MFD and R-SQP. However for the 50 training point case the GS-SQP takes less than half the time taken to build the R-SQP. The lowest generalisation error is provided by the GS, GS-MFD and GS-SQP. As more training points are used the GS-MFD and GS-SQP provide a better generalisation error.

In the final case with 60 design variables the GS-MFD and GS-SQP also perform very well. For 10 and 20 training points they provide the highest mean log-likelihood values. For 50 training points the GS-SQP provides the highest mean condensed log likelihood followed closely by the M-SQP, then the GA-SQP and R-SQP, at 25, 15 and 2.5 times the computational effort respectively.

Of the proposed methods the GS-MFD and GS-SQP provide the best results for the time required to build the metamodels. They consistently outperform the random start point, GA-MFD and GA-SQP methods. As the dimensionality of the scalable polynomial function increases the benefit of using the solution of the GS as a starting point for the MFD or SQP increases. Overall the GS-SQP provides the best mean log-likelihood for the time required to build the metamodel, as such will be used in Section 10 for a industrial sized test case.

10 Case study: aircraft wing example

This section presents a study where gradient enhanced kriging metamodels are created for a finite element model of an aircraft wing. The GS-MFD and GS-SQP methods are compared to the GS, R-MFD and R-SQP methods. The multi-start and GA start point methods are not included as the computational effort would be too great.

10.1 The wing model

The wing model consists of 126 aluminium sheet panels with designable thickness; as shown in Fig. 4. Each of the design variables are aluminium sheets which are modelled with shell elements with a mesh size of 18mm. The allowable thickness range is from 0.5 mm–5 mm with a nominal thickness of 2.5 mm.

Fig. 4
figure 4

Wing panel design variables

Full size image

The wing is fully constrained on the wider end to represent attachment to the fuselage. Forces and moments are applied to nodes located at the centroid of each rib, as shown in Fig. 5a and b, and distributed to the edges of the rib using one dimensional distributing coupling (RBE3) elements. An example of the deformation due to the loading is shown in Fig. 5c. Two responses are considered: vertical wing tip deflection and the rotation of the wing tip. Deflection and rotation are measured in horizontal centre and vertical top of the wing tip.

Fig. 5
figure 5

Wing loading

Full size image

The model is analysed using OptiStruct v13.0.210 (Altair Engineering Inc 2014). OptiStruct provides analytical gradients via either the direct or the adjoint method depending on which is the more efficient choice for the case. In this case the adjoint method is used as the number of design variables is far greater than the number of responses; evaluating the gradients took roughly the same time as evaluating the function values, doubling the total analysis time.

10.2 Study set-up

The study was performed by building the meta-models with 5 points at first, followed by 10, 20, 50 points. For this purpose, sampling was performed using MELS. One benefit of MELS is that any subset of the DoE in sequence from the first point is suitably spaced. This allows the user to assess the approximation quality interactively allowing for a far more flexible approach than would be possible with other space filling techniques such as the Optimal Latin Hypercube (Audze and Eglajs 1977). To leverage this feature a single DoE of was created. 50 points were reserved for training the metamodels and 500 points were reserved for validation.

10.3 Results

Tables 8 and 9 show the performance of the GS-MFD and GS-SQP is compared with that of the GS, R-MFD and R-SQP. In Table 8a the condensed log likelihood obtained by the different optimisation methods is shown for the wing tip displacement, it can be seen that the GS-SQP outperforms the other methods, closely followed by the GS-MFD which are second best in all cases apart from in the 10 point case where R-SQP provides a slightly better solution.

Table 8 Results for wing tip displacement
Full size table
Table 9 Results for wing tip rotation
Full size table

In Table 8b the generalisation error obtained for the different optimisation methods is shown. It can be seen that GS, GS-MFD and GS-SQP provide solutions which outperform R-MFD and R-SQP. It can also be seen that even though GS-MFD and GS-SQP provide condensed log likelihood values which are higher than the one for GS, the generalisation error is not necessarily improved.

Table 9a shows that, for wing tip rotation, the GS-MFD and GS-SQP out perform the other evaluated methods, which is reflected in the generalisation error, Table 9b. Similarly to the wing tip displacement, the golden search optimisation method shows lower resulting generalisation error than the R-MFD and R-SQP.

11 Conclusions

In this work an approach was suggested for efficient hyper parameter optimisation for building well conditioned gradient enhanced kriging metamodels. The approach consists of two steps, a one dimensional line search where all hyper-parameters are treated as one variable, and a gradient based optimisation starting from the solution of the initial line search. In order to ensure a suitable condition number of the correlation matrix, an upper bound constraint was enforced. Partial derivatives of the condition number with respect to the correlation matrix was derived in order to use this constraint in the gradient based optimisation approach. Both the method of feasible directions and sequential quadratic programming was evaluated within the approach.

The approach was compared to random start point gradient based algorithms, multiple start point gradient based algorithms and a genetic algorithm followed by gradient based algorithms from promising points. It was shown that the approach outperforms random start-point and multi-start gradient based algorithms in terms of both computational performance and quality of solutions. The comparative study shows the SQP to be the better choice of algorithm within the approach as it provides slightly higher condensed log-likelihood values than the MFD for a similar time to build.

The proposed approach, using both the SQP and MFD, was compared to a selection of the other optimisation approaches using an aircraft wing model comprising of 126 thickness design variables. The GS-SQP consistently provides the highest condensed log likelihood value closely followed by the GS-MFD.

In some case it was shown that a big improvement in log likelihood did not necessarily translate to an improvement in generalisation error. This was particularly apparent for the wing tip displacement metamodels where the GS-SQP provided a higher condensed log likelihood than the GS case but the generalisation error was of comparable magnitude.

A possible limitation of the proposed strategy may be the assumption made when finding the starting point, that the optimum lies close to the hyper diagonal of the hyper parameter space. If this assumption is not correct for a given problem then the efficiency of the proposed strategy may be reduced. However this was not shown in the scalable polynomial example which was chosen for it’s varying non-linearity between design variables.