Skip to main content
SpringerLink
Log in

On the (non-)optimality of Michell structures

  • RESEARCH PAPER
  • Published:
Structural and Multidisciplinary Optimization Aims and scope Submit manuscript

Abstract

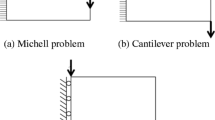
Optimal analytical Michell frame structures have been extensively used as benchmark examples in topology optimization, including truss, frame, homogenization, density and level-set based approaches. However, as we will point out, partly the interpretation of Michell’s structural continua as discrete frame structures is not accurate and partly, it turns out that limiting structural topology to frame-like structures is a rather severe design restriction and results in structures that are quite far from being stiffness optimal. The paper discusses the interpretation of Michell’s theory in the context of numerical topology optimization and compares various topology optimization results obtained with the frame restriction to cases with no design restrictions. For all examples considered, the true stiffness optimal structures are composed of sheets (2D) or closed-walled shell structures (3D) with variable thickness. For optimization problems with one load case, numerical results in two and three dimensions indicate that stiffness can be increased by up to 80 % when dropping the frame restriction. For simple loading situations, studies based on optimal microstructures reveal theoretical gains of +200 %. It is also demonstrated how too coarse design discretizations in 3D can result in unintended restrictions on the design freedom and achievable compliance.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

Notes

  1. 1 We note that the term “optimal”is grossly overused in the discussion of numerical topology optimization results in the literature, however, the variable thickness sheet problem is indeed a convex problem and hence convergence to global optima can in this case be guaranteed.

  2. 2 Note that the analytical Michell solution is pin-supported at the lower corners but this would cause stress singularities when modeled using a continuum formulation. We have found that reducing the line support to the lower three rightmost and leftmost elements, mimicking a pinned support does not change the conclusions of this study.

References

  • Aage N., Andreassen E., Lazarov B. (2015) Topology optimization using PETSc: An easy-to-use, fully parallel, open source topology optimization framework. Struct Multidiscip Optim 51(3):565– 572

    Article  MathSciNet  Google Scholar 

  • Allaire G., Kohn R.V. (1993) Explicit bounds on the elastic energy of a two-phase composite in two space dimensions. Q Appl Math 51:675–699

    MathSciNet  MATH  Google Scholar 

  • Amir O., Aage N., Lazarov B. (2014) On multigrid-cg for efficient topology optimization. Struct Multidiscip Optim 49(5):815–829

    Article  MathSciNet  Google Scholar 

  • Andreassen E., Andreasen C. (2014) How to determine composite material properties using numerical homogenization. Comput Mater Sci 83:488–495. doi:10.1016/j.commatsci.2013.09.006

    Article  Google Scholar 

  • Balay S., Abhyankar S., Adams M., Brown J., Brune P., Buschelman K., Dalcin L., Eijkhout V., Gropp W., Kaushik D., Knepley M., McInnes L., Rupp K., Smith B., Zampini S., Zhang H. (2015) PETSc users manual. Tech. Rep. ANL-95/11 - Revision 3.6, Argonne National Laboratory. http://www.mcs.anl.gov/petsc

  • Beghini L., Beghini A., Katz N., Baker W., Paulino G. (2014) Connecting architecture and engineering through structural topology optimization. Eng Struct 59:716–726. doi:10.1016/j.engstruct.2013.10.032

    Article  Google Scholar 

  • Bendsøe M.P. (1989) Optimal shape design as a material distribution problem. Structural Optimization 1:193–202

    Article  Google Scholar 

  • Bendsøe M.P., Haber R.B. (1993) The Michell layout problem as a low volume fraction limit of the perforated plate optimization problem: An asymptotic study. Struct Optim 6:263–267

    Article  Google Scholar 

  • Bendsøe M.P., Kikuchi N. (1988) Generating optimal topologies in structural design using a homogenization method. Comput Methods Appl Mech Eng 71(2):197–224

    Article  MathSciNet  MATH  Google Scholar 

  • Bendsøe M.P., Sigmund O. (1998) Optimering af konstruktioners topologi, form og materiale. Udstillingen

  • Bendsøe M.P., Sigmund O. (2004) Topology Optimization - Theory Methods and Applications. Springer Verlag, Heidelberg

    MATH  Google Scholar 

  • Chan A. (1960) The design of Michell optimum structures. Cranfield College of Aeronautics

  • Francfort G.A., Murat F. (1986) Homogenization and optimal bounds in linear elasticity. Arch Ration Mech Anal 94(4):307–334

    Article  MathSciNet  MATH  Google Scholar 

  • Gibiansky L.V., Sigmund O. (2000) Multiphase elastic composites with extremal bulk modulus. J Mech Phys Solids 48(3):461–498

    Article  MathSciNet  MATH  Google Scholar 

  • Grabovsky Y., Kohn R.V. (1995) Anisotropy of the Vigdergauz microstructure. J Appl Mech 62(4):1063–1065

    Article  MATH  Google Scholar 

  • Graczykowski C., Lewiński T. (2010) Michell cantilevers constructed within a half strip. tabulation of selected benchmark results. Struct Multidiscip Optim 42(6):869–877

    Article  Google Scholar 

  • Guedes J.M., Kikuchi N. (1990) Preprocessing and postprocessing for materials based on the homogenization method with adaptive finite element methods. Comput Methods Appl Mech Eng 83:143–198

    Article  MathSciNet  MATH  Google Scholar 

  • Guest J., Prevost J., Belytschko T. (2004) Achieving minimum length scale in topology optimization using nodal design variables and projection functions. Int J Numer Methods Eng 61(2):238–254

    Article  MathSciNet  MATH  Google Scholar 

  • Hashin Z. (1962) The elastic moduli of heterogeneous materials. ASME J Appl Mech 29:143–150

    Article  MathSciNet  MATH  Google Scholar 

  • Hassani B., Hinton E. (1998) A review of homogenization and topology optimization I-homogenization theory for media with periodic structure. Compos Struct 69(6):707–717

    Article  MATH  Google Scholar 

  • Lurie K.A., Cherkaev A.V. (1984) G-closure of a set of anisotropically conducting media in the two-dimensional case. J Optim Theory Appl 42(2):283–304

    Article  MathSciNet  MATH  Google Scholar 

  • Martinez P., Marti P., Querin O. (2007) Growth method for size, topology, and geometry optimization of truss structures. Struct Multidiscip Optim 33(1):13–26. doi:10.1007/s00158-006-0043-9

    Article  Google Scholar 

  • Michell A.G.M. (1904) The limit of economy of material in frame structures. Philos Mag 8(6):589–597

    Article  MATH  Google Scholar 

  • Milton G.W. (1986) Modelling the properties of composites by laminates. In: Ericksen JL, Kinderlehrer D, Kohn R, Lions JL (eds) Homogenization and Effective Moduli of Materials and Media, IMA, vol 1. Springer Verlag, pp 150–174

  • Nguyen T., Paulino G., Song J., Le C. (2012) Improving multiresolution topology optimization via multiple discretizations. Int J Numer Methods Eng 92(6):507–530

    Article  MathSciNet  Google Scholar 

  • Norris A.N. (1985) A differential scheme for the effective moduli of composites. Mech Mater 4:1–16

    Article  Google Scholar 

  • Rossow M.P., Taylor J.E. (1973) A finite element method for the optimal design of variable thickness sheets. AIAA J 11:1566–1569

    Article  Google Scholar 

  • Rozvany G.I.N. (1998) Exact analytical solutions for some popular benchmark problems in topology optimization. Structural Optimization 15(1):42–46

    Article  MATH  Google Scholar 

  • Rozvany G.I.N., Ong T.G., Szeto W.T., Sandler R., Olhoff N., Bendsø MP (1987) Least-weight design of perforated elastic plates. I Int J Solids Struct 23(4):521–36

    Article  MATH  Google Scholar 

  • Sigmund O. (1999) On the optiMality of bone microstructure. In: Pedersen P, Bendsø MP (eds) Synthesis in Bio Solid Mechanics, IUTAM. Kluwer, pp 221–234

  • Sigmund O. (2000) A new class of extremal composites. J Mech Phys Solids 48(2):397–428

    Article  MathSciNet  MATH  Google Scholar 

  • Sigmund O. (2001) A 99 line topology optimization code written in MATLAB. Struct Multidiscip Optim 21:120–127. doi:10.1007/s001580050176. MATLAB code available online at: www.topopt.dtu.dk

    Article  Google Scholar 

  • Sigmund O. (2007) Morphology-based black and white filters for topology optimization. Struct Multidiscip Optim 33(4-5):401–424

    Article  Google Scholar 

  • Sundström B. (2010) Handbook of solid mechanics. Department of Solid Mechanics, KTH

  • Vigdergauz S.B. (1989) Regular structures with extremal elastic properties. Mechanics of Solids 24:57–63

    Google Scholar 

  • Vigdergauz S.B. (1994) Three-dimensional grained composites of extreme thermal properties. J Mech Phys Solids 42(5):729–740

    Article  MathSciNet  MATH  Google Scholar 

  • Vigdergauz S.B. (1999) Energy-minimizing inclusions in a planar elastic structure with macroisotropy. Structural Optimization 17(2-3):104–112

    Article  Google Scholar 

  • Villanueva C., Maute K. (2014) Density and level set-xfem schemes for topology optimization of 3-d structures. Comput Mech 54(1):133–150. doi:10.1007/s00466-014-1027-z

    Article  MathSciNet  MATH  Google Scholar 

  • Wang F., Lazarov B., Sigmund O. (2011) On projection methods, convergence and robust formulations in topology optimization. Struct Multidiscip Optim 43(6):767–784. doi:10.1007/s00158-010-0602-y

    Article  MATH  Google Scholar 

  • Xu S., Cai Y., Cheng G. (2010) Volume preserving nonlinear density filter based on heaviside funtions. Struct Multidiscip Optim 41:495–505

    Article  MathSciNet  MATH  Google Scholar 

  • Zhou M., Rozvany G.I.N. (1991) The COC algorithm, part II: Topological, geometry and generalized shape optimization. Comput Methods Appl Mech Eng 89(1-3):309–336

    Article  Google Scholar 

Download references

Acknowledgments

The authors dedicate this paper to George Rozvany (1930-2015): partly due to his life-long and great efforts in providing and promoting benchmarks to the structural optimization society; partly for valuable email exchanges concerning the benchmark examples used in this paper; and partly for his general and significant scientific and personal impact on the field of structural and multidisciplinary optimization and on the first author’s scientific career in particular.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, Solid Mechanics, Technical University of Denmark, 2800 Kgs., Lyngby, Denmark

    Ole Sigmund, Niels Aage & Erik Andreassen

Authors
  1. Ole Sigmund
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Niels Aage
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erik Andreassen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ole Sigmund.

Additional information

This paper is dedicated to George Rozvany (1930-2015) - see more in the acknowledgement

This work was funded by the Villum Foundation through the NextTop project.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sigmund, O., Aage, N. & Andreassen, E. On the (non-)optimality of Michell structures. Struct Multidisc Optim 54, 361–373 (2016). https://doi.org/10.1007/s00158-016-1420-7

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00158-016-1420-7

Keywords

Search

Navigation