An affine generalization of evacuation

Abstract

We establish the existence of an involution on tabloids that is analogous to Schützenberger’s evacuation map on standard Young tableaux. We find that the number of its fixed points is given by evaluating a certain Green’s polynomial at $q = -1$, and satisfies a “domino-like” recurrence relation.

Appendix A: More on rigged configurations

In this appendix, we describe the forward direction of the bijection $\Phi : \mathrm{SSYT}(\lambda ,\mu ) \rightarrow \mathrm{RC}(\lambda ,\mu )$ for the reader’s convenience, and we explain how Theorem 4.11 follows from results of Kirillov, Schilling, and Shimozono [20].

1.1 A.1. The rigged configuration bijection

Recall that a rigged configuration is a pair $(\nu , J)$, where $\nu = (\nu ^{(1)}, \nu ^{(2)}, \ldots )$ is sequence of partitions, and J is an assignment of a non-negative integer rigging to each row of each partition, such that the rigging attached to a row of length r in $\nu ^{(k)}$ is at most the vacancy number $P_r^{(k)}(\nu )$. Say that a row of the partition $\nu ^{(k)}$ is a singular string if its rigging is equal to the corresponding vacancy number; by convention, every partition has a singular string of length 0.

Definition–Proposition A.1

(Kirillov–Reshetikhin [18]) The bijection $\Phi : \mathrm{SSYT}(\lambda ,\mu ) \rightarrow \mathrm{RC}(\lambda ,\mu )$ of Theorem 4.11 is computed recursively as follows. The empty tableau maps to the empty rigged configuration. Given a non-empty tableau T, let d be the maximum entry of T, and let U be the tableau obtained from T by removing the right-most box in T that contains d. Assume that $\Phi (U) = (\nu , J)$ has been computed; we explain how to construct $\Phi (T) = (\nu ', J')$. Suppose the box removed from T is in row r. Set $m_r = \infty$ and define a sequence

$$\begin{aligned} m_{r-1} \ge m_{r-2} \ge \cdots \ge m_1 \ge 0 \end{aligned}$$

by taking $m_j$ to be the biggest number less than or equal to $m_{j+1}$ such that $\nu ^{(j)}$ contains a singular string of length $m_j$. The configuration $\nu '$ is obtained from $(\nu , J)$ by adding one box to a singular string of length $m_j$ in $\nu ^{(j)}$ for each $j \le r-1$. For each of these $r-1$ changed rows, the rigging is chosen so that the row is a singular string with respect to the vacancy numbers of $\nu '$. The riggings of all other rows are unchanged.

An algorithm for the other direction is given in [18,  § 3].

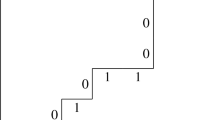
Example A.2

Figure 3 shows one step of the algorithm for $\Phi$. To obtain the rigged configuration in Example 4.10 corresponding to the tableau in Example 4.12, one performs two more steps of the algorithm. The first of these steps adds a box to the fourth row of $\mu$, which causes the vacancy numbers of $\nu ^{(1)}$ to increase from 1 to 2.

Fig. 3

One step in the algorithm for $\Phi$. The number to the left of a row is its rigging, and the number to the right its vacancy number

In Sect. 4.3.2, we required that $\mu$ be a partition. In fact, for any strict composition $\mu = \langle \mu _1, \ldots , \mu _d \rangle$, the algorithm in Definition-Proposition A.1 gives a bijection $\Phi _\mu : \mathrm{{SSYT}}(\lambda , \mu ) \rightarrow \mathrm{{RC}}(\lambda , \mathrm{{sort}}(\mu ))$, where $\mathrm{{sort}}(\mu )$ is the partition obtained by sorting the parts of $\mu$.⁷ The existence of these bijections implies that for a permutation $w \in \mathfrak {S}_d$, the composition $\Phi _{w \mu }^{-1} \circ \Phi _\mu$ defines a shape-preserving, content-permuting action of the symmetric group on semistandard tableaux. It is asserted in [20] that this action agrees with the action introduced in Sect. 3.4; we supply the omitted proof.

Lemma A.3

For $T \in \mathrm{{SSYT}}(\lambda ,\mu )$ and $w \in \mathfrak {S}_d$,

$$\begin{aligned} \Phi _{w \mu }^{-1} (\Phi _\mu (T)) = w(T), \end{aligned}$$

where w(T) denotes the action of Definition–Proposition 3.22.

Proof

It suffices to consider the generators $s_i$. By [20,  Def.-Prop. 8.1 and Lem. 8.5], the maps $\Psi _i := \Phi _{s_i \mu }^{-1} \circ \Phi _\mu$ are characterized by the properties that $\Psi _i$ does not change entries greater than $i+1$, and $\Psi _{d-1} \circ e_d = e_d \circ \Psi _1$, where $e_d$ is the evacuation map on semistandard tableaux with entries at most d. The maps $s_i$ of Definition-Proposition 3.22 satisfy the first property by definition, and the second property by, e.g., [39,  Prop. 2.87(iii)]. $\square$

1.2 A.2. Relation with work of Kirillov–Schilling–Shimozono

The rigged configurations discussed in Sect. 4.3.2 are a special case of a more general theory of rigged configurations developed by Kirillov, Schilling, and Shimozono in [20]. In this section we introduce the more general setup and notation of that paper, state several of their main theorems, and explain how these theorems imply Theorem 4.11.

Let $\mathcal {R} = (\mathcal {R}_1, \ldots , \mathcal {R}_d)$ be a sequence of rectangular partitions, and $\lambda$ an arbitrary partition. In [20], the authors define a set $\mathrm{{CLR}}(\lambda ; \mathcal {R})$ of Littlewood–Richardson tableaux. The elements of $\mathrm{{CLR}}(\lambda ; \mathcal {R})$ are a subset of the standard tableaux of shape $\lambda$, and the cardinality of $\mathrm{{CLR}}(\lambda ; \mathcal {R})$ is equal to the multiplicity of the Schur function $s_{\lambda }$ in the product $s_{\mathcal {R}_1} \cdots s_{\mathcal {R}_d}$. In particular, when $\mathcal {R} = \mathcal {R}(\mu ) := (\langle \mu _1 \rangle , \ldots , \langle \mu _d \rangle )$ is a sequence of one-row partitions, the cardinality of $\mathrm{{CLR}}(\lambda ; \mathcal {R}(\mu ))$ is the Kostka number $K_{\lambda \mu }$, and $\mathrm{{CLR}}(\lambda ; \mathcal {R}(\mu ))$ consists of the standardizations⁸ of the elements of $\mathrm{{SSYT}}(\lambda , \mu )$. Let ${\text {std}}$ denote the standardization map $\mathrm{{SSYT}}(\lambda , \mu ) \rightarrow \mathrm{{CLR}}(\lambda ; \mathcal {R}(\mu ))$.

We recall several properties of Littlewood–Richardson tableaux. First, evacuation of standard tableaux restricts to a bijection $e: \mathrm{{CLR}}(\lambda ; \mathcal {R}) \rightarrow \mathrm{{CLR}}(\lambda ; w_0(\mathcal {R}))$, where $w_0(\mathcal {R}) = (\mathcal {R}_d, \ldots , \mathcal {R}_1)$ [20,  paragraph after Lem. 3.8]. Let $\eta ^t$ denote the transpose (or conjugate) of the partition $\eta$, and let $\mathcal {R}^t = (\mathcal {R}_1^t, \ldots , \mathcal {R}_d^t)$. There is a bijection $\mathrm{{tr_{LR}}}: \mathrm{{CLR}}(\lambda ; \mathcal {R}) \rightarrow \mathrm{{CLR}}(\lambda ^t; \mathcal {R}^t)$ [20,  Def. 2.7], and a generalized charge statistic $c_\mathcal {R} : \mathrm{{CLR}}(\lambda ; \mathcal {R}) \rightarrow \mathbb {Z}_{\ge 0}$ defined in [33, 37]. By [38,  Prop. 26 and Thm. 28] or [33,  Lem. 6.5], one has

$$\begin{aligned} c_{\mathcal {R}^t}(\mathrm{{tr_{LR}}}(T)) = n(\mathcal {R}) - c_\mathcal {R}(T) \end{aligned}$$

(A.1)

for $T \in \mathrm{{CLR}}(\lambda ; \mathcal {R})$, where $n(\mathcal {R}) = \sum _{i < j} |\mathcal {R}_i \cap \mathcal {R}_j|$ and $\mathcal {R}_1 \cap \mathcal {R}_2$ denotes intersection of Young diagrams. When $\mathcal {R} = \mathcal {R}(\mu )$, $\mathrm{{tr_{LR}}}$ is simply the reflection of a standard tableau over the main diagonal, and

$$\begin{aligned} c_{\mathcal {R}(\mu )}(T) = c({\text {std}}^{-1}(T)), \end{aligned}$$

(A.2)

where c is the usual charge statistic on semistandard tableaux.⁹ Note also that $n(\mathcal {R}(\mu )) = b(\mathrm{{sort}}(\mu )) = \sum (i-1)(\mathrm{{sort}}(\mu ))_i$.

Kirillov, Schilling, and Shimozono also define a notion of rigged configuration of type $(\lambda ; \mathcal {R})$; they denote the set of these by $\mathrm{{RC}}(\lambda ; \mathcal {R})$. A rigged configuration of type $(\lambda ; \mathcal {R}(\mu ))$ is the same as a rigged configuration of type $(\lambda , \mathrm{{sort}}(\mu ))$, as defined in Sect. 4.3.2. The involution $\Theta$ and the statistic cc naturally generalize to rigged configurations of type $(\lambda ; \mathcal {R})$. In [20,  §4.1], the authors define a bijection

$$\begin{aligned} \overline{\phi }_\mathcal {R} : \mathrm{{CLR}}(\lambda ; \mathcal {R}) \rightarrow \mathrm{{RC}}(\lambda ^t; \mathcal {R}^t). \end{aligned}$$

Comparing the algorithm of Definition–Proposition A.1 with the description of $\overline{\phi }_\mathcal {R}$ in [20,  §4.2], one sees that

$$\begin{aligned} \Phi _\mu = \overline{\phi }_{\mathcal {R}(\mu )^t} \circ \mathrm{{tr_{LR}}}\circ {\text {std}}. \end{aligned}$$

The definition of a rigged configuration of type $(\lambda ; \mathcal {R})$ does not depend on the ordering of the rectangles in $\mathcal {R}$, so we identify the sets $\mathrm{{RC}}(\lambda ; \mathcal {R})$ and $\mathrm{{RC}}(\lambda ; w_0(\mathcal {R}))$. Also set $\widetilde{\phi }_\mathcal {R} = \Theta \circ \overline{\phi }_\mathcal {R}$.

Theorem A.4

([20,  Thm. 5.6, 9.1]) For $T \in \mathrm{{CLR}}(\lambda ; \mathcal {R})$, one has

• (1) $\Theta (\overline{\phi }_\mathcal {R}(T)) = \overline{\phi }_{w_0(\mathcal {R})}(e(T))$ and

• (2) $cc (\widetilde{\phi }_\mathcal {R}(T)) = c_\mathcal {R}(T)$.

Proof of Theorem 4.11

Suppose $T \in \mathrm{{SSYT}}(\lambda ,\mu )$. Recall that $e^* = w_0 \circ e$. By Lemma A.3,

$$\begin{aligned} \Phi _\mu (e^*(T)) = \Phi _{w_0(\mu )}(e(T)). \end{aligned}$$

By Theorem A.4(1) and the fact that evacuation commutes with both standardization and transposition of standard tableaux, we have

$$\begin{aligned} \Phi _{w_0(\mu )}(e(T)) = \overline{\phi }_{w_0(\mathcal {R}(\mu )^t)} \circ \mathrm{{tr_{LR}}}\circ {\text {std}}(e(T)) = \Theta (\Phi _{\mu }(T)). \end{aligned}$$

Thus, $\Phi _\mu (e^*(T)) = \Theta (\Phi _\mu (T))$, proving part (1).

For part (2), use Theorem A.4(2) and (A.1), (A.2) to obtain

$$\begin{aligned} cc \circ \Theta \circ \Phi _\mu (T) = cc \circ \widetilde{\phi }_{\mathcal {R}(\mu )^t} \circ \mathrm{{tr_{LR}}}\circ {\text {std}}(T) = b(\mu ) - c(T). \end{aligned}$$

$\square$