Asymptotics of Muttalib–Borodin determinants with Fisher–Hartwig singularities

Abstract

Muttalib–Borodin determinants are generalizations of Hankel determinants and depend on a parameter $\theta >0$. In this paper, we obtain large n asymptotics for $n \times n$ Muttalib–Borodin determinants whose weight possesses an arbitrary number of Fisher–Hartwig singularities. As a corollary, we obtain asymptotics for the expectation and variance of the real and imaginary parts of the logarithm of the underlying characteristic polynomial, several central limit theorems, and some global bulk rigidity upper bounds. Our results are valid for all $\theta > 0$.

Model RH problems

In this section, $\alpha$ and $\beta$ are such that $\text {Re}\,\alpha >-1$ and $\text {Re}\,\beta \in (-\frac{1}{2},\frac{1}{2})$.

1.1 Bessel model RH problem for $\Phi _{\mathrm {Be}}(\cdot ) = \Phi _{\mathrm {Be}}(\cdot ;\alpha )$

• (a) $\Phi _{\mathrm {Be}} : {\mathbb {C}} \setminus \Sigma _{\mathrm {Be}} \rightarrow {\mathbb {C}}^{2\times 2}$ is analytic, where $\Sigma _{\mathrm {Be}} = (-\infty ,0]\cup e^{\frac{2\pi i}{3}}(0,+\infty ) \cup e^{-\frac{2\pi i}{3}}(0,+\infty )$ and is oriented as shown in Fig. 6.

• (b) $\Phi _{\mathrm {Be}}$ satisfies the jump relations

  $$\begin{aligned} \begin{array}{l l} \Phi _{\mathrm {Be},+}(z) = \Phi _{\mathrm {Be},-}(z) \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix}, &{} z \in (-\infty ,0), \\ \Phi _{\mathrm {Be},+}(z) = \Phi _{\mathrm {Be},-}(z) \begin{pmatrix} 1 &{} 0 \\ e^{\pi i \alpha } &{} 1 \end{pmatrix}, &{} z \in e^{ \frac{2\pi i}{3} } (0,+\infty ), \\ \Phi _{\mathrm {Be},+}(z) = \Phi _{\mathrm {Be},-}(z) \begin{pmatrix} 1 &{} 0 \\ e^{-\pi i \alpha } &{} 1 \end{pmatrix}, &{} z \in e^{ -\frac{2\pi i}{3} } (0,+\infty ). \\ \end{array} \end{aligned}$$

  (A.1)

• (c) As $z \rightarrow \infty$, $z \notin \Sigma _{\mathrm {Be}}$,

  $$\begin{aligned} \Phi _{\mathrm {Be}}(z) = ( 2\pi z^{\frac{1}{2}} )^{-\frac{\sigma _{3}}{2}}A \left( I+\sum _{k=1}^{\infty } \Phi _{\mathrm {Be},k} z^{-k/2}\right) e^{2z^{\frac{1}{2}}\sigma _{3}}, \qquad A = \frac{1}{\sqrt{2}}\begin{pmatrix} 1 &{} i \\ i &{} 1 \end{pmatrix},\nonumber \\ \end{aligned}$$

  (A.2)

  where the matrices $\Phi _{\mathrm {Be},k}$ are independent of z, and

  $$\begin{aligned} \Phi _{\mathrm {Be},1} = \frac{1}{16}\begin{pmatrix} -(1+4\alpha ^{2}) &{} -2i \\ -2i &{} 1+4\alpha ^{2} \end{pmatrix}. \end{aligned}$$

  (A.3)

• (d) As $z \rightarrow 0$,

  $$\begin{aligned} \begin{array}{l l} \displaystyle \Phi _{\mathrm {Be}}(z) = \left\{ \begin{array}{l l} \begin{pmatrix} {{\mathcal {O}}}(1) &{} {{\mathcal {O}}}(\log z) \\ {{\mathcal {O}}}(1) &{} {{\mathcal {O}}}(\log z) \end{pmatrix}, &{} |\arg z|< \frac{2\pi }{3}, \\ \begin{pmatrix} {{\mathcal {O}}}(\log z) &{} {{\mathcal {O}}}(\log z) \\ {{\mathcal {O}}}(\log z) &{} {{\mathcal {O}}}(\log z) \end{pmatrix}, &{} \frac{2\pi }{3}< |\arg z|< \pi , \end{array} \right. , &{} \displaystyle \text{ if } \text {Re}\,\alpha = 0, \\ \displaystyle \Phi _{\mathrm {Be}}(z) = \left\{ \begin{array}{l l} \begin{pmatrix} {{\mathcal {O}}}(1) &{} {{\mathcal {O}}}(1) \\ {{\mathcal {O}}}(1) &{} {{\mathcal {O}}}(1) \end{pmatrix}z^{\frac{\alpha }{2}\sigma _{3}}, &{} |\arg z |< \frac{2\pi }{3}, \\ \begin{pmatrix} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) \\ {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) \end{pmatrix}, &{} \frac{2\pi }{3}<|\arg z |< \pi , \end{array} \right. , &{} \displaystyle \text{ if } \text {Re}\,\alpha > 0, \\ \displaystyle \Phi _{\mathrm {Be}}(z) = \begin{pmatrix} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) \\ {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) \end{pmatrix},&\displaystyle \text{ if } \text {Re}\,\alpha < 0. \end{array} \end{aligned}$$

  (A.4)

Fig. 6

The jump contour $\Sigma _{\mathrm {Be}}$ for $\Phi _{\mathrm {Be}}$

The unique solution to this RH problem is expressed in terms of Bessel functions. Since this explicit expression is unimportant for us, we will not write it down. The interested reader can find more information and background on this RH problem in e.g. [53, Section 6].

1.2 Confluent hypergeometric model RH problem

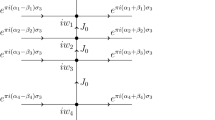
• (a) $\Phi _{\mathrm {HG}} : {\mathbb {C}} \setminus \Sigma _{\mathrm {HG}} \rightarrow {\mathbb {C}}^{2 \times 2}$ is analytic, with $\Sigma _{\mathrm {HG}} = \cup _{j=1}^{8}\Gamma _{j}$, and $\Gamma _{1},\ldots ,\Gamma _{8}$ are shown in Fig. 7.

• (b) $\Phi _{\mathrm {HG}}$ satisfies the jumps

  $$\begin{aligned} \Phi _{\mathrm {HG},+}(z) = \Phi _{\mathrm {HG},-}(z)J_{k}, \qquad z \in \Gamma _{k}, \; k = 1,...,8, \end{aligned}$$

  (A.5)

  where $J_{8} = \begin{pmatrix} 1 &{} 0 \\ e^{i\pi \alpha }e^{i\pi \beta } &{} 1 \end{pmatrix}$ and

  $$\begin{aligned}&\, J_{1} = \begin{pmatrix} 0 &{} e^{-i\pi \beta } \\ -e^{i\pi \beta } &{} 0 \end{pmatrix}, \; J_{5} = \begin{pmatrix} 0 &{} e^{i\pi \beta } \\ -e^{-i\pi \beta } &{} 0 \end{pmatrix},\; J_{3} = J_{7} = \begin{pmatrix} e^{\frac{i\pi \alpha }{2}} &{} 0 \\ 0 &{} e^{-\frac{i\pi \alpha }{2}} \end{pmatrix}, \\&\, J_{2} = \begin{pmatrix} 1 &{} 0 \\ e^{-i\pi \alpha }e^{i\pi \beta } &{} 1 \end{pmatrix}, \; J_{4} = \begin{pmatrix} 1 &{} 0 \\ e^{i\pi \alpha }e^{-i\pi \beta } &{} 1 \end{pmatrix}, \; J_{6} = \begin{pmatrix} 1 &{} 0 \\ e^{-i\pi \alpha }e^{-i\pi \beta } &{} 1 \end{pmatrix}. \end{aligned}$$

  Fig. 7

  

  The jump contour $\Sigma _{\mathrm {HG}}$ for $\Phi _{\mathrm {HG}}$. Each of the rays $\Gamma _{1},\ldots ,\Gamma _{8}$ forms an angle with $(0,+\infty )$ which is a multiple of $\frac{\pi }{4}$

• (c) As $z \rightarrow \infty$, $z \notin \Sigma _{\mathrm {HG}}$, we have

  $$\begin{aligned} \Phi _{\mathrm {HG}}(z) = \left( I + \sum _{k=1}^{\infty } \frac{\Phi _{\mathrm {HG},k}}{z^{k}} \right) z^{-\beta \sigma _{3}}e^{-\frac{z}{2}\sigma _{3}}M^{-1}(z), \end{aligned}$$

  (A.6)

  where

  $$\begin{aligned} \Phi _{\mathrm {HG},1} = \Big (\beta ^{2}-\frac{\alpha ^{2}}{4}\Big ) \begin{pmatrix} -1 &{} \tau (\alpha ,\beta ) \\ - \tau (\alpha ,-\beta ) &{} 1 \end{pmatrix}, \qquad \tau (\alpha ,\beta ) = \frac{- \Gamma \left( \frac{\alpha }{2}-\beta \right) }{\Gamma \left( \frac{\alpha }{2}+\beta + 1 \right) },\nonumber \\ \end{aligned}$$

  (A.7)

  and

  $$\begin{aligned} M(z) = \left\{ \begin{array}{l l} \displaystyle e^{\frac{i\pi \alpha }{4} \sigma _{3}}e^{- i\pi \beta \sigma _{3}}, &{} \displaystyle \frac{\pi }{2}< \arg z< \pi , \\ \displaystyle e^{-\frac{i\pi \alpha }{4} \sigma _{3}}e^{-i\pi \beta \sigma _{3}}, &{} \displaystyle \pi< \arg z< \frac{3\pi }{2}, \\ e^{\frac{i\pi \alpha }{4}\sigma _{3}} \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix}, &{} \displaystyle -\frac{\pi }{2}< \arg z< 0, \\ e^{-\frac{i\pi \alpha }{4}\sigma _{3}} \begin{pmatrix} 0 &{} 1 \\ -1 &{} 0 \end{pmatrix},&\displaystyle 0< \arg z < \frac{\pi }{2}. \end{array} \right. \end{aligned}$$

  (A.8)

  In (A.6), $z^{-\beta }$ has a cut along $i{\mathbb {R}}^{-}$, such that $z^{-\beta } \in {\mathbb {R}}$ as $z \in {\mathbb {R}}^{+}$.

  As $z \rightarrow 0$,

  $$\begin{aligned}&\Phi _{\mathrm {HG}}(z) = \left\{ \begin{array}{l l} \begin{pmatrix} {{\mathcal {O}}}(1) &{} {{\mathcal {O}}}(\log z) \\ {{\mathcal {O}}}(1) &{} {{\mathcal {O}}}(\log z) \end{pmatrix}, &{} \text{ if } z \in II \cup III \cup VI \cup VII, \\ \begin{pmatrix} {{\mathcal {O}}}(\log z) &{} {{\mathcal {O}}}(\log z) \\ {{\mathcal {O}}}(\log z) &{} {{\mathcal {O}}}(\log z) \end{pmatrix},&\text{ if } z \in I\cup IV \cup V \cup VIII, \end{array} \right. \nonumber \\&\Phi _{\mathrm {HG}}(z) = \left\{ \begin{array}{l l} \begin{pmatrix} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) \\ {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) \end{pmatrix}, &{} \text{ if } z \in II \cup III \cup VI \cup VII, \\ \begin{pmatrix} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) \\ {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{-\frac{\alpha }{2}}) \end{pmatrix},&\text{ if } z \in I\cup IV \cup V \cup VIII, \end{array} \right. \nonumber \\&\Phi _{\mathrm {HG}}(z) = \begin{pmatrix} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) \\ {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) &{} {{\mathcal {O}}}(z^{\frac{\alpha }{2}}) \end{pmatrix}, \end{aligned}$$

  (A.9)

  where the first, second and third lines read for $\text {Re}\,\alpha = 0$, $\text {Re}\,\alpha > 0$ and $\text {Re}\,\alpha < 0$, respectively.

The unique solution to this RH problem is expressed in terms of hypergeometric functions. Since we will not use the explicit expression of the solution, we will not write it down here. In the case where $\alpha =0$, this RH problem was first solved in [49]. We refer the interested reader to [32, Section 4.2] and [42, Section 2.6] for more details and background on this RH problem for general values of $\alpha$ and $\beta$.