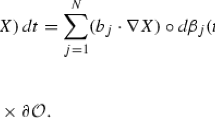Abstract
Our aim is the study of well-posedness for the stochastic evolution equation
for \(T>0\), on a bounded Lipschitz domain \(D \subset \mathbb {R}^d\) with homogeneous Dirichlet boundary conditions, initial values \(u_0\in L^2(D)\), \(p>2\) and \(F:\mathbb {R}\rightarrow \mathbb {R}^d\) Lipschitz continuous. W(t) is a cylindrical Wiener process in \(L^2(D)\) with respect to a filtration \((\mathcal {F}_t)\) satisfying the usual assumptions on a complete, countably generated probability space \((\varOmega ,\mathcal {F},\mathbb {P})\). We consider the case of multiplicative noise satisfying appropriate regularity conditions. By a semi-implicit time discretization, we obtain approximate solutions. Using the theorems of Skorokhod and Prokhorov, we are able to pass to the limit and show existence of martingale solutions. We establish pathwise \(L^1\)-contraction and uniqueness and obtain existence and uniqueness of strong solutions.
Similar content being viewed by others
References
V. Barbu. Nonlinear Differential Equations of Monotone Type in Banach Spaces. Springer, New York 2010.
L. Baňas, Z. Brzeźniak, M. Neklyudov and A. Prohl. Stochastic Ferromagnetism. De Gruyter, Berlin/Boston 2014.
L. Baňas, Z. Brzeźniak, M. Neklyudov and A. Prohl. A convergent finite-element-based discretization of the stochastic Landau-Lifshitz-Gilbert equation. IMA J. Numer. Anal. 34 (2014), no. 2, 502–549.
J. Vovelle F. Berthelin. Stochastic isentropic euler equations. Preprint, 2016. http://math.univ-lyon1.fr/~vovelle/publications.html.
D. Breit. Existence Theory for Stochastic Power Law Fluids. J. Math. Fluid Mech. 17 (2015), 295–326.
Z. Brzeźniak, B. Goldys, and M. Ondreját. Stochastic geometric partial differential equations. In New trends in stochastic analysis and related topics, volume 12 of Interdiscip. Math. Sci., pages 1–32. World Sci. Publ., Hackensack, NJ 2012.
Z. Brzeźniak and M. Ondreját. Weak solutions to stochastic wave equations with values in Riemannian manifolds. Comm. Partial Differential Equations, 36 (2011), no. 9, 1624–1653.
M.G. Crandall. The semigroup approach to first order quasilinear equations in several space variables. Israel J. Math., 12 (1972), 153–163.
C. Dellacherie, P.A Meyer. Probabilités et potentiel. Chapitres V-VIII. Théorie des martingales. Revised edition. Actualités Scientifiques et Industrielles, 1385. Hermann, Paris 1980.
G. Da Prato and J. Zabczyk. Stochastic equations in infinite dimensions. Volume 44 of Encyclopedia of Mathematics and its Applications. Cambridge University Press, Cambridge 1992.
A. Debussche, N. Glatt-Holtz and R. Temam. Local martingale and pathwise solutions for an abstract fluids model. Phys. D 240 (2011), no. 14-15, 1123–1144.
R. E. Edwards. Functional analysis. Dover Publications, Inc., New York 1995.
F. Flandoli and D. Gatarek. Martingale and stationary solutions for stochastic Navier-Stokes equations. Prob. Theory Relat. Fields, 102 (1995), no. 3, 367–391.
A. Garsia, E. Rodemich H. Rumsey. A real variable lemma and the continuity of paths of some Gaussian processes. Indiana Univ. Math. Journal, 20 (1970/71), 565–578.
I. Gyöngy and N. Krylov. Existence of strong solutions for Itô’s stochastic equations via approximations. Probab. Theory Related Fields, 105 (1996), no. 2, 143–158.
M. Hofmanová and T. Zhang. Quasilinear parabolic stochastic partial differential equations: existence, uniqueness. Stochastic Process. Appl. 127 (2017), no. 10, 3354–3371.
M. Hofmanová. Degenerate parabolic stochastic partial differential equations. Stochastic Process. Appl., 123 (2013), no. 12, 4294–4336.
M. Hofmanová and J. Seidler. On weak solutions of stochastic differential equations. Stoch. Anal. Appl., 30 (2012), no. 1, 100–121.
M. Hofmanová and J. Seidler. On weak solutions of stochastic differential equations II. Stoch. Anal. Appl., 31 (2013), no. 4, 663–670.
W. Liu and M. Röckner. Local and global well-posedness of SPDE with generalized coercivity conditions. J. Differential Equations 254 (2013), no. 2, 725–755.
W. Liu and M. Röckner. Stochastic partial differential equations: an introduction. Universitext. Springer, Cham, 2015.
L. Mytnik, E. Perkins, and A. Sturm. On pathwise uniqueness for stochastic heat equations with non-Lipschitz coefficients. Ann. Probab. 34 (2006), no. 5, 1910–1959.
M. Ondreját. Stochastic nonlinear wave equations in local Sobolev spaces. Electron. J. Probab., 15 (2010), no. 33, 1041–1091.
C. Prévôt and M. Röckner. A concise course on stochastic partial differential equations. Volume 1905 of Lecture Notes in Mathematics. Springer, Berlin 2007.
E. Pardoux. Équations aux dérivées partielles stochastiques non linéaires monotones. PhD thesis, University of Paris Sud 1975.
T. Roubíček. Nonlinear Partial Differential Equations with Applications. Springer, Basel 2013.
J. Simon. Compact sets in the space \(L^p(0, T;B)\). Ann. Mat. Pura Appl. 146 (1987), no. 4, 65–96.
J. Simon. Sobolev, Besov and Nikolskii fractional spaces: imbeddings and comparisons for vector valued spaces on an interval. Ann. Mat. Pura Appl. 157 (1990), no. 4, 117–148.
D.W. Stroock and S.R.S. Varadhan. Multidimensional diffusion processes. Springer-Verlag, Berlin/New York 1979.
R. Temam. Navier-Stokes equations. Theory and numerical analysis. North-Holland Publishing Co., Amsterdam/New York/Oxford 1977.
A.W van der Vaart and J.A. Wellner. Weak convergence and empirical processes. Springer, New York 1996.
T. Yamada and S. Watanabe. On the uniqueness of solutions of stochastic differential equations, I, II. J. Math. Kyoto Univ. 11 (1971), 155–167, 553–563.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Vallet, G., Zimmermann, A. Well-posedness for a pseudomonotone evolution problem with multiplicative noise. J. Evol. Equ. 19, 153–202 (2019). https://doi.org/10.1007/s00028-018-0472-0
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-018-0472-0