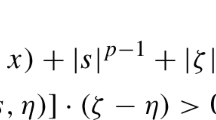Abstract
We consider the weighted parabolic problem of the type
for quite a general class of possibly unbounded weights \( \omega _1,\omega _2\) satisfying the Hardy-type inequality. We prove existence of a global weak solution in the weighted Sobolev spaces provided that \(\lambda >0\) is smaller than the optimal constant in the inequality. The domain is assumed to be bounded or quasibounded. The obtained solution is proven to belong to
Similar content being viewed by others
References
B. Abdellaoui, I. Peral, and M. Walias. Some existence and regularity results for porous media and fast diffusion equations with a gradient term. Trans. Amer. Math. Soc., 367(7):4757–4791, 2015.
C. T. Anh and T. D. Ke. On quasilinear parabolic equations involving weighted \(p\)-Laplacian operators. NoDEA Nonlinear Differential Equations Appl., 17(2):195–212, 2010.
A. Attar, S. Merchán, and I. Peral. A remark on the existence properties of a semilinear heat equation involving a Hardy-Leray potential. J. Evol. Equ., 15(1):239–250, 2015.
P. Baras and J. Goldstein. The heat equation with a singular potential. Trans. Amer. Math. Soc., 284(1):121–139, 1984.
L. Boccardo, A. Dall’Aglio, T. Gallouët, and L. Orsina. Nonlinear parabolic equations with measure data. J. Funct. Anal., 147(1):237–258, 1997.
L. Boccardo, T. Gallouët, and L. Orsina. Existence and nonexistence of solutions for some nonlinear elliptic equations. J. Anal. Math., 73:203–223, 1997.
L. Boccardo and F. Murat. Almost everywhere convergence of the gradients of solutions to elliptic and parabolic equations. Nonlinear Anal., 19(6):581–597, 1992.
L. Boccardo, F. Murat, and J.-P. Puel. Existence of bounded solutions for nonlinear elliptic unilateral problems. Ann. Mat. Pura Appl. (4), 152:183–196, 1988.
M. Bonforte, J. Dolbeault, M. Muratori, and B. Nazaret. Weighted fast diffusion equations (part i): Sharp asymptotic rates without symmetry and symmetry breaking in caffarelli-kohn-nirenberg inequalities. To Appear in Kinet. Rel. Mod., 2016.
M. Bonforte, J. Dolbeault, M. Muratori, and B. Nazaret. Weighted fast diffusion equations (part ii): Sharp asymptotic rates of convergence in relative error by entropy methods. To Appear in Kinet. Rel. Mod., 2016.
H. Brézis and E. Lieb. A relation between pointwise convergence of functions and convergence of functionals. Proc. Amer. Math. Soc., 88(3):486–490, 1983.
A. Dall’Aglio, D. Giachetti, and I. Peral. Results on parabolic equations related to some Caffarelli-Kohn-Nirenberg inequalities. SIAM J. Math. Anal., 36(3):691–716, 2004/05.
B. Franchi, R. Serapioni, and F. Serra Cassano. Approximation and imbedding theorems for weighted Sobolev spaces associated with Lipschitz continuous vector fields. Boll. Un. Mat. Ital. B (7), 11(1):83–117, 1997.
J. P. García Azorero and I. Peral Alonso. Hardy inequalities and some critical elliptic and parabolic problems. J. Differential Equations, 144(2):441–476, 1998.
J. A. Goldstein, D. Hauer, and A. Rhandi. Existence and nonexistence of positive solutions of \(p\)-Kolmogorov equations perturbed by a Hardy potential. Nonlinear Anal., 131:121–154, 2016.
A. Kufner and B. Opic. How to define reasonably weighted Sobolev spaces. Comment. Math. Univ. Carolin., 25(3):537–554, 1984.
S. Merchán, L. Montoro, I. Peral, and B. Sciunzi. Existence and qualitative properties of solutions to a quasilinear elliptic equation involving the Hardy-Leray potential. Ann. Inst. H. Poincaré Anal. Non Linéaire, 31(1):1–22, 2014.
B. Opic and A. Kufner. Hardy-type inequalities, volume 219 of Pitman Research Notes in Mathematics Series. Longman Scientific & Technical, Harlow, 1990.
J. Simon. Compact sets in the space \(L^p(0,T;B)\). Ann. Mat. Pura Appl. (4), 146:65–96, 1987.
I. Skrzypczak. Hardy-type inequalities derived from \(p\)-harmonic problems. Nonlinear Anal., 93:30–50, 2013.
I. Skrzypczak and A. Zatorska-Goldstein. Existence of solutions to a nonlinear parabolic problem with two weights. to appear in Colloq. Math., 2018.
J.-L. Vazquez and E. Zuazua. The Hardy inequality and the asymptotic behaviour of the heat equation with an inverse-square potential. J. Funct. Anal., 173(1):103–153, 2000.
Author information
Authors and Affiliations
Corresponding author
Additional information
Anna Zatorska-Goldstein: The research of AZG has been supported by the NCN Grant No. 2012/05/E/ST1/03232 (years 2013–2017) and by the Foundation for Polish Science Grant No. POMOST BIS/2012-6/3.
Rights and permissions
About this article
Cite this article
Chlebicka, I., Zatorska-Goldstein, A. Existence to nonlinear parabolic problems with unbounded weights. J. Evol. Equ. 19, 1–19 (2019). https://doi.org/10.1007/s00028-018-0465-z
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00028-018-0465-z
Keywords
- Existence of solutions
- Hardy inequalities
- Parabolic problems
- Weighted p-Laplacian
- Weighted Sobolev spaces