On PSO-Based Approximation of Zadeh’s Extension Principle

Abstract

Zadeh’s extension is a powerful principle in fuzzy set theory which allows to extend a real-valued continuous map to a map having fuzzy sets as its arguments. In our previous work we introduced an algorithm which can compute Zadeh’s extension of given continuous piecewise linear functions and then to simulate fuzzy dynamical systems given by them. The purpose of this work is to present results which generalize our previous approach to a more complex class of maps. For that purpose we present an adaptation on optimization algorithm called particle swarm optimization and demonstrate its use for simulation of fuzzy dynamical systems.

The support of the grant “Support of talented PhD students at the University of Ostrava” from the programme RRC/10/2018 “Support for Science and Research in the Moravian-Silesian Region 2018” is kindly announced.

1 Introduction

Zadeh’s extension principle plays an important role in the fuzzy set theory. Mathematically it describes a principle due to which each map $f :X \rightarrow Y$ induces a map $z_f :\mathbb {F}(X) \rightarrow \mathbb {F}(Y)$ between some spaces of fuzzy sets $\mathbb {F}(X)$ (resp. $\mathbb {F}(Y)$) defined on X (resp. Y).

In general the calculation of Zadeh’s extension principle is a difficult task. This is caused mainly by difficult computation of inverses of the map f. Only some cases, e.g. when f satisfies some assumptions like monotonicity, one can find an easier solution. Consequently, the problem of approximation of the image of a fuzzy set $A\in \mathbb F (X)$ under Zadeh’s extension $z_f$ has been attracted by many mathematicians. For example, in [2] and [3] the authors introduced a method approximating Zadeh’s extension $z_f (A)$ which is based on decomposition of a fuzzy set A and multilinearization of a map f. Later in [1] another method using an optimization algorithm applied to $\alpha$-cuts of a chosen fuzzy set was proposed and tested. Further some specific representations of fuzzy numbers have also been used. For example, a parametric LU-representation of fuzzy numbers was proposed and elaborated in [5] and [15]. The authors claim that the LU-fuzzy representation allows a fast and easy simulation of fuzzy dynamical systems and, thus, it avoids the usual massive computational work. However this method is restricted for fuzzy numbers only. Further, the authors of [14] presented another simple parametric representations of fuzzy numbers or intervals, based on the use of piecewise monotone functions of different forms. And finally, another more general procedure allowing to approximate Zadeh’s extension of any continuous map using the F-transform technique was introduced in [9].

We contributed to the problem above in [10] where we introduced an algorithm which can compute Zadeh’s extension of a given continuous piecewise linear map and, consequently, to simulate a fuzzy dynamical system given by this map. We first focused on continuous one-dimensional piecewise linear interval maps and piecewise linear fuzzy sets. These assumptions allowed us to precisely calculate Zadeh’s extension for the class of piecewise linear fuzzy sets, for which we do not necessarily assume even the continuity. This feature should be considered as an advantage of our approach because discontinuities naturally appear in simulations of fuzzy dynamical systems. Still the algorithm proposed in [10] covered a topologically large, i.e. dense, class of interval maps.

The aim of this contribution is to extend the use of our previous algorithm (from [10]) for a more complex class of maps, namely, for the class of continuous interval maps. In order to do this, we intend to linearize a given map f, which is an approximation task leading to an optimization problem (of the determination of appropriate points of the linearization) minimizing the distance between the original function f and its piecewise linear linearization $\tilde{f}$. As there is no feasible analytical solution of the minimization problem, we can approach it from the perspective of the stochastic optimization. For that purpose, we chose the particle swarm optimization algorithm (PSO) that helps us to find appropriate distributions of points in a given space defining piecewise linear approximations as close as possible to the original function f. PSO is one of the most known stochastic algorithms from the group of swarm algorithms. We considered this algorithm due to several reasons. For example, it was the best among algorithms used for a similar task e.g. in [13]. Of course, there are naturally other options to be considered and deeper analysis in this direction is in preparation. Due to page limit we present several preliminary observations only, although we have prepared much more tests.

The structure of this paper is the following. In Sect. 2, some basic terms and definitions used in the rest of this manuscript are introduced. In Sect. 3, we introduce a modification of the original PSO algorithm applied to the problem mentioned in the previous paragraph and then we demonstrate the linearization procedure on a few examples. Further in Sect. 4 we provide a testing of the proposed algorithm, taking into account mainly its accuracy and the choice of parameters. And in the final section (Sect. 5) the proposed algorithm for approximation of Zadeh’s extension is shortly introduced and, finally, the whole process is demonstrated on several examples.

2 Preliminaries

In this subsection we shortly introduce some elementary notions. For more detailed explanation we refer mainly to [8, 9] and references therein.

A fuzzy set A on a given (compact) metric space $(X,d_X)$, where X is a non-empty space (often called a universe), is a map $A :X \rightarrow [0,1]$. The number A(x) is called a membership degree of a point $x\in X$ in the fuzzy set A. For a given $\alpha \in (0,1]$ an $\alpha$-cut of A is the set $[A]_{\alpha }=\{x \in X \mid A(x) \ge \alpha \}.$ Let us remark that if a fuzzy set A is upper semi-continuous then every $\alpha$-cut of A is a closed subset of X. This helps us later to define a metric on the family of upper semi-continuous fuzzy sets on X which will be denoted by $\mathbb {F} (X)$. Note that if X is not compact then an assumption that every $A \in \mathbb F (X)$ has a compact support is required.

Before to define fuzzy dynamical systems it is necessary to define a metric on the family of fuzzy sets $\mathbb {F}(X)$ and such metrics are usually based on the well known Hausdorff metric $D_X$ which measures distance between two nonempty closed subsets of X. For instance, one of the most used metrics on $\mathbb F (X)$ is a supremum metric $d_\infty$ defined as

$$d_\infty (A,B)= \sup _{\alpha \in (0,1]} D_X ([A]_\alpha ,[B]_\alpha ),$$

for $A,B \in \mathbb {F} (X).$ Considering a metric topology on $\mathbb F(X)$ induced by some metric, e.g. by $d_\infty$, we can obtain a topological structure on $\mathbb F (X)$.

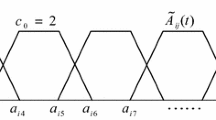
Thus, let X be a (compact) metric space and $f :X\rightarrow X$ be a continuous map. Then a pair (X, f) is called a (discrete) dynamical system. Dynamics of an initial state $x \in X$ is given by a sequence $\{f^n (x)\}_{n \in \mathbb {N}}$ of forward iterates of x, i.e. $x, f(x), f^2 (x)=f(f(x)),f^3(x)=f(f(f(x))),\dots$. The sequence $\{f^n (x)\}_{n \in \mathbb {N}}$ is called a forward trajectory of x under the map f. Now properties of given points are given by properties carried by their trajectories. For instance, a fixed point of the function f is a point $x_0 \in X$ such that $f(x_0) = x_0$. A periodic point is a point $x_0 \in X$ for which there exists $p \in \mathbb {N}$ such that $f^p (x_0)=x_0$. However, usual trajectories are much more complicated as it is demonstrated on Fig. 1.

In this manuscript we deal with a fuzzy dynamical system which admits the standard definition of a discrete dynamical system and, at the same time, forms a natural extension of a given crisp, i.e. not necessarily fuzzy, discrete dynamical system on X. Discrete dynamical systems of the form (X, f) are used in many applications as mathematical models of given processes, see e.g. [11]. Fuzzy dynamical systems studied in this paper are defined with the help of Zadeh’s extension which was firstly mentioned by L. Zadeh in 1975 [17] in a more general context. Later in [7] P. Kloeden elaborated a mathematical model of discrete fuzzy dynamical system $(\mathbb F (X), z_f)$, which is induced from a given discrete (crisp) dynamical system (X, f). This direction was further elaborated by many mathematicians.

Fig. 1.

Trajectories of the dynamical system of a given map, where the initial points are around the value 0.4.

So, formally, let a discrete dynamical system (X, f) be given. Then a continuous map $f :X \rightarrow X$ induces a map $z_f :\mathbb {F}(X) \rightarrow \mathbb {F}(X)$ by the formula

$$(z_{f} (A))(x)=\sup _{y \in {f}^{-1} (x)}\{A(y)\}.$$

The map $z_f$ is called a fuzzification (or Zadeh’s extension) of the map $f :X \rightarrow X$. The map $z_f$ fulfils many natural properties, for instance the following equality $[z_f (A)]_\alpha =f([A]_\alpha )$, for any $A \in \mathbb {F}(X)$ and $\alpha \in (0,1]$, which shows a natural relation to the family of compact subsets ($\alpha$-cuts) of X. It was proved earlier (see e.g. [7] and [8]) that in the most common topological structures on $\mathbb F (X)$ (e.g. for the metric topology induced from the metric $d_\infty$), the continuity of $f :X \rightarrow X$ is equivalent to the continuity of the fuzzification $z_f :\mathbb {F}(X) \rightarrow \mathbb {F}(X)$. Consequently a pair $(\mathbb F (X), z_f)$ fulfils a formal definition of a discrete dynamical system and this dynamical system is called a fuzzy dynamical system. For more information we again refer to [7, 8] and references therein.

3 Particle Swarm Optimization

Particle swarm optimization (abbr. PSO) is an evolutionary optimization algorithm based on stochastic searching in the domain which was originally attributed to R. Eberhart and J. Kennedy in 1995 [4]. The reason of the algorithm, whose behavior is inspired by a social behavior of species, is usually to optimize a given problem. For example, it can be used to find the global optimum of a function of one or more variables. Roughly speaking, population is composed from particles moving around in a given search space according to simple mathematical formulas. In every step of the algorithm, some characteristics (e.g. velocity, the best found solution of every particle, or the best solution in the population) are computed and used to show how the particles move towards the desired solutions. Naturally PSO can stop after a certain number of iterations or after fulfilling some predefined conditions like, for example, accuracy or required size of errors etc. [6, 12, 16].

3.1 Pseudocode of PSO

The aim of this algorithm is an optimization, i.e. searching for a global optima of a function of one or more variables, which is an essential thing in many applications. Initially, a finite number of particles $x_i$ is placed into the domain and each particle is evaluated by a given function. Each particle then determines its movement in the domain, with the help of its historical (personal) best position and of the neighbouring particles combined together with some random parameters.

Below we can see the pseudocode of the original version of PSO which can search for a global optima of a given function. Let $f :\mathbb {R} \rightarrow \mathbb {R}$ be a function for which we search for a global optimum. Now, a number of particles is equal to n and a vector $x=(x_1,\dots ,x_n)$ gives a position of each particle $x_i \in \mathbb R$, $p=(p_1,\dots ,p_n)$ is a vector of the best found positions of each particle in its history, $p_g$ is the best position of a particle from the population called the best neighbour and $v_i$ is a velocity of each particle. Because it is an iterative algorithm, in each iteration, the function f is evaluated in all particles. If the value $f(x_i)$ is better than the previous best value $p_i$, then this point is rewritten as the best point ($p_i:=x_i$) and the value of the function $f(p_i)$ is saved to the value of $p_{best_i}$. The new position of the particles is then reached by updating the velocity $v_i$. Now we can explain the parameters which are used in the equation defining the velocity $v_i$ of the next iteration of a particle position. The elements $U_{\varPhi _1}$, $U_{\varPhi _2}$ indicate random points given by a uniform distribution of each component from intervals $[0,\varPhi _1]$, $[0,\varPhi _2]$, where $\varPhi _1, \varPhi _2 \in \mathbb {R}$. Parameters $\varPhi _1, \varPhi _2$ are called acceleration coefficients, where $\varPhi _1$ gives the importance of the personal best value and $\varPhi _2$ gives the importance of the neighbors best value. If both of these parameters are too high then the algorithm can be unstable because the velocity could grow up faster. Parameter $\chi$ called a constriction factor, multiplies the newly calculated velocity and it can affect the movement propagation given by the last velocity value. The original version of PSO works with $\chi ={2}/({\varPhi -2+ \sqrt{\varPhi ^2-4\varPhi }})$, where $\varPhi =\varPhi _1+\varPhi _2$. The value of this parameter is not changed in time and it has restrictive effect to the result.

• 1. Initialization (functions, variables, constants, ...)

• 2. Cycle - for all i calculate $f(x_{i})$

• 3. Comparison

  • compare $p_{best_i}$ and $f(x_{i})$

  • if $p_{best_i} \le f(x_i)$, then $p_i:=x_i$ and $p_{best_i}:=f(p_i)$

• 4. Best neighbour

  • find the best neighbour of i and assign it j

  • if $f(p_g) \le f(x_j)$, then $p_g:=x_j$ and $f(p_g):=f(x_j)$

• 5. Calculation

  • $v_i:=\chi (v_i+U_{\varPhi _1}(p_i-x_i)+U_{\varPhi _2}(p_g-x_i))$

  • $x_i:=x_i+v_i$

3.2 The Use of PSO for Linearization

This algorithm is an adaptation of the one-dimensional algorithm introduced above to a higher-dimensional case. We have a map given by a formula f(x) and we want to search for a particle, i.e. a vector of $\ell$ points, which gives us the best possible linearization of f. These points indicate a dimension $\ell$ of the problem under consideration and it defines a size of each particle $\mathbf{{x}}$ in the population. Because the idea is to get points (particles) which give us a piecewise linear function, it becomes a problem in which we want to minimalize distances between the original function f and approximating functions given by particles.

The distance between the initial function f and the approximating piecewise linear function is calculated with the help of the following Manhattan metric $d_M$ on a finite number of points D in the domain of f. This metric is given by a function $d_M :\mathbb {R}^D \times \mathbb {R}^D \rightarrow \mathbb {R}$ defined by

$$d_M(\mathbf{{x},\mathbf {y}})= \sum _{i=1}^D |x_{i}-y_{i}|,$$

where $\mathbf{{x}}=\{x_1,x_2,\dots ,x_D\}$ and $\mathbf{{y}}=\{y_1,y_2,\dots ,y_D\}$.

4 Testing

4.1 Parameter Selection

In this subsection we briefly describe the choice of selected parameters and then we study their influence to the accuracy of the proposed algorithm. For each parameter settings the results are calculated 50 times and then evaluated by means of mean and standard deviation.

In general the choice of PSO parameters can have a large impact on optimization performance. In our optimization problem we look for the best setting of the constriction factor $\chi$ and acceleration coefficients $\varPhi _1,\varPhi _2$. If both of the parameters $\varPhi _1,\varPhi _2$ are too high then the algorithm can be unstable because the related velocity could grow up faster. There are some recommendations that can be found in the literature. For example, the authors of the original algorithm [4] recommended the values of $\varPhi _1,\varPhi _2$ to be set to 2.05 and they also recommended the following equation $\varPhi _1+\varPhi _2 >4$ to be satisfied. However, parameter setting can be different model by model and therefore we did it for our purpose as well.

In our testing we set the parameter $\chi \in \{0.57,0.61,0.65,0.69,0.73\}$ and parameters $\varPhi _1,\varPhi _2\in \{1.65,1.85,2.05,2.25,2.45\}$. Thus we have 125 possible combinations of parameters (i.e. 25 combinations for $\varPhi _1,\varPhi _2$ and 5 possibilities for $\chi$). For each of these combinations the proposed algorithm runs 50 times to get the mean and standard deviation from computed outcomes. Some of the initial parameters are fixed - namely, all results are calculated for fixed numbers defining linear parts of approximating function ($\ell =12$), the number of particles in population ($\mathbf{{x}}=25$), the number of iterations of PSO ($I =100$) and the number of points at which the metric $d_M$ is computed ($D =80$). These parameters are chosen only for our testing, therefore for the use of this algorithm it should always be considered what the best initial parameters are for our linearized function. For instance the recommended number of linear parts $\ell$ should definitely be much bigger that the number of monotone parts of the function under consideration to be able somehow cover at least all monotone parts of the approximated function.

4.2 Testing Functions

For the purpose of testing we have chosen functions $g_1,g_2$ given by the following expressions:

$$\begin{aligned} \begin{aligned} g_1(x)=0.9 + (-1 + x) (0.9 + (-0.16 + (5.4 + (-27 + (36 + (510 + \\ (-120 - 2560 (-0.9 + x)) (-0.1 + x)) (-0.6 + x)) (-0.2 + x)) \\(-0.8 + x)) (-0.4 + x)) x), \end{aligned} \end{aligned}$$

$$\begin{aligned} g_2(x)=1/25(\sin 20x+20x \cdot \sin 20x\cdot \cos 20x)+1/2. \end{aligned}$$

Fig. 2.

The graphs of the functions $g_1(x)$ (the left one) and $g_2(x)$ (the right one).

4.3 Parameters Selection

In Tables 1 and 2 below one can see that the choice of parameters $\chi$, $\varPhi _1$, $\varPhi _2$ can affect the results of the linearization procedure. After some preliminary testing on several functions we can provide some introductory observations. Namely, the best setting was found when the constriction factor $\chi$ was taken among values 0.57, 0.61, 0.65 and in a few cases also for the value 0.69. However for $\chi$ lying outside of the interval [0.61, 0.73], the results were much worse and did not meet our expectations. Concerning parameters $\varPhi _1, \varPhi _2$, again, our general observation is that better results are obtained when $\varPhi _1 \ge \varPhi _2$.

It is natural for stochastic methods, that in particular tasks you can get more specific combination of parameters - in the following two tables we emphasize in bold the best 3 combinations of attributes for particular functions $g_1$ and $g_2$. More extensive testing is planned as the continuation of this manuscript.

Table 1. The values of mean and standard deviation for the function $g_1(x)$.

Table 2. The values of mean and standard deviation for the function $g_2(x)$.

4.4 Examples

In this subsection we demonstrate the use of the proposed algorithm on three nontrivial functions $g_1,\ g_2$ and $g_3$, where the first two functions were defined in Subsect. 4.2, and we consider the best settings of random parameters selected in Subsect. 4.3.

Example 1

We have the function $g_1$ whose graph is depicted in Fig. 2. The initial parameters are set to $\chi =0.69, \varPhi _1=2.45,\varPhi _2=1.65$. In our testing we choose $\ell =6, 12, 18$, $I =100$ and $D =80$. This function $g_1$ has 5 monotone parts, thus if our intention is to linearize the function $g_1$ the smallest number $\ell$ to be considered is 6. Naturally, the higher $\ell$ we take, the smoother result we obtain. This is demonstrated on the following figure (Fig. 3).

Fig. 3.

Graphs of the original function $g_1$ (black lines) and the piecewise linear functions (red lines) approximating $g_1$, where $\ell =6,12,18$. (Color figure online)

Example 2

Consider a function $g_2$ (see Fig. 2) and take the initial parameters $\chi =0.69, \varPhi _1=2.45,\varPhi _2=1.65$, $D =80$, $I =100$, $\ell =15,18,25$ (see Fig. 4).

In this example, 14 monotone parts are divided almost equidistantly. Naturally, for better accuracy the number of linear parts should be higher as we can see in the next figure.

Another simple observation is that for better accuracy, it need not help to increase the number of linear parts only, but we need to increase also the number D of discretization points accordingly. To demonstrate this, we choose D to be equal to 200, where $\ell =25$, $\ell =50$ and $I =100$ (see Fig. 5).

Fig. 4.

Graphs of the original function $g_2$ (black lines) and its piecewise linear approximations (red lines), where $\ell =15,18,25$. (Color figure online)

Fig. 5.

Graphs of the original function $g_2$ (black lines) and its piecewise linear approximations of $g_2$ (red lines). (Color figure online)

Example 3

Consider a function $g_3(x)=(x - 1/2) (\sin (1/(x - 1/2))) + 1/2$ (see the picture below). The initial parameters are $\chi =0.69, \varPhi _1=2.45,\varPhi _2=1.65$. In Fig. 6, $\ell =12, 25, 40$, $I =100$ and $D =80$ while in Fig. 7, $\ell =25, 40, 60$, $I =100$ and $D =1000$.

We intentionally consider the function $g_3$ to demonstrate limits of the proposed algorithm because $g_3$ has infinitely many monotone parts at arbitrary small neighborhood of the point 1/2. Consequently, in this case it is not possible to approximate all monotone parts correctly. Despite of this drawback we can see in Figs. 6 and 7 that when we increase the number D of discretization points and the number $\ell$ of linear pairs appropriately, the proposed algorithm works smoothly outside of some neighborhood of the “oscillating” point 1/2.

Fig. 6.

Graphs of the original function $g_3$ (black lines) and the piecewise linear functions (red lines) approximating $g_3$, where $\ell =12,25,40$ and $D =80$. (Color figure online)

Fig. 7.

Graphs of the original function $g_3$ (black lines) and the piecewise linear functions (red lines) approximating $g_3$, where $\ell =25,40,100$ and $D =1000$. (Color figure online)

4.5 Computational Complexity

In this section, we briefly discuss computation complexity of the proposed algorithm. Naturally, the computation time depends on more factors, mainly on the number $\ell$ of linear parts, the number I of iterations, the number D of discretization points and also on computer which is used for compiling. In the table below, we show the time in dependence on number of pairs $\ell$ and number of discretization points $D$, which are the most important parameters for the accuracy of this algorithm. The test was executed on function $g_1$ defined above and with parameters $\chi =0.69, \varPhi _1=2.45$, $\varPhi _2=1.65$ and $I =100$ (Table 3).

Table 3. Computing time in seconds.

5 Approximation of Zadeh’s Extension

5.1 Algorithm

In this subsection we briefly recall an algorithm for calculation of Zadeh’s extension of a given function f. For a more detailed description of this algorithm we refer to [10]. The algorithm in [10] was proposed for one-dimensional continuous functions $f :X\rightarrow X$, i.e. we assume $X = [0,1]$, but one can consider any closed subinterval of $\mathbb R$. The algorithm was proposed for piecewise linear maps f and piecewise linear fuzzy sets A. In this section we demonstrate a generalization of the algorithm from [10] to maps which are not necessarily piecewise linear.

The purpose of the algorithm was to compute a trajectory of a given discrete fuzzy dynamical subsystem $(\mathbb F (X), z_f)$, which is obtained as a unique and natural extension of a given discrete dynamical system (X, f).

Thus we consider a continuous map $f :[0,1] \rightarrow [0,1]$ and a piecewise linear fuzzy set A representing an initial state of induced fuzzy dynamical system $(\mathbb F ([0,1]),z_f)$. First we use the PSO-based linearization (described in Sect. 5) to get an approximated piecewise linear function $\tilde{f}$, and then we use the algorithm from [10] to calculate a trajectory of the initial state A in the fuzzy dynamical system $(\mathbb F ([0,1]), z_{\tilde{f}})$. This simple and natural generalization is demonstrated in the following subsection.

5.2 Examples

Let us see two examples of the procedure described in the previous subsection.

Example 4

Let a function $f_1$ be given by a formula

$$f_1(x)=(-2.9 + (-4.1 + (-15.6 - 14 (-0.8 + x)) (-0.2 + x)) (-0.6 + x)) (-1 + x) x$$

and let A(y) be a fuzzy set depicted on Fig. 8. As the first step of the algorithm we linearize the function $f_1$. For that reason, we use the PSO-based algorithm with parameters $\ell =12, D =80, I =100$. After the linearization process we obtain a piecewise linear function $\tilde{f}_1$ and we can compute a plot containing the first 30 iterations of the fuzzy set A (see Fig. 9).

Fig. 8.

The graph of a function $f_1$ (the left figure, black line) and the linearization of $f_1$ given by PSO (the left figure, red line), the graph of a fuzzy set A (the right figure). (Color figure online)

Fig. 9.

The graphs of $A, z_{\tilde{f}_1} (A),\dots ,z_{\tilde{f}_1}^ {30}(A)$ (the left one) and $z_{\tilde{f}_1}^ {30}(A)$ (the right one).

Fig. 10.

The graph of a function $f_2$ (the left figure, black line) and the linearization of $f_2$ given by PSO (the left figure, red line), the graph of a fuzzy set A (the right figure). (Color figure online)

Fig. 11.

The graphs of $A, z_{\tilde{f}_2} (A),\dots ,z_{\tilde{f}_2}^ {30}(A)$ (the left one) and $z_{\tilde{f}_2}^ {30}(A)$ (the right one).

Example 5

Let a function $f_2$ be given by the following formula $f_2(x)=3.45(x - x^2)$ and A(y) be a fuzzy set depicted in Fig. 10. Again, we need to linearize the function $f_2$. To do this we use the PSO-based algorithm with the following parameters $\ell =18, D =80, I =100$.

Finally we can see a plot of the images of the fuzzy set A for the first 30 iterations (see Fig. 11).

6 Conclusion

In this contribution we generalized our previous algorithm from [10]. The main idea of this algorithm was to calculate Zadeh’s extension for a piecewise linear function and a fuzzy set. Because we restricted our attention only to piecewise linear functions the next natural step becomes a generalization of the previous approach to arbitrary continuous functions. Consequently, we took an evolutionary algorithm called particle swarm optimization and we adapt this algorithm to searching for the best possible linearization of a given function. This naturally extends the use of our previous algorithm of an approximation of Zadeh’s extension, which now gives us an approximated trajectory of the initial state A in a more general fuzzy dynamical system.

The newly proposed algorithm has been briefly tested from several points of view, mainly parameters selection has been taken into account. In our future work we plan more extensive testing involving also computational complexity of the algorithm given by Big O notation which will deal, for example, with the size of the population, number of iterations, number of linear parts, etc. Another natural step is to provide a deep comparison of the original trajectory derived by the Zadeh’s extension with the one given by our algorithm, to provide various comparisons to previously known approaches, and, eventually, to involve, dynamic adaptation of parameters in our PSO-based algorithm. After that, the algorithm should be naturally extended to higher dimensions.