1 Introduction

Crystalline dendrites appear everywhere throughout the natural world in myriad branched forms, as diverse as snow flakes and frost patterns, or as minerals crystallized from solutions and magmas. Dendritic crystals are also prevalent in metallurgical technologies, including alloy casting, primary metals production, welding, and soldering. Dendrites in metallurgy establish the initial microstructures of cast metals and alloys, and are responsible for setting patterns of chemical segregation, crystallographic texture, and grain size developed in these materials. Microstructures, in turn, strongly influence a material’s subsequent mechanical, physical, and chemical behaviors. Moreover, postsolidification treatments—the so-called “downstream processing” of many metallic materials—which ultimately yield both semifinished and final products, are chosen and are affected, to some extent, by the dendritic microstructure.

The descriptive term “dendrite” derives from “\(\delta \epsilon \nu \delta \rho \hbox{o} \nu\)”, a tree, with which its highly branched, arborescent appearance is aptly compared. A dendritic crystal will usually exhibit morphological hints of its underlying crystalline structure and symmetry, as it commonly consists of a primary stem, secondary arms, or side branches, with tertiary branches sprouting from the secondaries—all growing in selected crystallographic directions. It is the continuous generation of all these branches during dendritic solidification that establishes the ramified pattern, length scale, and spatial distributions of all the chemical components and impurities contained in a solidifying melt or solution. These features characterize, if not dominate, the microstructure of most cast alloys.

Relevant to this article is the fact that pure materials also form dendrites if they freeze from their supercooled melts. Pure material dendrites, however, leave no relict chemical variations (segregation) or second-phase eutectic traces behind as a reminder of their active presence during freezing. Instead, most pure metallic melts, if supercooled prior to crystallization, solidify by redistributing the enthalpy steadily between the evolving crystalline dendrites (lower enthalpy phase) and the surrounding melt (higher enthalpy phase). The initial spatial inhomogeneities in the distribution of solid- and liquid-state enthalpies, however, fade away quickly after the completion of solidification, causing such pure “enthalpy” dendrites to vanish into individual grains. Simply stated, the conduction of heat during solidification occurs in the solid-state much more quickly than does the diffusion of segregated chemical species. Despite their ultimate evanescence after complete solidification, dendrites growing in high-purity melts can be observed easily in situ during their active growth stage as shown in Figure 1. The most prominent features revealed in Figure 1 include what seems to be a “steady-state” tip, advancing at constant speed into its surrounding supercooled melt, followed closely by a repeating series of amplifying side branches growing in four directions—up, down, and in and out of the photograph’s focal plane. Farther back from the tip, these closely spaced branches interact and coarsen prior to complete solidification.

Fig. 1
figure 1

In situ micrograph of a succinonitrile dendrite growing from its high-purity supercooled melt. The crystal exhibits a paraboloidal tip followed by a trailing sequence of repeating side branches. The interface mechanism responsible for the repeated growth of these branches is the focus of this study

Full size image

The history of dendrites specific to their application and interest in metallurgy is a long and interesting one, involving their visualization, description, and measurement in many cast materials, as well as the development of a number of hypotheses purporting to explain their origin.[1] A brief review of contemporary theories of dendritic growth now follows, to provide the reader a vantage point for understanding and appreciating the large disparity that has developed between theories of dendritic branching and growth kinetics and actual experimental findings on carefully developed test systems.

A local analysis of interface behavior will then be developed to provide some critically missing physics, which the author will show is essential to understanding the fundamental mechanism of dendritic branching.

2 Dendritic growth theories

2.1 Background

To introduce this section on theories of dendritic growth, I’ll begin with a quote made 20 years ago by Dr. James S. Langer, a prominent physicist who has added much to the theoretical development of this field. His thoughtful reflections address the question of why achieving a fundamental understanding of this complex phenomenon still remains desirable and underscores its special relevance today for metallurgists attempting to improve alloys and cast materials design in general:

Metallurgists have long sought to predict and control alloy microstructures. \(\ldots\) cost effective manufacturing techniques ultimately depend on the precision with which we can solve this problem in non-equilibrium pattern formation. \(\ldots\) we would like to incorporate fundamental understanding of microstructures into computer codes that simultaneously help us design materials with made-to-order properties and optimize their manufacturability and performance.

James S. Langer, Physics Today, October 1992.

Contemporary concepts of dendritic growth trace from the following two important early contributions: (1) the observations made by physicist A. Papapetrou,[2] who accurately described the geometry of a growing dendritic crystal and suggested modeling its shape as an isothermal paraboloid of revolution, the interface of which remains uniformly at its melting point, \(T_m;\) and (2) the follow-up analysis accomplished more than 60 years ago by G.P. Ivantsov, which describes quantitatively the nature of the thermal field surrounding an isothermal needle-like (branchless) dendrite undergoing steady-state growth.[3–5]

Traditionally, the subject of dendritic growth theory is divided into the following two independent components: (1) transport theory, which explains how the large-scale energetics of the \(\ell\rightarrow{s}\) transformation operates and controls the dendrite speed and size, which is mainly credited to Ivantsov and several other investigators who extended his findings to broader classes of dendritic geometries; and (2) interface physics, which captures the underlying microscopic phenomena that are responsible for the branching and directionality that characterize dendritic patterns in real materials. The two theoretical components of dendritic growth have both markedly different histories and status with respect to modern experiments conducted on dendritic growth kinetics and morphologies. We demonstrate in this article that the two components of dendrite theory—transport and interface physics—are not independent aspects at all but remain linked through a subtle effect involving energy transport along the interface.

2.2 Energy Transport

Ivantsov, as well as subsequent investigators of diffusion-controlled phase transformation in more complex geometries,[6] expressed the mathematical solutions for the thermal or diffusion fields that transport heat and/or solute during steady-state freezing in terms of a lumped dimensionless parameter, called the growth Péclet number.Footnote 1

The growth Péclet number P is conventionally defined in such transport problems as

$$ P=\frac{VR}{2\alpha}, $$
(1)

where V and R are the speed of the interface’s advance and its radius of curvature, respectively, and \(\alpha\) is the diffusivity of the melt. Ivantsov’s transport solution relates the dendrite’s growth Péclet number to the melt’s dimensionless supercooling, or supersaturation, defined in this article for the case of a pure melt as \(\Updelta{\vartheta}=(T_{\infty}-T_{{m}})/(\Updelta{H}_{{f}}/C_p).\) Here, \(\Updelta{\vartheta}\) is the dimensionless temperature difference that transports the latent heat and, correspondingly, drives the overall phase transformation kinetics for a solid crystallizing from its pure melt. In the specific case of \(\ell\rightarrow{s}\) transformation, \(T_{{m}}\) is the material’s equilibrium freezing/melting temperature, and \(T_{\infty}\) is the supercooled melt temperature set at some large distance from the heat-releasing dendrite. The scale factor that nondimensionalizes the supercooling \((\Updelta{H}_{{f}}/C_p)\) is the characteristic temperature of the material, given by the ratio of the latent heat of fusion, \(\Updelta{H_{f}},\) to the melt’s specific heat, \(C_p.\) The characteristic temperatures for most metals are typically a few hundred Kelvins, but are much less for the organic test substances discussed subsequently in this article, which are often employed experimentally to check theories.Footnote 2

Ivantsov solved the steady-state energy equation in the melt surrounding an advancing, isothermal, branchless, paraboloidal dendrite and related the dimensionless supercooling to the dendrite’s growth Péclet number, as

$$ \Updelta{\vartheta}=P e^{P}E_1(P) $$
(2)

where \(E_1(P)\) is the first exponential integral, a definite integral. Although Eq. [2] does not have an exact analytic inverse, its formal inverse exposes the relationship between the dendrite’s two dependent variables, V and R, and the independent variable, \(\Updelta{\vartheta},\) namely

$$ V\cdot{R}=2\alpha[{Iv}^{-1}(\Updelta{\vartheta})] $$
(3)

The function \({Iv}^{-1}(\Updelta{\vartheta)}\) appearing in Eq. [3] represents the inverse of Ivantsov’s solution (Eq. [2]). One notes that Eq. [3] relates only the product of the two unknowns of interest as a hyperbolic function of the specified melt supercooling, \(\Updelta{\vartheta}.\) Clearly, finding the unique solution to the dendritic growth problem requires adding an independent equation involving V or R, which is based on physical principles beyond that of conservation and transport of the latent heat of the \(\ell\rightarrow{s}\) transformation. This irrefutable mathematical fact was fully appreciated by Ivanstsov himself and by numerous investigators who attempted to build upon, or modify, Ivantsov’s analysis of the fundamental heat transfer describing steady-state dendritic growth (Eq. [2]).

2.3 Interfacial Physics

Over the last 50 years, several seemingly reasonable ideas were proposed, developed, checked, and ultimately discarded, in attempts to propose the additional physical principle needed to solve the basic dendritic growth problem.[7–24] These efforts included precepts and hypotheses on dendritic interfacial physics as varied as the following:

  1. (a)

    Maximum velocity

  2. (b)

    Interfacial stability

  3. (c)

    Shape self-consistency

  4. (d)

    Minimum entropy production

  5. (e)

    Marginal stability (maximum radius)

  6. (f)

    Selective noise amplification

  7. (g)

    Microscopic solvability

  8. (h)

    Trapped wave theory

  9. (i)

    Maximum entropy production

Take, for example, item (a), the concept of maximum velocity, which would occur, hypothetically, for a paraboloidal dendrite, the solid–liquid interface of which has interfacial energy, i.e., capillarity. As all interfaces have excess free energy, or surface tension, this idea could, conceivably, have provided a reasonable supposition about the operating state of dendrites: namely, that dendrites grow steadily when they achieve their maximum velocity, as allowed by the thermal conduction field and the level of supercooling specified in the melt. Crystal growth at the maximum velocity requires specifically that the dendritic tip radius be just twice the size of the critical radius required for homogeneous nucleation of the solid phase from the supercooled melt. Some early experiments designed to check the validity of this notion, however, showed convincingly that the tip radii of steadily growing dendrites were, in fact, far larger than that required for achieving the maximum velocity. Experiments found that dendrites actually grow with their tip radii more like 100 times the critical radii, and therefore advanced at steady speeds corresponding to only 1 pct of the predicted maximum velocity.[25,26]

The other listed hypotheses for the controlling interfacial physics, unfortunately, also fail to predict dendritic branching behavior, size scale, or growth rates, as determined by quantitative experiments performed on different well-characterized test substances.[26–31] Perhaps most disappointing about these ideas was that the theories based on them proved incapable of providing even qualitative descriptions of the important morphological differences observed among dendritic crystals grown from different substances. As examples, Figure 2 shows a pair of dendrites growing at identical dimensionless supercoolings from different high-purity melts: On the left is shown a dendrite of succinonitrile (SCN), \([\hbox{CN}{-}(\hbox{CH}_{2})_{2}{-}\hbox{NC}],\) a bcc crystal freezing slightly above \(58\,{\deg}\hbox{C},\) and on the right, PVA, \([(\hbox{CH}_3)_3{-}\hbox{C}{-}\hbox{COOH}],\) an fcc crystal that freezes near \(36\,{\deg}\hbox{C}.\) These substances develop individually unique dynamic tip shapes, followed by markedly differing patterns for the orientation, growth rate, and spatial distribution of their side branches. An acceptably useful theory of dendritic growth should be able to describe some of these materials-specific features, including their speed and branching structures, if they are to provide a basis for our fundamental understanding of dendrites and, eventually, be incorporated into engineering casting codes to predict microstructures and segregation patterns in alloys.

Fig. 2
figure 2

Micrographs of cubic dendrites: Left: BCC succinonitrile (SCN), Right: FCC PVA. These dendrites are growing at identical values of the dimensionless supercooling for each material and show distinctive material-dependent features in their growth morphologies. Without a specific interface mechanism accounting quantitatively for the development of side branches, these overall patterns—both their similarities and their differences—can neither be interpreted well using experiments nor predicted accurately through computer simulations

Full size image

2.4 Crystal-Melt Interfaces

Dendrites consist of crystal-melt interfaces only a few atomic or molecular spacings in thickness. This circumstance is treated conveniently with the “sharp-interface” approximation, in which the atomic or molecular transition between crystal and melt is reduced to a geometric surface of zero thickness, to which is assigned an excess energy, composition, and position, in a manner developed for classic models of heterophase interfaces by Gibbs.[32]

Diffuse interfaces, by contrast, are encountered in liquid-vapor systems near their critical points and during solid-state spinodal decomposition of phase-separating supersaturated alloys. Diffuse interfaces may be treated with theories and numerical models that relate to general free energy expansion methods developed originally by Ginzburg and Landau.[33] Free energy expansions deal explicitly with the gradient structures developed between related critical phases and with free energy descriptions that account for structural gradients.[34–37]

Among the sharp interface descriptions postulated for dendritic growth, several approaches still prevail: Some sharp interface models, such as marginal stability,[13] remain in use, as does microscopic solvability, a steady-state theory that also incorporates interfacial energy anisotropy. Numerical simulations of diffuse interfacial structures, based on phase-field models, are now applied widely, and successfully, although approaching the limit of atomically thin interfaces remains computationally challenging.[38–42] Indeed, an array of different simulation methods, including the phase-field model, prove extremely useful for simulating a variety of solid–liquid and solid-state phase transformations.

Moreover, to test any specific hypothesis critically, one must establish a base of quantifiable observations. To date, the most reliable experiments capable of evaluating the predictions derived from theory are those that use test materials that are ultra-pure, stable, and transparent, such as \(\hbox{H}_{2}\hbox{O}\) ice,[25] and plastic crystalline compounds,[26,27–31] such as SCN and PVA. These particular experimental studies each involved observation of these well-characterized molecular substances solidifying from their melts in high-precision thermostats capable of setting small supercoolings accurately that control the kinetics of dendritic crystallization.

In this manner, the two major components of dendritic growth theory could be separated and individually evaluated, as follows: (1) checking the thermal transport field responsible for energy flow during the \(\ell\rightarrow{s}\) phase transformation, viz., testing Ivantsov’s analysis by measuring a dendrite’s growth Péclet number, using the product of \(V\times{R}\) at known supercooling levels, \(\Updelta\vartheta\) (Section II–B); and (2) testing separately some key prediction derived from the interfacial physics that was added to make the theory unique and that allows explicit prediction of either V or R for a specified supercooling.

2.5 Testing Current Theories of Dendritic Growth

The following two theories of dendritic growth are accepted today: (1) marginal stability, developed in the mid-1970s,[13,14] which contends that a dendrite grows at its limit of stability, defined by stochastic fluctuations that continually perturb the dendrite’s tip; and (2) microscopic solvability, a steady-state approach developed in the 1980s that finds unique mathematical solutions (smooth tips) for specified anisotropic capillarity.[16–19] These theories have been checked individually with experiment and were found incapable of predicting the correct scaling laws, growth kinetics, or branching patterns.

The first important experiment that tested microscopic solvability theory studied dendritic growth in SCN and PVA. The results were reported in the early 1990s by Muschol et al.[30] These investigators examined carefully several aspects of microscopic solvability theory. Muschol et al. concluded based on their studies that microscopic solvability was in severe disagreement with their experiments. Quoting their concluding remark, “MST [microscopic solvability theory] in its present form cannot realistically be viewed as being confirmed by experiment”.[30]

Marginal stability and solvability were again subject to an independent sequence of quantitative experiments known as the Isothermal Dendritic Growth Experiment (IDGE). The IDGE series of dendritic growth tests was flown in space by NASA three times, as semiautonomous and ground-based telemetry-controlled experiments aboard the U.S. Space Shuttle Columbia. Three space flights of the IDGE were launched successfully between March 1994, and December 1998 and were carried as part of an experiment complement comprising NASA’s United States Microgravity Payload (USMP) Missions. USMP-2, −3, and −4 collectively yielded growth kinetic and morphological data on ultra-pure SCN and PVA from more than 350 experiments.[43]Footnote 3

Low-earth orbit (LEO) provides a nearly ideal microgravity environment that eliminates all vestiges of buoyant, or natural, convection in the melt during solidification.Footnote 4 Buoyant melt convection is induced in the presence of Earth’s gravity by any heat-emitting dendrite. Achieving slow dendritic growth speeds in either metals or pure test substances demands setting and measuring precisely extremely small supercooling levels in the melt, \(\Updelta{T}\ll1\,\hbox{K},\) which advantageously allows high resolution in situ microphotography, such as displayed in Figures 1 and 2. Convective melt flows alter and complicate the pattern of heat conduction during freezing of high-Prandtl number fluids, particularly at the slow dendritic growth speeds needed in these kinetic experiments. This interference precludes making terrestrial laboratory measurements of a dendrite’s growth Péclet number, which as explained, must be obtained under diffusive, or pure thermal conduction conditions achievable in fluids only in microgravity.Footnote 5

The IDGE series of scientific missions involved precision observations of diffusive dendritic growth speeds, tip radii, and patterns in microgravity.[44–49] Two key discoveries were made, and then verified, by many repeated experiments on different high-purity test materials. First, a quantitative test of Eq. [2] using microgravity data verifies Ivantsov’s analysis of latent heat transport surrounding dendrite tips during dendritic growth. This test of the predicted growth Péclet number versus supercooling was accomplished successfully using dendritic growth experiments performed with high-purity 7-9s SCN. This material was selected because it crystallizes dendritically with a paraboloidal dendritic tip, closely approximating the interface shape assumption made in Ivantsov’s transport analysis. Figure 1 and the left panel of Figure  2 show the steady-state tip structures of SCN dendrites are indeed paraboloids. The product of growth speeds and tip radii data observed simultaneously under both terrestrial and microgravity conditions are plotted in Figure 3 as growth Péclet numbers. Note that only the convection-free data set obtained under microgravity conditions verifies that Ivantsov’s heat conduction analysis for a dendrite tip is correct. These data comprise the first zero-parameter fit of Ivantsov’s analysis.[44] Note also that the terrestrial data included in Figure 1 are influenced by strong buoyancy-induced melt convection and, consequently, do not agree with Ivantsov’s conduction analysis. Second, the theory of marginal stability shows that with increasing supercooling, the dendritic growth speed V increases rapidly, whereas the corresponding tip radius R decreases more slowly. Their combined behavior allows the growth Péclet number, \(P=VR/2\alpha, \) to increase with supercooling, as shown by transport theory (Eq. [2]). However, marginal stability also predicts that the combination \(V\times{R^2}\) should remain constant and be independent of the melt supercooling. More specifically, marginal stability requires that \(2\alpha{d_0}/VR^2\approx1/4\pi^{2}.\) Here, \(\alpha\) is the thermal diffusivity of molten SCN and \(d_0\) is the capillary length of this crystal-melt system.Footnote 6

Fig. 3
figure 3

Log-log plot of the growth Péclet number, \(VR/2\alpha, \) vs melt supercooling \(\Updelta{T}\) for succinonitrile dendrites grown under terrestrial and microgravity conditions. The Ivantsov heat conduction solution which is plotted here as a broken straight line, is based on Eq. [2]. The terrestrial growth Péclet number data expose the considerable influence of terrestrial gravity on heat conduction during crystal growth, whereas the data from dendritic solidification observed in microgravity agree closely with Ivantsov’s transport theory. These data show that classic transport theory describes accurately the major energy field surrounding paraboloidal dendrites[44,45]

Full size image

A direct quantitative check of this dendritic scaling law predicted from marginal stability theory was attempted in the mid-1990s with data from the first two IDGE experiments, both of which used SCN as the test substance. Data from these experiments are plotted in Figure 4 that characterize the observed behavior of SCN dendrites. As shown in Figure 4, the scaling law prediction is not upheld by these measurements. Instead, one observes a well-resolved increase of the quantity \(VR^2\) with increased supercooling. Similar, carefully executed, and multiply repeated experiments, carried out both terrestrially and in microgravity on PVA in the third, and final, IDGE experiment, show more scatter than do the data for SCN and confirm a steady increase of \(VR^2\) with increasing melt supercooling. The conclusion drawn from those PVA dendritic growth data was stated by its authors as follows:

In spite of the large uncertainties in many of the measurements, the scaling parameter [i.e., \(VR^2\) for PVA dendrites] does not appear to be a constant over the full supercooling range of these experiments, and does not appear to agree with current predicted scaling/selection rule values.[49]

Fig. 4
figure 4

Test of the scaling law based on marginal stability theory. The product of simultaneously measured values of dendritic growth speeds in ultra-pure succinonitrile V times the square of the dendrite’s corresponding tip radii R. These data indicate, in contradistinction to the theoretical prediction of a constant value, a clear dependence on the level of melt supercooling. The theoretically predicted scaling relationship, \(V{R^2}=\hbox{const.}\), independent of the melt supercooling, is \(not\) confirmed in these experiments. Original IDGE data were extracted from Ref. 45

Full size image

2.6 Commonality Among Dendritic Growth Theories

A feature found in common among present-day dendritic growth models is that capillarity plays its role by providing the “inner” thermal boundary condition at the solid–liquid interface, to which the “outer” transport field conforms. This restrictive use of capillarity remains the case whether a model is based on noise-mediated pattern development, as in marginal stability theory, or seeks a solution based on steady-state solvability. Thus, the Gibbs-Thomson equilibrium boundary condition merely replaces the isothermal interface boundary condition originally assumed by Ivantsov. Moreover, application of capillarity as the temperature boundary condition on the solid–liquid interface comprises the identical methodology used since the earliest models of dendritic growth were considered over 50 years ago.[7,8]

In the next section, we show that the Gibbs-Thomson capillarity effect is much more than just a boundary condition on the surrounding transport field. Capillarity introduces temperature gradients along a dendritic interface—albeit extremely weak ones—so that the Gibbs-Thomson equilibrium temperature distribution acts as an independent energy field during crystal growth, producing, as we shall demonstrate, more important effects on the branching process than recognized previously.

3 Capillarity

3.1 Background

Interfacial energy effects during crystal growth, or capillarity, are such that the equilibrium temperature between a crystal and its melt, at a fixed pressure, varies slightly with the local interfacial curvature. Specifically, the equilibrium interface temperature is depressed imperceptibly (by a few milli-degrees below \(T_{{m}}\)) near a highly curved dendrite tip and is slightly elevated—and thus closer to \(T_{{m}}\)—at locations farther away from the tip, where the interface is somewhat flatter. As mentioned at the end of Section II–B, standard models of dendritic growth view such paltry capillary fields as energetically irrelevant because they appear, at least superficially, to be inconsequential when compared with the (Ivantsov) transport field that governs the overall energetics of the \(\ell\rightarrow{s}\) transformation. This view is certainly not unreasonable, as the Ivantsov field, acting normal to the growing crystal-melt interface, spans a temperature difference in the melt that is several orders of magnitude greater than the Gibbs-Thomson field along the interface. Furthermore, it may be argued that any thermal fluxes that happen to be associated with the gradients produced by the equilibrium temperature distribution itself are themselves confined to act tangentially along the interface. Thus, such weak gradients could not, in any event, assist in the energy transport directly affecting the rate of \(\ell\rightarrow{s}\) transformation. For these apparently cogent reasons, the Gibbs-Thomson temperature distribution remains today solely as a passive boundary condition in standard models of dendritic growth. As shown next, however, capillarity also plays a more subtle role, which has been overlooked, in the initiation and control of dendritic branching.

3.2 Gibbs-Thomson as an Energy Field

Conventional thinking notwithstanding, the Gibbs-Thomson temperature distribution was reconsidered as a full-fledged energy field after the present author analyzed experiments conducted on the melting kinetics of needle-like crystallites. These crystallites were suspended in their melt under microgravity conditions and exhibited the puzzling behavior of suddenly becoming more spherical as they decreased in volume to sufficiently small size prior to their complete extinction by melting.[50,51] It was shown recently that the observed onset of spheroidization was caused by the unexpected appearance during melting of heat currents generated internally to the crystallites. The “extra” energy for spheroidization arose through the action of interfacial capillarity when the needle-shaped crystallites melted down to sufficiently small sizes.[52,53] This unusual finding, which was discovered in experiments on melting crystals, prompted the present reexamination of the role played by the Gibbs-Thomson temperature distribution for the case of freezing.

A brief summary of this interface analysis and its further implications on understanding the mechanism of dendritic branching follow.

3.3 Tangential Fields

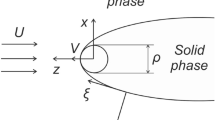
We examine a simple two-dimensional dendritic interface, chosen in the form of a semiellipse, with its semimajor x-axis, a, longer than its shorter semiminor y-axis, b. This provides a slender, finger-like starting shape suitable for a dendrite. Figure 5 shows the interfacial configuration.

Fig. 5
figure 5

An elliptically shaped dendritic interface. The tangential Gibbs-Thomson equilibrium temperature field, \(T_{{int}}(\varphi), \) and the Ivantsov transport field act simultaneously over the crystal-melt interface as indicated schematically. Also shown are the dimensionless space coordinates, \(\mu=x/a\) and \(\eta=y/a, \) the unit normal vector on the interface \({\bf n}\) and its normal angle \(\varphi,\) and the tangent vector \(\sigma\) directed along the curved interface

Full size image

It proves convenient subsequently to scale the coordinates of the crystal-melt interface in units of the semimajor axis a, so that the scaled coordinates \(x/a\equiv\mu,\) and \(y/a\equiv\eta\) define dimensionless coordinate axes for the starting shape. The equation of the ellipse transforms to

$$ \eta=\frac{b}{a}\sqrt{1-\mu^2}. $$
(4)

The presence of an Ivantsov-type transport field suggests the normal flow of latent heat away from the crystal-melt interface during subsequent freezing. The Gibbs-Thomson temperature distribution \(T_{{int}}(\varphi)\) represents the instantaneous distribution of equilibrium temperatures along the semi-ellipse, with the tip region at \(\mu=1\) slightly cooler than the temperature at the equator \(\mu=0.\) We will treat the simpler case of isotropic capillarity in this article. Anisotropic interfacial energy, although extremely important in real dendritic crystal patterns, complicates the current analysis and makes only minor differences in what we wish to demonstrate in this study about the fundamental mechanism of branching.

The equilibrium interfacial temperature along the crystal-melt interface is expressed by the Gibbs-Thomson Eq. [1]

$$ T_{{int}}(\varphi)=T_{{m}}-\left(\frac{\gamma_{s\ell}}{\Updelta{S_{f}}/\Upomega}\right) \kappa(\varphi) $$
(5)

where \(\gamma_{s\ell}\) is the crystal-melt interfacial energy density, \(\Updelta{S_{f}}=\Updelta{H_{f}}/T_{m}\) is the molar entropy of fusion, \(\Upomega\) is the molar volume of the melt, and \(\kappa(\varphi)\) is the ellipse’s curvature function. The angle \(\varphi\) appearing in Eq. [5] is the local normal angle on the interface, which depends on the location \((x, y)\) or \((\mu, \eta).\) The small negative temperature shift, \(T_{{int}}-T_{{m}},\) which is caused by interface curvature, can be scaled into an interface potential \(\vartheta(\varphi),\) as the dimensionless Gibbs-Thomson equation,

$$ \vartheta(\varphi)=\frac{T_{{int}}-T_{m}}{\Upgamma/a}=-a\kappa({\varphi}) $$
(6)

where \(\Upgamma/{a}=a^{-1}\left(\frac{\gamma_{s\ell}}{\Updelta{S_{f}}/\Upomega}\right)\) is the capillary constant scaled by the semimajor axis a, which bears the physical unit [K].

The Gibbs-Thomson capillary temperature field expressed through Eq. [5], and its associated interfacial thermodynamic potential, \(\vartheta(\varphi)\) (Eq. [6]), imply that weak gradients develop and energy travels along the interface “flowing” from higher to lower potential. The gradients caused by this capillary field are found by calculating the tangential derivative of the interface potential, which is directed along the arc length of the curved interface. The gradient vector field of the Gibbs-Thomson distribution is

$$ \varvec{\nabla}_{\sigma}[\vartheta(\varphi)]= -a\varvec{\nabla}_{\sigma}[\kappa(\varphi)]= -\varvec{\nabla}_{\sigma}[\hat\kappa(\varphi)] $$
(7)

where \({\varvec\nabla}_{\sigma}[\ \ ], \) is the tangential vector gradient operator, and \(\sigma\) denotes a dimensionless unit vector that is parallel to the interface and pointing toward the tip. The second equality in Eq. [7] expresses the interfacial potential gradient in terms of the dimensionless curvature, which is defined as \(\hat\kappa(\mu)\equiv{a}\kappa(\mu).\)

The dimensionless curvature of an ellipse \(\hat\kappa(\mu)\) is the following function of \(\mu{:}\)

$$ \hat\kappa(\mu)=\frac{b}{a(1-\mu^2)^{\frac{3}{2}} \left(1-\frac{b^2\mu^2}{a^2(-1+\mu^2)}\right)^{\frac{3}{2}}} $$
(8)

for which the normal angle on the interface remains positive on the upper half-plane \(\eta>0\) and negative on the lower half-plane \(\eta<0.\) The normal angle \(\varphi\) and the scaled \(\mu\)-coordinate are with this sign convention everywhere related as

$$ \varphi(\mu)=\pm\left(\arctan\left[\frac{-b\mu}{a\sqrt{1-\mu^2}}\right] +\frac{\pi}{2}\right) $$
(9)

See again Figure 5. The distribution of the Gibbs-Thomson interface potential along an elliptical interface is

$$ \vartheta(\mu)=-\frac{b}{a}\left[(1-\mu^2) \left(1-\left(\frac{b}{a}\right)^2 \left(\frac{\mu^2}{-1+\mu^2}\right)\right) \right]^{-\frac{3}{2}} $$
(10)

For specificity, a 3:1 ellipse is chosen so the semiaxes in Eq. [10] assume values a = 3 and b = 1. The interface potential distribution \(\vartheta(\mu),\) is plotted for this elliptical shape in Figure 6. The potential is negative everywhere and remains close to zero for almost half the distance along the semiellipse from the equator to tip. The potential then decreases rapidly as the tip at \(\mu=1\) is approached. One expects from this potential distribution relatively slowly increasing energy fluxes near \(\mu=0\) and stronger, variable fluxes toward the tip as energy flows down, and proportionately, to the local gradient. The vector gradient field caused by the Gibbs-Thomson potential distribution on an ellipse may be shown to be the following function of \(\mu{:}\)

$$ \varvec{\nabla}_{\sigma}\left[\vartheta(\mu)\right]= \frac{3ab(-a^2+b^2)\mu}{\sqrt{1-\mu^2}(a^2+(-a^2+b^2)\mu^2)^2 \sqrt{1-\frac{b^2\mu^2}{a^2(-1+\mu^2)}}}\cdot\sigma $$
(11)

The associated energy flux vector \(\Upphi(\mu)\cdot\sigma\) [watts/m] on the interface is determined with Fourier’s law

$$ \Upphi(\mu)\cdot\sigma=-\left(k_{{int}}\frac{\Upgamma}{a^2}\right) \varvec{\nabla}_{\sigma}\left[\vartheta(\mu)\right] $$
(12)

in which the interface conductivity, \(k_{{int}},\) appearing in Eq. [12], bears the units [watts/K].Footnote 7

Fig. 6
figure 6

Upper: Distribution of the Gibbs-Thomson interface potential vs \(\mu=x/a\) for a 3:1 semielliptical crystal. The interface remains below its thermodynamic melting temperature \((\vartheta=0)\) everywhere, especially approaching the curved tip region. The maximum decrease in actual interface temperature [K] would amount to only a few millidegrees. Middle: Tangential energy flux magnitude, \(\hat\Upphi_{\sigma}, \) caused by gradients in the Gibbs-Thomson distribution. The flux increases toward a distinct peak before decreasing and reversing direction close to the tip. This energy flux is driven by the tangential gradients of the interface potential function plotted in the upper diagram. Lower: Normal flux magnitude associated with energy conservation on the interface. Energy accumulation on the interface is the (negative) divergence of the tangential capillary flux vector

Full size image

The flux vector defined in Eq. [12] may be nondimensionalized as

$$\hat\Upphi_{\sigma} (\mu)\cdot\sigma= \frac{\Upphi (\mu)}{k_{{int}}\Upgamma/a^2}\cdot\sigma$$
(13)

Again, for the illustrative case of a 3:1 ellipse, the dimensionless energy flux magnitude \(\hat\Upphi(\mu)\) traveling over the interface is plotted in Figure 6, middle. This flux magnitude is given by the expressions

$$\hat\Upphi_{\sigma}(\mu)=-\varvec{\nabla}_{\sigma}\left[\vartheta(\mu)\right]\cdot {\sigma}=\frac{27\mu(-23+24\mu^2)}{\sqrt{1-\mu^2}(-9+8\mu^2)^3} $$
(14)

The tangential interfacial energy flux increases slowly with distance along the flatter regions of the interface and rises to a sharp peak located almost 90 pct of the way to the tip. As the tip is approached even more closely and \(\mu\rightarrow1,\) the flux suddenly decreases and reverses direction.

3.4 Interfacial Energy Conservation

The temperature variations caused by capillarity are extremely small and generally do not exceed a few millidegrees. This extreme weakness notwithstanding, the autonomous energy fluxes associated with capillarity must still be conserved locally at every point along the interface. The tangential fluxes along the 3:1 elliptical interface are shown in Figure 6-middle. A standard method for evaluating local energy conservation is to calculate the “convergence” of the tangential heat flux vectors on the interface, \(\hat\Upphi(\mu)\cdot\sigma,\) or equivalently, to calculate the divergence of the gradient at each point.

The divergence of the potential’s gradient field for a 3:1 ellipse, given by Eq. [11], is defined by standard vector calculus expressions, namely

$$ \varvec{\nabla}_{\sigma}\cdot\varvec{\nabla}_{\sigma}\left[\vartheta(\mu)\right] =-\nabla_{\sigma}[\hat\Upphi(\mu)], $$
(15)

where the RHS of Eq. [15] is (minus) the divergence of the dimensionless interface flux. Interface energy conservation may be stated mathematically through the following local balance

$$ \left(\frac{k_{{int}}\Upgamma}{a^3}\right)\nabla_{\sigma}[\hat\Upphi_{\sigma}(\mu)] +\left( \frac{C_{p_{{int}}}\Upgamma}{a}\right)\frac{\partial[\vartheta(\varphi)]}{\partial{t}} - \Upphi_{n}(\mu)=0, $$
(16)

the first term in Eq. [16] is the net energy deposited, or removed, at a point on the interface by the divergence of its tangential flux or potential gradient; the second term, is proportional to the interfacial heat capacity, \(C_{p_{{int}}} \left[ \text{J}/\text{m}^2 - \text{K} \right]\) if the interfacial heat capacity is non-zero; and the third term is the capillary-induced normal flux leaving the interface, directed either into the crystal or the melt. These energy terms must balance at every point along the crystal-melt interface, and account for the Gibbs-Thomson energy. The effect of the normal fluxes is to increase, or decrease, slightly, the large thermal gradients surrounding the interface from the Ivantsov transport field, which is primarily responsible for setting the local freezing rates.

Dividing through Eq. [16] by the leading coefficient, (k int Γ/a3), yields a fully dimensionless interface conservation equation for the Gibbs-Thomson energy field,

$$ \nabla_{\sigma}[\hat\Upphi_{\sigma}(\mu)] + \frac{\partial[\vartheta(\varphi)]}{\partial{\tau}} - \hat\Upphi_{n}(\mu)=0, $$
(17)

where the dimensionless interface time, τ, is physical time divided by the interfacial diffusion time, \(C_{p_{{int}}} a^2/ k_{int},\) and the dimensionless normal flux is defined here as \(\hat\Upphi_{n}(\mu) = \Upphi_{n}(\mu)\left(a^3/ k_{int}\Upgamma\right).\) The capillary-related heat flux released at a point from such an interface is directed normal to the interface either toward the crystal or toward the melt—depending on the sign of the divergence of the Gibbs-Thomson tangential flux. The direction of this normal heat flux at any point must also be selected in accord with the Le Chatelier-Braun principle.

Most importantly, this normal capillary flux either slightly retards, or slightly increases, the local freezing rate. One notes that if directed toward the crystal, the normal flux causes a slight retardation of the freezing rate, whereas if directed toward the melt, then the normal flux causes a slight local increase in the freezing rate. Substituting Eq. [15], then Eq. [7], for the first term in Eq. [17], which is the tangential flux, and eliminating the second term, by assuming a zero interfacial heat capacity for the interface, yields the normal flux that satisfies local interface energy conservation. Perhaps most surprising is that this normal flux equals the surface Laplacian of the Gibbs-Thomson potential, and for isotropic surface energy, also equals the negative surface Laplacian of the interface curvature, namely,

$$\hat\Upphi_{n}(\mu) = \nabla^2_{\sigma}[\vartheta(\mu)]=\nabla^2_{\sigma}[\hat k(\mu)], $$
(18)

Evaluating Eq. [18] explicitly for a 3:1 ellipse one finds that the normal flux is

$$ \hat\Upphi_{n}(\mu) = - \frac{243(69-152\mu^2+256\mu^4)}{(9-8\mu^2)^{\frac{9}{2}}}.$$
(19)

Equation [19] is plotted in Figure 6 lower. Where the normal capillary flux has a positive sign (0 ≤ μ ≤ 0.95) it is directed toward the melt, and proportionately increases the local rate of freezing. The flux magnitude falls precipitously from its peak value near μ = 0.9, reversing sign just below μ = 0.95, where the energy becomes redirected toward the crystal and retards the rate of freezing.

It is interesting and important to note that the capillary-mediated modulation of the local freezing rates from point to point along an interface, as demonstrated in Figure 6, occurs autonomously by tangential heat fluxes arising from the gradients of the Gibbs-Thomson energy field.

3.5 Le Chatelier-Braun Responses

Now, a crystal-melt interface on which heat energy is being added or withdrawn from point to point is an example of what Van’t Hoff termed mobile equilibrium.[55] The local response of such a system to capillary-induced autonomous energy changes is predicted by the Le Chatelier-Braun effect, the fundamental basis for which is the combined 1st and 2nd laws of thermodynamics.[56–59] The Le Chatelier-Braun effect posits[55,60] that mobile systems respond by negative feedback to imposed extensive variable changes. In this instance, the changes involve the autonomous addition or loss of energy from the Gibbs-Thomson field.

Viewed the other way round, the Le Chatelier-Braun effect also states that mobile systems must respond to intensive variable changes (rising or falling potential) in a manner so as to increase the corresponding change in the conjugate extensive variable, which is the energy or entropy added or released along the interface. These countervailing descriptions cause confusion about the Le Chatelier-Braun effect and, consequently, were distinguished by Paul Ehrenfest in his explanation of this peculiar dichotomy, as either Widerstandfähigkeit (capable of resisting) or Passungsfähigkeit (capable of adopting).[61] Both of these descriptions are, however, thermodynamically correct and equivalent, and will be used to determine the direction of the energy fluxes normal to the interface added by capillarity.

4 Kinematic Rotation

The opposing freezing responses caused by the normal flux as it vanishes surrounding the root location on the interface (See Figure 6-Lower) sharpen and flatten the adjacent locations simultaneously. Simultaneous yet opposite changes in curvature occurring at a point on the interface induce localized rotation, or tilting, of the nearby interface orientations. Figure 7 shows a schematic that interprets how the influence of a zero in the instantaneous rates of freezing stimulates a change in local interface orientation. The local analysis provided in this study points out where the interface will rotate autonomously: namely where the surface Laplacians of the potential, or curvature, vanish, and where the interface freezing rate is retarded on one side, and accelerated on the other.

Fig. 7
figure 7

Influence of a zero in the time rate of change of freezing at a location \(\varphi^{\star},\) where the surface Laplacians of the potential, or curvature, vanish. See again the root location of the normal flux in Fig. 6-Lower. The middle panel suggests that simultaneous opposing tendencies to sharpen from cooling and flatten from heating, combine, and induce a wave-like ripple or wrinkle of the interface. The right panel suggests that the interface wrinkle, once formed, couples to the strong external transport field in the adjacent melt and eventually develops into a dendritic side branch. This process repeats itself over and over near the tip as the dendrite advances

Full size image

5 Dynamic Verification of Kinematic Rotation

The dynamic behaviors of the 3:1 ellipse discussed previously, as well as that for a 2:1 ellipse, were checked independently using a low-noise integral equation solver developed by Lowengrub and Li.[62] This solver can evolve accurately simulated diffusion-limited dendrites and other interesting patterns such as fluid-fluid interpenetrating Saffman-Taylor “viscous fingers”[63,64] observed in Hele Shaw cells.[65–68] In the current study, the solver provides numerical solutions to Laplace’s equation tracking the thermal field surrounding the evolving dendritic pattern and follows the interface as it develops over time with the main transport field. The boundary condition applied on the solid–liquid interface is the Gibbs-Thomson equilibrium temperature distribution Eq. [5] which reflects both the instantaneous value of the interface curvature and the presence of interfacial energy.

The predicted location of the rotation points, which are determined analytically on these starting shapes, may be compared with their dynamically evolved positions as observed with the solver. The analytically determined value for the initial root position and corresponding rotation point for a 3:1 semi ellipse with isotropic interface energy is \(\mu_{{local}}^{\star}=0.9878. \) The actual rotation point observed independently with the dynamical solver occurs at \(\mu_{{global}}^{\star}=0.9877. \) These rotations correspond to the dimensional location \(x^{\star}\approx2.96, \) which occurs close to the tip position at x = 3.

In a second case tested with a 2:1 ellipse and isotropic interface energy, the analytically determined root and rotation point position was \(\mu_{{local}}^{\star}=0.9688, \) which compares well with the first rotation point observed through dynamic evolution at \(\mu_{{global}}^{\star}=0.9687. \) These positions correspond, respectively, to the dimensional interface position at \(x^{\star}\approx1.94, \) which is again near the ellipse’s tip at x = 2. We note that with isotropy of the interface energy, the initial rotation points of those elliptical shapes occur within approximately 2 to 3 pct of the tip positions of the ellipses.

Adding a small amount of interface energy anisotropy draws the position of the initial rotation point away from the tip. Figure 8 shows these results as an overlay of an undistorted 2:1 ellipse and a frame taken from the dynamic solver at an early time. This starting shape had 0.5 pct 4-fold energy anisotropy along its interface. The rotation points developed by these superposed shapes show up clearly at the predicted dimensional location of \(x^{\star}\approx1.70, \) which is within approximately 15 pct of the tip location.

Fig. 8
figure 8

Dynamical check of the kinematically predicted initial rotation points for a 2:1 ellipse with 0.5 pct 4-fold energy anisotropy. Left panel: Normal flux produced by capillarity vs distance x showing the analytically predicted rotation point at \(x^{\star}=1.697.\) Where the flux is positive, it accelerates freezing, and where it is negative it retards freezing. Right panel: An early video frame taken from the dynamic simulation of a 2:1 elliptical interface with 0.5 pct 4-fold energy anisotropy. The coordinates \(x^{\star}=1.697\) of the predicted location of the initial rotation based on local response theory (left panel) is confirmed independently at \(x^*\approx1.70\) by observing evolution in the dynamic solver. These responses are predicted by local analysis of interfacial energy conservation and the LeChatelier-Braun effect. These interface changes may be observed directly here from the overlay of the starting 2:1 half-ellipse, which is shown as the dashed curve, with the displayed video frame

Full size image

Thus, the tangential component of the fluxes produced from the Gibbs-Thomson field exhibits a divergence that causes the interface to both accelerate slightly and be retarded locally. The response of the interface, as discussed in Section III–E, results in slightly altered rates of freezing along the crystal-melt interface. Where the rate of change of the freezing rate vanishes, the interface starts to rotate. A “wrinkle” develops near the rotation point as the interface couples to the outer normal field and grows rapidly into a branch. The tip meanwhile advances and alters its shape dynamically from that of the starting ellipse. That shape change eventually induces yet another rotation with subsequent branch formation. Up to four onsets of interface rotation have been observed dynamically near the tip, each occurring sooner than the previous one. Figure 9 shows the dynamic evolution of the 2:1 ellipse and suggests how a series of kinematic rotations can evolve into a highly ramified dendritic pattern.

Fig. 9
figure 9

Selected video panels extracted from several hundred frames generated by the dynamic solver, showing longer time evolution of a 2:1 elliptical starting shape with some interface energy anisotropy into a noise-free branched pattern. The pairs of dots indicate the positions of rotations occurring during pattern evolution. The initial panel in this time sequence (frame 0) was overlaid in Fig. 8-right with a second evolved panel (Frame 49). This confirms the predicted initial rotation points and exposes the adjacent regions of flattening and sharpening. Subsequent rotation points can be predicted by using a global interface energy analysis, which is not discussed in this study, and checked independently with the dynamic solver, which shows that they couple to the external field and amplify into branches

Full size image

6 Summary and Conclusions

This study reviewed theories of dendritic crystal growth and, citing pertinent experimental studies, showed that current dendrite theories fail to predict observed phenomena properly. The common thread among all theories of dendrite formation is their restricted use of capillarity, namely, how the Gibbs-Thomson effect is applied to the interface. The Gibbs-Thomson temperature distribution on a curved dendritic interface consists of an extremely weak variation from the curved tip region to the flatter regions away from the tip. Specifically, the equilibrium temperature variation spans only a few millidegrees in totality. This tiny range of temperature—compared with the more robust Ivantsov transport field that surrounds the dendrite—has traditionally relegated the Gibbs-Thomson temperature distribution as an interface boundary condition on the external field. The new view taken here is that the equilibrium temperature distribution is an active interface energy field, albeit it an extremely weak one. As such, capillarity acting on a crystal interface, which is well away from from its equilibrium configuration, produces energy gradients and fluxes and, consequently, divergences of those weak vector fields.

A reexamination of the consequences of a weak energy field along the crystal-melt interface revealed that additional capillary heat fluxes either increase or retard the local freezing rate, and where they vanish interface rotation occurs. The Le Chatelier-Braun principle—a consequence of the laws of thermodynamics—requires a response from the mobile interface to the weak fluxes induced autonomously by the Gibbs-Thomson energy field. We find that curved regions near the tip of an elliptical interface will warm, and be retarded, so they respond by flattening, whereas flatter regions will cool, and accelerate, so they respond by sharpening. Where the incipient processes of flattening and sharpening become adjacent, the interface undergoes a rotation, by tilting and enhancing the exterior local temperature gradients in the melt. This action couples the interface to the surrounding transport field and results in branch formation.

A low-noise dynamic solver verifies the locations of the initial rotation points, which depends sensitively on both the interface shape and the anisotropy of the interfacial energy. The full details of these dynamic tests will be reported elsewhere. Dynamic solver studies also allow the observation of subsequent rotation points that occur episodically at locations near the tip, the shape of which changes over time. (The location of subsequent rotation points cannot be found just using the current local analytical theory.) Eventually, the tip develops an appropriate “steady” tip shape that leads to a synchronicity between the occurrence of kinematic rotations and the tip advancement. These act in concert as a nonlinear limit cycle. Once established, the dendrite’s limit cycle produces the classic branching pattern.

Thus, we conclude, capillarity-induced rotation provides the fundamental deterministic mechanism responsible for dendritic branching. Specifically, rotation occurs where the surface Laplacians of the Gibbs-Thomson potential and the interface curvature vanish. These are equivalent statements when the interfacial energy is isotropic. Selective noise amplification, marginal stability, or other stochastic phenomena do not enter the process at this early stage or seem to play any direct role in pattern-forming dynamics, per se. Some aspects concerning how the rotation couples with the exterior transport field have yet to be resolved and are part of an ongoing analysis of global energy conservation on near-equilibrium interfaces. Certainly more computer-based dynamic testing and new experiments on well-characterized materials are called for to test these ideas more critically and perhaps to achieve a deeper understanding of their implications for predicting cast microstructures.