Generalised Central Limit Theorems for Growth Rate Distribution of Complex Systems

Abstract

We introduce a solvable model of randomly growing systems consisting of many independent subunits. Scaling relations and growth rate distributions in the limit of infinite subunits are analysed theoretically. Various types of scaling properties and distributions reported for growth rates of complex systems in a variety of fields can be derived from this basic physical model. Statistical data of growth rates for about 1 million business firms are analysed as a real-world example of randomly growing systems. Not only are the scaling relations consistent with the theoretical solution, but the entire functional form of the growth rate distribution is fitted with a theoretical distribution that has a power-law tail.

Appendices

Appendix A: Random Multiplicative Processes

Because random multiplicative processes are not widely known, here we introduce a simple exactly solvable case of a random multiplicative process and show intuitively how the process realises a power-law distribution in the statistically steady state. Further, a continuum-limit version of this multiplicative process is discussed. We consider a positive random variable, $x(t)$, that follows the following stochastic equation:

$$\begin{aligned} x(t+\Delta t)=g(t)x(t)+1, \end{aligned}$$

(14)

where $g(t)$ is a stochastic noise term that takes either a positive constant, $g$, or $0$ with probability $1/2$, respectively. Starting with the initial condition, $x(0)=1$, the time evolution is given as

$$\begin{aligned} x(\Delta t)= \left\{ \begin{array}{ll} g+1 &{} (\text {prob}. \quad 1/2), \\ 1 &{} (\text {prob}. \quad 1/2), \\ \end{array} \right. \;x(2 \Delta t)= \left\{ \begin{array}{ll} g^2+g+1 &{} (\text {prob}. \quad 1/4), \\ g+1 &{} (\text {prob}. \quad 1/4), \\ 1 &{} (\text {prob}. \quad 1/2), \\ \end{array} \right. \quad \cdots .\quad \end{aligned}$$

(15)

The general solution at time step $\tau$ is obtained as

$$\begin{aligned} x( \tau \Delta t)= \left\{ \begin{array}{ll} (g^\tau -1)/(g-1) &{} (\text {prob}. \quad 1/2^\tau ), \\ (g^{\tau -1}-1)/(g-1) &{} (\text {prob}. \quad 1/2^\tau ),\\ \vdots &{} \\ (g^{k}-1)/(g-1) &{} (\text {prob}. \quad 1/2^k), \\ \vdots &{} \\ 1 &{} (\text {prob}. \quad 1/2), \\ \end{array} \right. \end{aligned}$$

(16)

where $k$ is an integer from $1$ to $\tau$. From this solution, we can calculate the cumulative distribution of $x(t)$ in the limit of $t \rightarrow \infty$ as

$$\begin{aligned} P(\ge x)=2\{1+(g-1)x \}^{-\frac{\log (2)}{\log (g)}}, \end{aligned}$$

(17)

where $P( \ge x)$ denotes the probability that $x(\infty )$ takes a value larger than or equal to $x$. In the case in which $g>1$ we have the asymptotic power-law distribution for very large value of $x$,

$$\begin{aligned} P(>x) \propto x^{-\alpha } , \end{aligned}$$

(18)

where the exponent $\alpha =\log (2)/\log (g)$ fulfils Eq. (3) in the range $0<\alpha <\infty$, namely,

$$\begin{aligned} \langle g(t)^\alpha \rangle =\frac{1}{2}\cdot g^{\alpha }+\frac{1}{2}\cdot 0=1. \end{aligned}$$

(19)

With this special example, we confirm the validity of Eqs. (1)–(3). Note that, in this example, the stationary condition, $\langle \log (g(t))\rangle <0$, is automatically satisfied because the condition that $g(t)=0$ with probability $1/2$ gives the value $\langle \log (g(t))\rangle =-\infty$.

The key point of realising the power law in this multiplicative random process is understood intuitively by neglecting the additive term. The probability of repeating $g(t)=g$ for $k$ time steps is given as $p(k) \equiv 1/2^k= e^{-k\log (2)}$ and the corresponding value of $x(t)$ is approximated as $x(t) \approx g^k=e^{k\log (g)}$; then by deleting $k$ from these relations we have Eq. (18). Namely, successive exponential growth with an exponential distribution of duration time gives the power-law distribution.

This type of power-law derivation can be generalised in the following way. Let us consider the following general form of a random multiplicative process:

$$\begin{aligned} x(t+\Delta t)=g(t)x(t)+f(t), \end{aligned}$$

(20)

where $g(t)$ and $f(t)$ are independent random variables taking positive values, and we assume the situation in which $\log g(t)$ fluctuates around $0$ [41]. By taking the logarithm of both sides and introducing variables $y(t) \equiv \log {(x(t))}$ and $r(t)=\log g(t)$, Eq. (20) can be transformed as

$$\begin{aligned} y(t+\Delta t)=\log {\{g(t)x(t)+f(t)\}}=y(t)+r(t)+\frac{f(t)}{g(t)x(t)}+\cdots . \end{aligned}$$

(21)

By neglecting the terms including $f(t)$ as higher order terms, the time evolution of the probability density of $y(t)$, $p(y,t)$, is approximated by a Fokker-Plank equation,

$$\begin{aligned} p(y,t+\Delta t) \approx \int ^{\infty }_{-\infty } \omega (r) p(y-r,t)dr =p(y,t)-\langle r\rangle \frac{\partial p(r,t)}{\partial y}+\frac{\langle r^2\rangle }{2}\frac{\partial ^2 p(r,t)}{\partial ^2 y}+\cdots , \end{aligned}$$

(22)

where $\omega (r)$ denotes the probability density of $r$. Assuming the existence of a statistically steady state, we have the following exponential distribution:

$$\begin{aligned} p(y) \propto \exp ^{\frac{2\langle r\rangle }{\langle r^2\rangle }y} . \end{aligned}$$

(23)

In the situation, $\langle r\rangle =\langle \log (g)\rangle <0$, which is equivalent to the condition of the existence of a steady state for a random multiplicative process [19], Eq. (23) is shown to be equivalent to the power law of Eq. (18), with its exponent given as

$$\begin{aligned} \alpha \approx -\frac{2\langle r\rangle }{\langle r^2\rangle } . \end{aligned}$$

(24)

This value is derived from the exact relation, Eq. (3). Expanding the left-hand side of the equation, $\langle g(t)^\alpha \rangle =1$, in terms $\alpha$ and equating the second and third terms on the right-hand side as an approximation lead to

$$\begin{aligned} \langle g(t)^\alpha \rangle&= \langle e^{\alpha \log (g(t))}\rangle \nonumber \\&= 1+\alpha \langle \log ( g(t) )\rangle + \alpha ^2 \frac{\langle \{\log (g(t))^2\}\rangle }{2}+\cdots . \end{aligned}$$

(25)

The key equation for determining the value of the exponent, Eq. (3), can be derived roughly in the following way. Neglecting the additive term on the right-hand side of Eq. (20) and taking an average over realisations after taking the $s$th power of both sides, we have the following relation:

$$\begin{aligned} \langle x(t+\Delta t)^s\rangle \approx \langle g(t)^s\rangle \langle x(t)^s\rangle . \end{aligned}$$

(26)

For $\langle g(t)^s\rangle > 1$ it is clear that $\langle x(t)^s\rangle$ diverges in the limit of $t \rightarrow \infty$. However, if $\langle g(t)^s\rangle <1$ the value of $\langle x(t)^s\rangle$ is always finite. Therefore, we have the following relations:

$$\begin{aligned} \langle x(\infty )^s\rangle = \left\{ \begin{array}{ll} \infty &{} (s >\alpha ), \\ \text {finite} &{} ( s< \alpha ), \\ \end{array} \right. \end{aligned}$$

(27)

where $\alpha$ satisfies Eq. (3). This property of Eq. (27) is a typical characteristic of the power-law distribution, Eq. (18). Therefore, we can find that the power-law exponent in Eq. (18) is consistent with Eq. (3). Note that Solomon et al. elaborated on a generalised version of this type of model, $x(t+1)=g(t)f_1(x(t))+f_2(x(t))$, where both $f_1$ and $f_2$ are nonlinear functions, and they derived the relationship between the exponents and these functions [39].

A rigorous mathematical derivation of this relation was done by Kesten in 1973 using a more general form of a real-valued matrix by considering also the case in which the distribution of the additive noise follows a power law [19]. In his proof the value of $\alpha$ is limited to the range $0 < \alpha \le 2$ as he applies the theory of stable distributions; however, our numerical analysis and the above intuitive theoretical analysis suggest that the value of $\alpha$ can be extended to the whole range $0< \alpha$.

It should be noted that the existence of the additive term in Eq. (1) or Eq. (20) is essential to realise the statistically steady state. As known from Eq. (21), the stochastic process is a random walk with a negative trend in view of $\log (x(t))$; therefore, without any additive noise term the random walker tends to shrink to $x(t)=0$, which is not the power-law steady state. Even without the additive term ($f(t) \equiv 0$) the same power-law steady state can also be realised by introducing a repulsive boundary condition, such as requiring $x(t) \ge 1$ for Eq. (20) by adding a rule that $x(t+\Delta t)=1$ when $x(t)<1$.

Dividing both sides of Eq. (20) by $\Delta t$ and considering the continuum limit of $\Delta t \rightarrow 0$, we have the following Langevin equation with a time-dependent viscosity:

$$\begin{aligned} \frac{d}{dt}X(t)=-\mu (t)X(t)+F(t) , \end{aligned}$$

(28)

where

$$\begin{aligned} X(t) \equiv x(t), \quad \mu (t) \equiv \lim _{\Delta t \rightarrow \infty }\frac{1-g(t)}{\Delta t}, \quad F(t) \equiv \lim _{\Delta t \rightarrow \infty }\frac{f(t)}{\Delta t}. \end{aligned}$$

(29)

As known from this equation, the case of $g(t)>1$ corresponds to a negative value of viscosity ($\mu (t)<0$). In the case of a colloidal particle’s diffusion in water such a negative viscosity cannot be realised; however, in the case of voltage fluctuation in an electric circuit, which is approximated also by a Langevin equation, we can consider a negative viscosity state by introducing an amplifier into the circuit. Namely, the value of $\mu (t)$ corresponds to resistivity in the electric circuit and in the situation in which fluctuation of voltage is amplified as a whole, and the effective resistivity takes a negative value. By introducing an electric circuit in which an amplifier works at random timing, we have a physical situation that is described by Eq. (28) and power-law distributions of voltage fluctuation are confirmed experimentally [36].

Appendix B: Basic Properties of the Moment Function

Because Eq. (3) is key to determining the exponent of the power law of Eq. (2), $\alpha$, here, we summarise the basic properties of the moment function for the growth rate of a subunit, $M(s) \equiv \langle g_j(t)^s\rangle$. This is a continuous function and it is concave with respect to $s$ for any distribution of $g_j(t)$ because the second derivative of this function is always positive: $M(s)'' \equiv \langle (\log (g_j(t))^2g_j(t)^s\rangle >0$. Because $M(0)=1$ is an identity, if $M(\alpha )=1$ holds for a positive value of $\alpha$, then we know that $M(s)<1$ for $0<s<\alpha$ and $M(s)>1$ for $\alpha <s,$ as schematically shown in Fig. 6. So, $M(2) < 1$ corresponds to $2< \alpha ,$ as shown in the first column of Table 1. In the situation in which Eq. (3) holds with $0 < \alpha <1$, then we have $M(1)=\langle g_j(t)\rangle >1$, whereas in the situation for which $1<\alpha$, we have $M(1)=\langle g_j(t)\rangle <1$.

The stationary condition, $\langle \log (g(t))\rangle < 0$, means that the slope at the origin, $M(0)'$, is negative, so if this condition is not fulfilled $M(s)>1$ for any positive $s$, implying that the stochastic process of Eq. (1) is not stationary. In contrast, if the probability of occurrence of $g_j(t) > 1$ is $0$, it is trivial that $M(s) < 1$ for any positive $s$. Reference [23] provides more details and addresses applications to financial bubbles.

Fig. 6

Schematic graph of the moment function

Appendix C: Brief Review of the Generalised Central Limit Theorem

The central limit theorem is one of the most powerful mathematical tools; however, it is used too often to approximate the sum of random variables, of the form $Y(N) \equiv y_1+y_2+\cdots +y_N$, by normal distributions. In fact, there are three required conditions on random variables for their sums to obey the central limit theorem [10]:

• 1. All random variables must follow an identical distribution.

• 2. The variables must be independent.

• 3. The variance of the variables must be finite.

If one of these conditions is violated, then the central limit theorem does not apply.

Violation of the first condition has recently been attracting attention as super-statistics, that is, superposition of stochastic variables having different statistics [5]. As an old example, a fat-tailed velocity distribution observed in randomly stirred granular particles can be explained by superposition of normal distributions having different variances owing to clustering caused by inelastic collisions [45]. Giving a general discussion of correlated variables violating the second condition is rather difficult, as the details depend on the details of correlation. It is known that universal properties independent of the details of the system can be expected at the critical point of a phase transition at which power-law distributions and power-law scaling relations play important roles [42]. Further, theoretical approaches based on the concept of “nonextensive entropy” can provide general solutions for strongly correlated systems having scale-free interactions such as charged particles [14]. However, when one considers activity of a business firm, for example, it seems very difficult to describe both internal and external interactions by a general mathematical formulation.

Violation of the third condition, infinite variance, was intensively studied in the 1930s by the pioneering mathematician P. Levy as “stable distributions” [22]. Assuming that $\{z_1,z_2,\dots ,z_N\}$ are independent identically distributed random variables, he showed that the fluctuation width of the sum $Z_N$ increases proportional to $N^{1/\alpha }$ in general, where $\alpha$ is called the characteristic exponent and lies in the range $0<\alpha \le 2$. The limit distribution is defined for the normalised variable, $z \equiv \{Z_N-A_N\}N^{-1/\alpha }$ , where $A_N$ is a term corresponding to the mean value. In the limit of $N \rightarrow \infty$, the distribution of $z$ becomes a stable distribution that has a power-law tail $p(z)\propto z^{-\alpha -1}$ for $0<\alpha <2$. The limit distribution converges to the normal distribution when $\alpha =2$, according to the ordinary central limit theorem. This general result is called the generalised central limit theorem (GCLT). The general functional form of the stable distribution is given by Eqs. (12) and (13) [10].

1.1 C.I: The Domain of Attraction of the Generalised Central Limit Theorem

Here, we review the domains of attraction of the GCLT more precisely [51]. We consider the scaled sum of random variables,

$$\begin{aligned} Z_N=\frac{1}{B_N}\left( \sum ^{N}_{i=1}z_i-A_N\right) \!, \end{aligned}$$

(30)

where $A_N$ and $B_N$ are sequences, as discussed later, and we assume that $z_i$ has the PDF satisfying the following conditions:

$$\begin{aligned} P_{z}(x) \approx c^{+} \cdot \lambda \cdot x^{-\lambda -1} \quad (x \rightarrow \infty ) \quad (j=1,2,\dots ,N) , \end{aligned}$$

(31)

$$\begin{aligned} P_{z}(x) \approx c^{-} \cdot \lambda \cdot |x|^{-\lambda -1} \quad (x \rightarrow -\infty ) \quad (j=1,2,\dots ,N), \end{aligned}$$

(32)

where $c^{+}$, $c^{-}$, and $\lambda$ are positive constants and $P_{z}(x)$ are the PDFs of $z_j$ ($j=1,2,\dots ,N$). According to the GCLT, $Z_N$ observes a stable distribution with the parameters

$$\begin{aligned} \alpha ={\left\{ \begin{array}{ll} \lambda &{} (\lambda \le 2), \\ 2 &{} (\lambda >2), \end{array}\right. } \end{aligned}$$

(33)

and

$$\begin{aligned} \beta =\frac{c^{+}-c^{-}}{c^{+}+c^{-}}. \end{aligned}$$

(34)

Here, the characteristic function of the stable distribution is defined as

$$\begin{aligned} \phi (z;\alpha ,\beta ,\gamma ,\delta )=\exp \left[ i \delta z-{( \gamma |z| )}^{\alpha } \left\{ 1+i\beta \frac{z}{|z|}\omega (z,\alpha )\right\} \right] ,\end{aligned}$$

(35)

$$\begin{aligned} \omega (z,\alpha )=\left\{ \begin{array}{l} \tan (\frac{\pi \alpha }{2}) \quad (\alpha \ne 1),\\ \frac{2}{\pi }\log (z) \quad (\alpha =1),\\ \end{array} \right. \end{aligned}$$

(36)

and the coefficients $A_N$ and $B_N$ were defined as

$$\begin{aligned} A_N= {\left\{ \begin{array}{ll} 0 &{} (0 < \lambda < 1 ), \\ \beta \cdot (c^{+}+c^{-}) \cdot N \cdot \log (N) &{} (\lambda =1), \\ N \cdot \langle z\rangle &{} (\lambda >1), \\ \end{array}\right. } \end{aligned}$$

(37)

$$\begin{aligned} B_N= {\left\{ \begin{array}{ll} \,[\pi (c^{+}+c^{-})]^{1/\alpha }\cdot [2\varGamma (\alpha )\sin (\alpha \pi /2)]^{-1/\alpha } \cdot N^{1/\alpha } &{} (0 < \lambda < 1 ), \\ (\pi /2) \cdot (c^{+}+c^{-}) \cdot N &{} (\lambda =1), \\ \,[\pi (c^{+}+c^{-})]^{1/ \alpha }[2 \varGamma ( \alpha ) \sin ( \alpha \pi /2)]^{-1/ \alpha } \cdot N^{1/ \alpha } &{} (1 < \lambda < 2),\\ (c^{+}+c^{-})^{1/2}[N\log (N)]^{1/2}&{}(\lambda =2), \\ \,[(1/2)\langle (x-\langle x\rangle )^2\rangle ^{1/2}] \cdot N^{1/2} &{}(\lambda > 2). \end{array}\right. } \end{aligned}$$

(38)

Appendix D: Growth Rate of the System for $\alpha \ge 1$

We calculate the growth rate $G(t;N)$ using the GCLT in the case in which the distribution converges to a stable distribution. Here, we assume that

$$\begin{aligned} x_j(t+1)=g_j(t)x_j(t)+f_j(t) \quad (j=1,2,\dots ,N) \end{aligned}$$

(39)

and for the steady state

$$\begin{aligned} P_{x_j}(x) \approx d_g \cdot \alpha _g \cdot x^{-\alpha _g-1} \quad (x \rightarrow \infty ) \quad (j=1,2,\dots ,N) , \end{aligned}$$

(40)

where $d_g$ is the constant determined by the PDF of $g_j$, $P_{g}(g)$, and $\alpha _g$ satisfies $\langle g_j(t)^{\alpha _g}\rangle =1$.

1.1 D.I: $\alpha _g > 1$

First, we investigate the case of $\alpha _g>1$, namely, where the mean of $g_j$ takes a value less than $1$.

Considering the domain of attraction of the GCLT, as given in Appendix C, we transform $G(t;N)$ for the steady state as follows:

$$\begin{aligned} G_N&= \frac{\sum ^{N}_{j=1}g_j x_j}{\sum ^{j=1}_{N}x_j} =\langle g\rangle +\frac{1}{N} \cdot \frac{B_N^{(1)}J_1}{\left( B_N^{(2)}/N\right) J_2+\langle x\rangle }, \end{aligned}$$

(41)

where $G_N$ is the growth rate for the steady state, $G_N \equiv G(t;N) \; (t \rightarrow \infty )$,

$$\begin{aligned} \langle g\rangle&\equiv \langle g_j\rangle \quad (i=1,2,\dots ,N), \end{aligned}$$

(42)

$$\begin{aligned} \bar{g}_j&\equiv g_j-\langle g\rangle , \end{aligned}$$

(43)

$$\begin{aligned} \zeta _j&\equiv \bar{g}_j \cdot x_j, \end{aligned}$$

(44)

$$\begin{aligned} J_1&\equiv \frac{\sum _{j=1}^{N}\zeta _j}{B_N^{(1)}} ,\end{aligned}$$

(45)

$$\begin{aligned} J_2&\equiv \frac{\sum _{j=1}^{N}x_j-N\langle x\rangle }{B_N^{(2)}} ,\end{aligned}$$

(46)

$$\begin{aligned} B_N^{(1)}&\equiv {\left\{ \begin{array}{ll} N^{1/\alpha _g} \cdot (c_1^{+}+c_1^{-})^{1/\alpha _g} \cdot F(\alpha _g) &{} (1 <\alpha _g < 2), \\ (N\log (N))^{1/2} \cdot (c_1^{+}+c_1^{-})^{1/2} &{} (\alpha _g =2), \\ N^{1/2} \cdot (1/2\langle (gx-\langle gx\rangle )^2\rangle )^{1/2} &{} (\alpha _g >2), \end{array}\right. }\end{aligned}$$

(47)

$$\begin{aligned} B_N^{(2)}&\equiv {\left\{ \begin{array}{ll} N^{1/\alpha _g} \cdot (c_2^{+}+c_2^{-})^{1/\alpha _g} \cdot F(\alpha ) &{} (1 <\alpha _g < 2), \\ (N\log (N))^{1/2} \cdot (c_2^{+}+c_2^{-})^{1/2} &{} (\alpha _g =2), \\ N^{1/2} \cdot (1/2\langle (x-\langle x\rangle )^2\rangle )^{1/2} &{} (\alpha _g>2), \end{array}\right. }\end{aligned}$$

(48)

$$\begin{aligned} F(\alpha )&\equiv [1/\pi \cdot 2 \varGamma (\alpha )\sin (\alpha \pi /2)]^{-1/\alpha }, \end{aligned}$$

(49)

and

$$\begin{aligned} c_1^{+}&\equiv \lim _{y \rightarrow \infty }(1/\alpha _g) y^{\alpha _g+1} P_{\zeta _j}(y), \end{aligned}$$

(50)

$$\begin{aligned} c_1^{-}&\equiv \lim _{y \rightarrow -\infty }(1/\alpha _g) |y|^{\alpha _g+1} P_{\zeta _j}(y), \end{aligned}$$

(51)

$$\begin{aligned} c_2^{+}&\equiv \lim _{y \rightarrow \infty }(1/\alpha _g) y^{\alpha _g+1} P_{x_j}(y) ,\end{aligned}$$

(52)

$$\begin{aligned} c_2^{-}&\equiv \lim _{y \rightarrow -\infty }(1/\alpha _g) |y|^{\alpha _g+1} P_{x_j}(y). \end{aligned}$$

(53)

Because $B_N^{(2)}/N \rightarrow 0$ ($N \rightarrow \infty$), we can neglect the term $B_N^{2}/N \cdot J_2$ in the denominator of Eq. (41) for $N\gg 1$, and we obtain the approximation

$$\begin{aligned} G_N \approx \langle g\rangle +\frac{B_N^{(1)}}{N} \cdot \frac{J_1}{\langle x\rangle }. \end{aligned}$$

(54)

From the GCLT, $J_1$ observes a stable distribution with the parameters $\alpha =\alpha _g$, $\beta =(c_1^{+}-c_1^{-})/(c_1^{+}+c_1^{-})$, $\gamma =1,$ and $\delta =0$, where the characteristic function of the stable distribution is defined as Eq. (35).

Next, we specify $c_1^{+}$, $c_1^{-}$, $c_2^{+}$, and $c_2^{-}$. By applying the formula of the transformation of random variables to $\zeta _j=b_jx_j$,

$$\begin{aligned} P_{(\zeta )}(z)=\int _{\zeta _{min}}^{\zeta _{max}}\frac{1}{|\bar{g}|} P_{\bar{g}}(g) \cdot P_x(z/\bar{g})dg, \end{aligned}$$

(55)

where $\zeta _{min}=\text {max}\{g_{min}-\langle g\rangle \}$, $\min \{z/x_{min},0\}\}$, $\zeta _{max}=\text {min}\{g_{max}-\langle g\rangle ,\text {max}\{z/x_{min},0\}\}$, the support of the PDF of $g_j$ is $[g_{min}, g_{max}]$ and the support of the PDF of $x_j$ is $[x_{min}, \infty ]$.

Taking the limit of $z$ gives

$$\begin{aligned} P_{(\zeta )}(z) ={\left\{ \begin{array}{ll} |z|^{-\alpha _g-1} \cdot d_g \cdot \alpha _g \int _{g_{min}-\langle g\rangle }^{0}p_{\bar{g}}(g) \cdot |\bar{g}|^\alpha _g d\bar{g} &{} (z \rightarrow -\infty ), \\ |z|^{-\alpha _g-1} \cdot d_g \cdot \alpha _g \int ^{g_{max}-\langle g\rangle }_{0}p_{\bar{g}}(g) \cdot |\bar{g}|^\alpha _g d\bar{g} &{} (z \rightarrow \infty ). \end{array}\right. } \end{aligned}$$

(56)

Thus,

$$\begin{aligned} c_{1}^{+}&= d_g \cdot \int _{g_{min}-\langle g\rangle }^{0}p_{\bar{g}}(g) \cdot |\bar{g}|^\alpha _g d_g \bar{g} ,\end{aligned}$$

(57)

$$\begin{aligned} c_{1}^{-}&= d_g \cdot \int ^{g_{max}-\langle g\rangle }_{0}p_{\bar{g}}(g) \cdot |\bar{g}|^\alpha _g d_g \bar{g} . \end{aligned}$$

(58)

In addition, from Eq. (40),

$$\begin{aligned} c_{2}^{+}&= d_g ,\end{aligned}$$

(59)

$$\begin{aligned} c_{2}^{-}&= 0. \end{aligned}$$

(60)

As a result, $G_N$ observes a stable distribution with the parameters

$$\begin{aligned}&\alpha = {\left\{ \begin{array}{ll} \alpha _g &{} (1 < \alpha _g <2), \\ 2 &{} (\alpha _g \ge 2), \end{array}\right. }\end{aligned}$$

(61)

$$\begin{aligned}&\beta =\frac{c_1^{+}-c_1^{-}}{c_1^{+}+c_1^{-}}=\frac{\langle (g-\langle g\rangle )(|g-\langle g\rangle |)^{\alpha -1}\rangle }{\langle (|g-\langle g\rangle |)^\alpha \rangle } ,\end{aligned}$$

(62)

$$\begin{aligned}&\gamma =\frac{B_N^{1}}{N\langle x\rangle }= {\left\{ \begin{array}{ll} N^{1/\alpha -1} \cdot (\langle (|g-\langle g\rangle |)^\alpha \rangle )^{1/\alpha } \cdot F(\alpha ) \cdot d_g/\mu _x &{} (1 <\alpha _g < 2), \\ N^{-1/2} \cdot \log (N)^{1/2} \cdot (|g-\langle g\rangle |^\alpha )^{1/2} \cdot d_g/\mu _x &{} (\alpha _g =2), \\ N^{1/2} \cdot 1/\sqrt{2} \cdot \sigma _{\zeta }/\mu _x &{} (\alpha _g>2), \end{array}\right. } \end{aligned}$$

(63)

where $\mu _x \equiv \langle x\rangle =\langle f\rangle /(1-\langle g\rangle )$ and $\sigma _{\zeta } \equiv \langle \{(g-\langle g\rangle )x\}^2>^{1/2}=\big [\langle (g-\langle g\rangle )^2\rangle \cdot \{(\langle (f-\langle f\rangle )^2\rangle +\mu _x^2 \cdot \langle (g-\langle g\rangle )^2\rangle )/(1-\langle g^2\rangle )+\mu _x^2\}\big ]^{1/2}$.

1.2 D.II: $\alpha _g = 1$

In the same manner as was done for the case of $\alpha _g>1$, we calculate the case of $\alpha _g=1$, namely, where $\langle g_j\rangle =1$. Considering the domain of attraction of the GCLT given in Appendix C, we transform the expression of the growth rate of the system for the steady state, $G_N$,

$$\begin{aligned} G_N&= \frac{\sum ^{N}_{j=1}g_j \cdot x_j}{\sum ^{j=1}_{N}x_j} \end{aligned}$$

(64)

$$\begin{aligned}&= \langle g\rangle +\frac{1}{N \log (N)} \cdot \frac{B_N^{(1)} \cdot J_1+N\log (N)\cdot \beta _1 (c_1^{+}+c_1^{-})}{B_N^{(2)}/\{N \log (N)\} \cdot J_2+\beta _2 (c_2^{+}+c_2^{-}) }, \end{aligned}$$

(65)

where

$$\begin{aligned} \langle g\rangle&\equiv \langle g_j\rangle \quad (i=1,2,\dots ,N), \end{aligned}$$

(66)

$$\begin{aligned} \zeta _j&\equiv (g_j-\langle g\rangle ) \cdot x_j, \end{aligned}$$

(67)

$$\begin{aligned} J_1&\equiv \frac{\sum _{j=1}^{N}\zeta _j-N \cdot \log (N) \cdot \beta _1 \cdot (c_1^{+}+c_1^{-})}{B_N^{(1)}} ,\end{aligned}$$

(68)

$$\begin{aligned} J_2&\equiv \frac{\sum _{j=1}^{N}x_j-N \cdot \log (N) \cdot \beta _1 \cdot (c_1^{+}+c_1^{-})}{B_N^{(2)}} ,\end{aligned}$$

(69)

$$\begin{aligned} B_N^{(1)}&\equiv (\pi /2)(c_1^{+}+c_1^{-})N = (\pi /2) d_g\langle |g-\langle g\rangle |\rangle \ \cdot N ,\end{aligned}$$

(70)

$$\begin{aligned} B_N^{(2)}&\equiv (\pi /2)(c_2^{+}+c_2^{-})N = (\pi /2) d_g \cdot N,\end{aligned}$$

(71)

$$\begin{aligned} \beta _1&= \frac{c_1^{+}-c_1^{-}}{c_1^{+}+c_1^{-}}=\frac{\langle (g-\langle g\rangle )\rangle }{\langle |g-\langle g\rangle |\rangle }=0,\end{aligned}$$

(72)

$$\begin{aligned} \beta _2&= \frac{c_2^{+}-c_2^{-}}{c_2^{+}+c_2^{-}}=\frac{d-0}{d-0}=1 . \end{aligned}$$

(73)

Because $B_N^{(2)}/(N\log (N)) \propto 1/\log (N) \rightarrow 0$ ($N \rightarrow \infty$), roughly, we can neglect the $B_N^{(2)}/(N \log (N)) \cdot J_2$ term in the denominator for $N\gg 1$. Then we obtain the following approximation:

$$\begin{aligned} G_N \approx \langle g\rangle +\frac{B_N^{(1)}}{N \cdot \log (N)} \cdot \frac{J_1}{d_g}. \end{aligned}$$

(74)

From the GCLT and the properties of a stable distribution, $G_N$ observes a stable distribution with the parameters

$$\begin{aligned} \alpha&= 1, \end{aligned}$$

(75)

$$\begin{aligned} \beta&= \beta _1=\frac{\langle (g-\langle g\rangle )(|g-\langle g\rangle |)^{\alpha _g-1}\rangle }{\langle (|g-\langle g\rangle |)^{\alpha _g}\rangle }=0, \end{aligned}$$

(76)

$$\begin{aligned} \gamma&= \frac{1}{\log (N)} \cdot \frac{\pi }{2} \cdot \frac{d_g \langle |g-\langle g\rangle |\rangle }{d_g}=\frac{\pi }{2} \cdot \frac{1}{\log (N)} \cdot \langle |g-1|\rangle , \end{aligned}$$

(77)

$$\begin{aligned} \delta&= \langle g\rangle =1. \end{aligned}$$

(78)

This distribution is equivalent to the Cauchy distribution with the following parameters:

$$\begin{aligned} \mu&= 1,\end{aligned}$$

(79)

$$\begin{aligned} \sigma _N&= \frac{\pi }{2} \cdot \frac{1}{\log (N)} \cdot \langle |g-1|\rangle , \end{aligned}$$

(80)

where the Cauchy distribution is defined as

$$\begin{aligned} f_{c}(G_N;\mu ,\sigma _N)=\frac{1}{\pi } \cdot \frac{\sigma _N}{(G_N-\mu )^2+\sigma _N^2}. \end{aligned}$$

(81)

Appendix E: Scaling of the Variance of the Model

In Ref. [54], it is reported that the scaling of the variance (or the standard deviation) is different from that of the PDF of the growth rates. In an analogous way, we investigate the scaling of the variance of our model.

Theoretical approximation. Here, we assume that the distribution of the unit growth rates $g_i$ have the support $[0,g_{max}]$. It is trivial that $G_N \le g_{max}$. The variance of $G_N$ is written as

$$\begin{aligned} \langle (G_N-\langle G_N\rangle )^2\rangle&= \int _{0}^{g_{max}}(G_N-\langle G_N\rangle )^2 \cdot P_{G_N}(G_N) \cdot dG_N. \end{aligned}$$

(82)

For large $N$, the PDF of the system growth rate, $P_{G_N}(G_N),$ is approximated by the stable distribution with the parameters given by Eqs. (61), (62), (63), and (80). On this condition, the asymptotic tail behaviour of the PDF is approximated as [51]

$$\begin{aligned} P_{G_N}(G_N) \approx \frac{1}{2} \cdot \alpha \cdot \left( 1+\beta \cdot \frac{G_N-\langle g_i\rangle }{|G_N-\langle g_i\rangle |}\right) \cdot |G_N-\langle g_i\rangle |^{-\alpha -1} \cdot N^{1-\alpha }. \end{aligned}$$

(83)

Since the contribution of the central part of the PDF to the variance is much smaller than that of the tail part of the PDF (i.e. the power-law part) for large $N$, we neglect the central part. Then we obtain

$$\begin{aligned} \langle (G_N-\langle G_N\rangle )^2\rangle&\approx \int _{0}^{\langle g_i\rangle -\epsilon }(\bar{G}_N)^2 \cdot \frac{1}{2} \cdot \alpha \cdot \left( 1+\beta \cdot \frac{\bar{G}_N}{|\bar{G}_N|}\right) \cdot N^{1-\alpha } \cdot |\bar{G}_N|^{-\alpha -1} \cdot dG_N,\qquad \end{aligned}$$

(84)

$$\begin{aligned}&+ \int _{\langle g_i\rangle +\epsilon }^{g_{max}}(\bar{G}_N)^2 \cdot \frac{1}{2} \cdot \alpha \cdot \left( 1+\beta \cdot \frac{\bar{G}_N}{|\bar{G}_N|}\right) \cdot N^{1-\alpha } \cdot |\bar{G}_N|^{-\alpha -1} \cdot dG_N \qquad \end{aligned}$$

(85)

$$\begin{aligned}&\propto N^{1-\alpha } , \end{aligned}$$

(86)

where $\bar{G}_N \equiv G_N-\langle g_i\rangle$. Therefore, the scaling of the standard deviation of the system growth rate is $\propto N^{(1-\alpha )/2}$. This scaling is different from the scaling of the scale parameter of the stable distribution $N^{1-1/\alpha }$.

Numerical confirmation. We confirm the above-mentioned result numerically. We calculate $G(t;N)$ for the following condition:

$$\begin{aligned} g_i(t)= {\left\{ \begin{array}{ll} 0 &{} \text {(prob 0.5),} \\ g_0 &{} \text {(prob 0.5}), \\ \end{array}\right. } \end{aligned}$$

(87)

where $\langle g_i^\alpha \rangle =1$, namely, $g_0=2^{1/\alpha }$, and

$$\begin{aligned} f_i(t)= {\left\{ \begin{array}{ll} 1, &{} x_i(t)< 1, \\ 0, &{} x_i(t) \ge 1. \\ \end{array}\right. } \end{aligned}$$

(88)

For very large $N$, we transform $G_N$ as follows:

$$\begin{aligned} G_N&= \frac{\sum ^{N}_{i=1}g_i \cdot x_i}{\sum ^{N}_{i=1}x_i} \end{aligned}$$

(89)

$$\begin{aligned}&= \frac{g_0 \cdot \sum _{i \in \{i|g_i=g_0\}}x_i}{\sum _{i \in \{i| g_i=g_0\}}x_i+\sum _{i \in \{i|g_i=0\}}x_i} \end{aligned}$$

(90)

$$\begin{aligned}&= \frac{g_0 \cdot S_a}{S_a+S_b}, \end{aligned}$$

(91)

where

$$\begin{aligned} S_a&\equiv \sum _{i \in \{i|g_i=g_0\}}x_i\end{aligned}$$

(92)

$$\begin{aligned} S_b&\equiv \sum _{i \in \{i|g_i=0\}} x_i. \end{aligned}$$

(93)

For $N\gg 1$, $S_a$ and $S_b$ can be approximated by a stable distribution with the parameters $\alpha =\alpha _g$, $\beta =1$, $\gamma =(N/2)^{1/\alpha _g} \cdot F(\alpha _g)$, and $\delta =N/2 \cdot \langle x_i\rangle$ because $\sum _{i \in \{i|g_i=g_0\}}1 \sim \sum _{i \in \{i|g_i=0\}}1 \sim N/2$ and $x_i$ observes the following power-law distribution:

$$\begin{aligned} p_{x_i}(x_i)&= \alpha _g \cdot x_i^{-\alpha _g-1}. \end{aligned}$$

(94)

We apply this approximation for calculations of $G_N$ in this section.

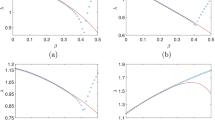
Fig. 7a and b illustrate the standard deviation and the IQR of the system growth rate $G_N$. From the black triangle in the figure, we confirm that the standard deviation is in accordance with the theoretical result $N^{(1-\alpha )/2}$ given by Eq. (86) in the case of $\alpha _g=1.5$, namely, $g^{1/1.5}=1$ for $N<10^{11}$ and Eq. (86) holds for all $N$ in the case of $\alpha _g=1.06$.

Fig. 7

Comparison of the standard deviation and the IQR for the growth rate $G_N$. The black triangles indicate the standard deviation and the green squares indicate the IQR. a $\alpha _g=1.5;$ b $\alpha _g=1.06$; red dashed lines are proportional to $N^{(1-\alpha _g)/2}$ and blue dash dotted lines are proportional to $N^{1-1/\alpha _g}$. c The difference between the maximum sample of $G_N$ and the mean of $G_N$ for $\alpha _g=1.5$ and d the corresponding figure in the case of $\alpha _g=1.06$ (Color figure online)

Note that in the case of $\alpha _g=1.5$ shown in Fig. 7a, for $N>10^{11}$, the standard deviation is proportional to $N^{1-1/\alpha _g}$, whose exponent is closer to that of the IQR. What causes this transition of the scaling exponent from $(1-\alpha _g)/2$ to $1/\alpha _g-1$ is the finite-size effect for the sample number. In a finite sample, the maximum values of the asymptotic stable distribution, $g_{stable}$, are estimated at $N^{1-/\alpha _g}\cdot m^{1/\alpha _g}$ for $\alpha _g<1$ and $1/\log (N) \cdot m^{1/\alpha }$ for $\alpha _g=1$ by using the extreme value theory [15], where we denote the sample number as $m$ (i.e. we apply $m=10^5$ in the simulation.). We can neglect the cutoff of $g_{max}$ on the condition $g_{stable}\ll g_{max}$, namely, $N^{1-/\alpha _g}\cdot m^{1/\alpha _g} \ll g_{max}$ for $1<\alpha _g<2$ or $1/\log (N) \cdot m^{1/\alpha _g} \ll g_{max}$ for $\alpha _g=1$. Therefore, the standard deviation observes the scaling $N^{1-1/\alpha _g}$ for $N\gg m$. In fact, from Figs. 7c and d, we can confirm that the maximum value of the samples of $G_N$ approximately equals $g_{max}$ for the case in which the standard deviation follows the scaling $N^{(1-\alpha _g)/2}$, namely, the case when $N<10^{11}$ for $\alpha _g=1.5$ and in the case of any $N$ for $\alpha _g=1.06$. We should also note that the above-mentioned conditions that the scalings of the standard deviation are consonant with the scalings of the IQR (i.e. $\propto N^{1-1/\alpha }$ for $\alpha \ge 1$ or $\propto 1/\log (N)$ for $\alpha >1$) are associated with the condition that the denominator of Eq. (41) can be approximated by $\langle x\rangle$ even with fluctuations considered, as $\langle x\rangle$ is sufficiently larger than the maximum value of $B_N^{(2)}/N \cdot J_2$ for a given sample number $m$. In particular, in the case of $1<\alpha _g<2$, the condition that the standard deviation observes $N^{1-1/\alpha _g}$ is given by the condition $g_{stable} \approx N^{1-/\alpha _g}\cdot m^{1/\alpha _g} \ll g_{max}=\text {const}.,$ as already discussed above. Conversely, the condition that the denominator of Eq. (41) can be approximated by $\langle x\rangle$ is given by the condition $N^{1-1/\alpha _g} \cdot m^{1/\alpha }\ll \langle x\rangle =\text {const}$. To approximate the maximum value of $J_2$, we use the approximation of $m$ samples for power-law random variables with the exponent $\alpha$ as $\{m^{1/\alpha },(m/2)^{1/\alpha },(m/3)^{1/\alpha },\dots ,1\}$. From these calculations, we can confirm that both conditions are in accordance with the functional form of $N$. The same discussion is applicable also for the case $\langle \alpha \rangle =1$.